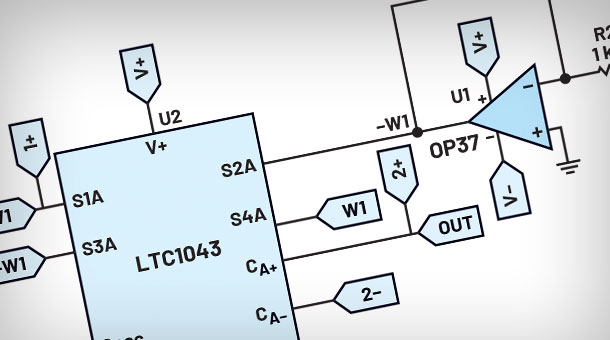
学子专区论坛— 文氏电桥振荡器的 分析与制作(第二部分):实现方案
欢迎大家。如果您是一名电气工程专业学生或对模拟电子技术感兴趣的应届毕业生,只需单击或双击即可查看文章、教程和大量其它有用资源。

ADALM2000 Activity: An Ohm‘s Law Experiment
by Antoniu Miclaus

学子专区—文氏电桥振荡器的 分析与制作(第二部分):实现方案
by Mark Thoren
更多学生专区文章
过往期刊
 卷 57, 3
卷 57, 3 卷 57, 2
卷 57, 2 卷 57, 1
卷 57, 1 卷 56, 4
卷 56, 4 卷 56, 3
卷 56, 3 卷 56, 2
卷 56, 2 卷 56, 1
卷 56, 1 卷 55, 4
卷 55, 4 卷 55, 3
卷 55, 3 卷 55, 2
卷 55, 2 卷 55, 1
卷 55, 1 卷 54, 4
卷 54, 4 卷 54, 3
卷 54, 3 卷 54, 2
卷 54, 2 卷 54, 1
卷 54, 1 卷 53, 4
卷 53, 4 卷 53, 3
卷 53, 3 卷 53, 2
卷 53, 2 卷 53, 1
卷 53, 1 卷 52, 4
卷 52, 4 卷 52, 3
卷 52, 3 卷 52, 2
卷 52, 2 卷 52, 1
卷 52, 1 卷 51, 4
卷 51, 4 卷 51, 3
卷 51, 3 卷 51, 2
卷 51, 2 卷 51, 1
卷 51, 1 卷 50, 4
卷 50, 4 卷 50, 3
卷 50, 3 卷 50, 2
卷 50, 2 卷 50, 1
卷 50, 1 卷 49, 4
卷 49, 4 卷 49, 3
卷 49, 3 卷 49, 2
卷 49, 2 卷 49, 1
卷 49, 1 卷 48, 4
卷 48, 4 卷 48, 3
卷 48, 3 卷 48, 2
卷 48, 2 卷 48, 1
卷 48, 1 卷 47, 4
卷 47, 4 卷 47, 3
卷 47, 3 卷 47, 2
卷 47, 2 卷 47, 1
卷 47, 1 卷 46, 4
卷 46, 4 卷 46, 3
卷 46, 3 卷 46, 2
卷 46, 2 卷 46, 1
卷 46, 1 卷 45, 4
卷 45, 4 卷 45, 3
卷 45, 3 卷 45, 2
卷 45, 2 卷 45, 1
卷 45, 1 卷 44, 4
卷 44, 4 卷 44, 3
卷 44, 3 卷 44, 2
卷 44, 2 卷 44, 1
卷 44, 1 卷 43, 4
卷 43, 4 卷 43, 3
卷 43, 3 卷 43, 2
卷 43, 2 卷 43, 1
卷 43, 1 卷 42, 4
卷 42, 4 卷 42, 3
卷 42, 3 卷 42, 2
卷 42, 2 卷 42, 1
卷 42, 1 卷 41, 4
卷 41, 4 卷 41, 3
卷 41, 3 卷 41, 2
卷 41, 2 卷 41, 1
卷 41, 1 卷 40, 4
卷 40, 4 卷 40, 3
卷 40, 3 卷 40, 2
卷 40, 2 卷 40, 1
卷 40, 1 卷 39, 4
卷 39, 4 卷 39, 3
卷 39, 3 卷 39, 2
卷 39, 2 卷 39, 1
卷 39, 1 卷 38, 4
卷 38, 4 卷 38, 3
卷 38, 3 卷 38, 2
卷 38, 2 卷 38, 1
卷 38, 1 卷 37, 4
卷 37, 4 卷 37, 3
卷 37, 3 卷 37, 2
卷 37, 2 卷 37, 1
卷 37, 1 卷 36, 2
卷 36, 2 卷 36, 1
卷 36, 1 卷 35, 1
卷 35, 1 卷 34, 1
卷 34, 1 卷 33, 1
卷 33, 1 卷 32, 1
卷 32, 1 卷 31, 3
卷 31, 3 卷 31, 2
卷 31, 2 卷 31, 1
卷 31, 1 卷 30, 4
卷 30, 4 卷 30, 3
卷 30, 3 卷 30, 2
卷 30, 2 卷 30, 1
卷 30, 1 卷 29, 3
卷 29, 3 卷 29, 2
卷 29, 2 卷 29, 1
卷 29, 1 卷 28, 3
卷 28, 3 卷 28, 2
卷 28, 2 卷 28, 1
卷 28, 1 卷 27, 2
卷 27, 2 卷 27, 1
卷 27, 1 卷 26, 2
卷 26, 2 卷 26, 1
卷 26, 1 卷 25, 2
卷 25, 2 卷 25, 1
卷 25, 1 卷 24, 3
卷 24, 3 卷 24, 2
卷 24, 2 卷 24, 1
卷 24, 1 卷 23, 4
卷 23, 4 卷 23, 3
卷 23, 3 卷 23, 2
卷 23, 2 卷 23, 1
卷 23, 1 卷 22, 2
卷 22, 2 卷 22, 1
卷 22, 1 卷 21, 2
卷 21, 2 卷 21, 1
卷 21, 1 卷 20, 2
卷 20, 2 卷 20, 1
卷 20, 1 卷 19, 1
卷 19, 1 卷 18, 3
卷 18, 3 卷 18, 2
卷 18, 2 卷 18, 1
卷 18, 1 卷 17, 3
卷 17, 3 卷 17, 2
卷 17, 2 卷 17, 1
卷 17, 1 卷 16, 3
卷 16, 3 卷 16, 2
卷 16, 2 卷 16, 1
卷 16, 1 卷 15, 2
卷 15, 2 卷 15, 1
卷 15, 1 卷 14, 3
卷 14, 3 卷 14, 2
卷 14, 2 卷 14, 1
卷 14, 1 卷 13, 2
卷 13, 2 卷 13, 1
卷 13, 1 卷 12, 3
卷 12, 3 卷 12, 2
卷 12, 2 卷 12, 1
卷 12, 1 卷 11, 2
卷 11, 2 卷 11, 1
卷 11, 1 卷 10, 2
卷 10, 2 卷 10, 1
卷 10, 1 卷 9, 3
卷 9, 3 卷 9, 2
卷 9, 2 卷 9, 1
卷 9, 1 卷 8, 2
卷 8, 2 卷 8, 1
卷 8, 1 卷 7, 2
卷 7, 2 卷 7, 1
卷 7, 1 卷 6, 3
卷 6, 3 卷 6, 2
卷 6, 2 卷 6, 1
卷 6, 1 卷 5, 5
卷 5, 5 卷 5, 4
卷 5, 4 卷 5, 3
卷 5, 3 卷 5, 2
卷 5, 2 卷 5, 1
卷 5, 1 卷 4, 2
卷 4, 2 卷 4, 1
卷 4, 1 卷 3, 1
卷 3, 1 卷 2, 1
卷 2, 1 卷 1, 3
卷 1, 3 卷 1, 2
卷 1, 2 卷 1, 1
卷 1, 1
2025
1967