Low Phase Noise DAC-Based Frequency Synthesis for Fast Hopping Wideband Microwave Applications
Abstract
The excellent phase noise exhibited in ADI’s latest generation of high speed DACs enables size, weight, power/performance, and cost benefits in next-generation low phase noise, fast hopping agile RF/microwave synthesizers. A challenge is that to achieve this DAC capability, the fixed DAC sample clock must have very low SSB phase noise that is beyond the capability of mainstream wideband VCO PLLs. A method employing an analog phase detector (PD) is offered that can improve in-loop phase noise performance by 10 dB to 20 dB compared with conventional phase/frequency detector synthesizers. To meet the most demanding phase noise system requirements, the suggested fixed clock implementation is a dielectric resonator oscillator (DRO) locked using an analog PLL. Other more conventional examples are provided employing a commercially available MMIC VCO. The benefits of a DAC-based coarse/fine mixer microwave synthesizer are explained, with block diagrams, measured phase noise results, and an application circuit provided so that the interested engineer can try this in the lab.
Introduction
The aerospace & defense (ADEF) community has a justifiable obsession with phase noise. For example, radar, electronic warfare (EW), and a plethora of other applications require best-in-class phase noise performance from fast hopping frequency synthesizers and exciters. These frequency functional blocks often set critical system performance, such as radar clutter attenuation, and are used in larger frequency translation, tuner, and modulation schemes. ADI’s latest generation of high speed DACs exhibits extremely low additive phase noise that brings the long-standing dream of simplifying agile frequency generation architectures within reach. The evolution to DAC-based frequency synthesis enables much lower size, weight, power, and cost (SWaP-C) solutions replacing much larger, more expensive signal chains. In order to realize the phase noise potential, however, the system designer cannot use just any old sampling clock source scheme. This article explains the phase noise considerations and trade-offs when implementing a sample clock for best DAC phase noise. Taking things a step further, the article considers a low phase noise approach for implementing a wideband fast hopping synthesizer in the Ku-band to Ka-band range. An application circuit block diagram and measured data is provided so that the designer can duplicate the experimental data on her bench and leverage the approach in her design.
SSB Phase Noise Implications in EW and Radar
ADEF sensing systems need to intercept small signals or returns from enemy targets that do not want to be detected, in hostile electromagnetic environments, in a time-critical manner. Instantaneous spurious-free dynamic range (SFDR) is a figure of merit that is commonly used to express how well a receive system can sense small signals in the presence of large blockers. SFDR is expressed in terms of IMD2 or IMD3 and the noise floor, which is assumed to be uniform—that is, adequately offset from any carrier phase noise shoulders so as to avoid overcomplicating the equation with frequency offset dependence. This is an acceptable assumption outside of, say, 10 MHz from the carrier. However, EW and radar applications require operation closer to the carrier, inside this 10 MHz offset region. Therefore, an important aspect, which is not explicitly captured in SFDR, is how close to the transmitted carrier dynamic range can be maintained without getting buried in the noise shoulder of the carrier. This noise shoulder is the single sideband (SSB) phase noise and is expressed as a function of frequency offset from the carrier: ℒ(f).
Whereas communications and satcom systems might care more about a single integrated rms jitter number that integrates the total noise in the phase noise shoulder over an offset of interest, most radar and EW designers care more about the spot SSB phase noise envelope at specific frequency offsets from the carrier. Usually, this needs to be as low as possible, especially at Doppler offsets in the 1 kHz to 1 MHz range. The challenge for the synthesizer designer is that this critical mission region is often an elevated phase noise plateau associated with the phase-locked loop (PLL) noise construct. Minimizing the noise contribution in this zone is the main objective of this article.
If there is one takeaway from this article, remember that most radar and EW systems ideally want the sample clock SSB phase noise feeding the DAC ~10 dB below the DAC additive curve, allowing the DAC to set the phase noise floor of the system—not the clock! In practice, we will see this is very difficult. This is a testament to just how excellent Analog Devices’ DAC phase noise performance has become, and how transformative the potential is for DAC-based synthesizers.
Throughout this discussion, DPLL refers generally to any integrated PLL or synthesizer chip that employs an active phase/frequency detector (PFD) and frequency divider scheme. Figure 1 shows a classical digital PFD.


Figure 1. A classical digital phase/frequency detector (PFD).
APLL refers to employing a passive mixer as the phase detector (PD). To be clear, SSB phase noise suitability means something different to everyone based on specific mission requirements and application use case. Multi-octave microwave tuning, programmability, ease of use, and low SWaP-C are the modern advantages of wideband MMIC PLL-VCO synthesizers. For a broad majority of wideband tuned synthesizer applications not covered here, ADI’s integrated PLL-VCO synthesizers are the best choice. We are only considering this specific use case of a DAC fixed sample clock. For example, the descriptors used in Table 1 are meant to communicate the comparative performance as pertains to this niche use case.
What’s Different Now?
In the past, the barrier to implementing high speed DAC-based synthesis with a real IF was the DAC’s relatively low sampling rate (that is, 100 MSPS) and low analog frequency bandwidths (that is, 250 MHz). In using older DACs, the low IF makes up conversion difficult and forces some bulky, maybe impossible, RF filters. The other option, frequency multiplying, is impractical because the high required multiplication factor (referred to as N) translates to the DAC additive phase noise ℒDAC(f) to being too high, especially at the floor. A reminder of the impact of coherent frequency translation when upconverting from F1 to F2:

In other words, ADI’s lower sample rate DAC additive phase noise is good, but it rides on a direct carrier frequency that is too low to practically translate to microwave ranges at low SWaP-C.
Fast forward to today, and the game has changed. The DAC sampling rate, analog bandwidth, and resulting direct real IF frequency capability has increased to multi-GHz, the additive phase noise ℒDAC(f) remains excellent, and thus we finally have a versatile building block that opens up all sorts of new options for implementing low SWaP, microwave, wideband, fast tuning frequency synthesizers.
Wideband Microwave Synthesizers Using High Speed DACs
Figure 2 is a basic depiction of the DAC-based synthesizer we refer to herein. Each of the functional blocks contributes to overall phase noise a bit differently at different offsets from the carrier. The central point to this discussion is how to design each block so that the excellent DAC additive (also called residual) phase noise capability ℒDAC(f) sets the system phase noise. We are going to find out this isn’t trivial.
- ℒDAC(f) additive phase noise consists of multiple contributors, such as device 1/f noise and implementation techniques like shuffle mode. Power supply phase noise degradation is a notorious bogeyman, and careful low noise LDO implementation is critical.
- The reference oscillator FREF is the system phase reference signal to which the synthesizer will be locked, and is often in the 100 MHz range. ℒREF(f) is an absolute source phase noise that sets the synthesizer phase noise at the closest offsets, usually <1 kHz. Balancing the reference phase noise performance and frequency with SWaP-C is an important system trade-off: if the reference phase noise is not adequate, recovering phase noise downstream is somewhere between impossible and very painful. Don’t cut corners on the reference clock.
- The fixed frequency block is where the phase-locked loop (PLL) is located that locks a local RF voltage controlled source (RF source) to the frequency reference. Selection of the RF source absolute phase noise ℒRFsource(f) is another trade-off weighed against SWaP-C that sets the far offset phase noise where the shoulder meets the noise floor. The PLL technique is an additive phase noise contributor ℒPLL(f) that determines the phase noise at the critical mid-offset plateau (commonly 1 kHz to 1 MHz). The PLL active loop filter uses an op amp with a noise contribution that is important to consider and is lumped into this category. This mid-offset SSB phase noise region has the biggest impact to ℒRFDAC(f) and often makes or breaks synthesizer mission suitability. The first section of this discussion focuses on minimizing the sample clock phase noise ℒCLKDAC(f) to allow the DAC phase noise ℒDAC(f) to dominate ℒRFDAC(f).
- The tuned generator block is an additive phase noise contributor ℒgen(f) that mixes the DAC RF output with a set of fixed frequencies with absolute phase noise ℒcoarse(f) to upconvert to a wideband agile RF output. The second section of this discussion focuses on techniques to minimize phase noise ℒout(f) and spurs once you have your DAC output and need to translate it to higher microwave bands.


Figure 2. A block diagram of DAC-based wideband frequency synthesis and phase noise contributors.


Figure 3. Phase noise contributors to the overall DAC clock source phase noise.


Figure 4. The reason you need a lower phase noise sampling clock.
To summarize the important phase noise relations in Figure 2, Figure 3, and Figure 4:
The critical objective is for ℒDAC(f) to set ℒRFDAC(f), with as minimal contribution as possible from ℒCLKDAC(f).
ℒout(f < 1 kHz) is ℒREF(f < 1 kHz) + 20LogN (N = Final/reference frequency ratio).
ℒCLKDAC(f > 1 kHz) is highly dependent on how we choose to implement ℒRFsource(f) and ℒPLL(f). ℒREF(f) noise floor will play a role here too.
ℒout (f > 1 kHz) depends on above, plus how we choose to upconvert ℒRFDAC (f > 1 kHz). A method is recommended using ℒcoarse (f < 1 kHz).
New DAC Advantages, New Clocking Challenges
A colleague of mine cites conservation of grief as a natural law when traditional signal chains are re-vamped in favor of lower SWaP-C advancements. The law applies here as we need only a fraction of the old SWaP-C to do the DAC-based tuned generator functional block (grief decrease), but the fixed frequency source gets more nuanced (grief increase). Because the additive phase noise of the DAC is so low (a good thing—that is, the reason for this article), and because the sample clock is now pretty high at 12 GSPS (also a good thing that allows a real IF that can be reasonably filtered), the SSB phase noise required of the sample clock source forces us to consider more complex clock source solutions. In other words, using a MMIC VCO-PLL is not good enough to realize the DAC additive phase noise potential.
Let’s first consider the interplay of the reference oscillator, fixed frequency block, and DAC in Figure 2. The fixed frequency block consists of an RF voltage controlled oscillator (VCO) in a phase-locked loop that locks the RF source to the reference oscillator. The phase-locked loop consists of a frequency divider or translator, PFD, and active loop filter employing an op amp.
Three different implementation examples are compared in the discussion henceforth:
| Description | RF Osc | PD/PFD | SSB Phase Noise |
SWaP-C |
Ease of Use |
| MMIC VCO DPLL | MMIC VCO | Active PFD | Good | Best | Best |
| MMIC VCO APLL | MMIC VCO | Passive Mixer PD |
Better | Better | Poor |
| DRO APLL | DRO | Passive Mixer PD |
Best | Poor | Poor |
What’s Old Is New Again
Analog phase detectors are older than dirt and are the grandfathers of modern-day integrated active phase/frequency detector (PFD) synthesizers. They’ve been rendered obsolete in the vast majority of modern wideband synthesizer applications, and rightfully so given the advances in integrated synthesizer ICs. Analog PDs are a poor choice when a wideband tuned VCO-PLL is required at the best SWaP-C. So why choose an analog PD in this DAC clock use case? This has to do with the superior additive phase noise of the passive analog PD. The PD compares two input frequencies and outputs a beat signal that represents the phase difference. When the comparison frequencies are in quadrature, or locked, the PD outputs a 0 V DC signal. In integer-N and fractional-N synthesizers employing active PFDs, the maximum frequency at which the two compared input signals may operate is often around 100 MHz to 500 MHz. Synthesizer/PFDs like the HMC698 family can operate the PFD input as high as 1.3 GHz, which is beneficial to phase noise, at the expense of higher DC power. What’s most important is the active PFD contributes additive 1/f noise itself, and is highly dependent on the implementation—that is, not all are created equal. Hence the selection of the HMC440 in the example herein, which exhibits very low PFD 1/f noise. The rule of thumb to operate the PD at the highest frequency possible reduces the theoretical 20LogN increase of this in-loop additive PD phase noise plateau when translating the in-loop PD frequency to the RF output frequency. Translation loops like the ADF4401A exist to allow this highest possible PFD frequency while avoiding the noise from active frequency dividers.


Figure 5. Simplified block diagram of analog PLL (APLL).


Figure 6. Simplified block diagram of digital PLL (DPLL).
For example, let’s consider a phase-locked 10 GHz RF output signal using a PFD with additive noise of –153 dBc/Hz. To simplify things, we will assume the PFD is the dominant in-loop noise contributor (not always true). Running the PFD at 10 MHz will get in-band phase noise (that is, the plateau) of:

For the same exact scenario, let’s run the PFD frequency 10× higher at 100 MHz instead. The in-loop phase noise improves to:

The 20 dB benefit is enormous. Always clock your PFD as high as possible. There are a couple of advantages in using an analog mixer-based PD.
- The passive mixer additive noise is very low, such that it can often be ignored. The op amp active loop filter noise emerges as the in-loop limiting noise contributor.
- The comparison frequency can be as high as needed, often multiple GHz, which is balanced against the residual noise of in-loop components. Generally, the higher the frequency the smaller the available selection of adequately low residual noise RF amplifiers.
In summary, the optimal passive PD frequency is high enough so that the PD and in-band frequency divider additive noise is below the absolute phase noise of the multiplied up reference oscillator, but not too high such that RF amplifier residual noise degrades performance. Several RF amplifiers are required.
RF amplifier residual phase noise is a topic on its own. Process technology, as well as node and circuit architecture are big factors. Generally speaking, Si BJT offers the best performance, but is limited in frequency range (<1 GHz). GaAs HBT is the next best with parts generally available up through Ku-band (for example, ADL8150, HMC606LC5, HMC3653, and HMC3587).
pHEMT amplifiers are widely available at high frequencies but should be met with caution as residual phase noise varies widely. In general, pHEMT phase noise is not great and can exhibit temperature variation.
Figure 7 through Figure 10 illustrate the resulting DAC output signal phase noise ℒRFDAC(f) for the three clock implementation scenarios outlined in Table 1. Measured phase noise numbers are shown in Figure 18 through Figure 20. Figure 7 shows that a high performance DRO RF oscillator and analog phase-locked loop (DRO APLL) nudges against the DAC residual noise in a narrow region but can largely be considered “invisible” beneath the DAC noise. This offers much better performance than the traditional MMIC VCO DPLL sample clock in Figure 8, which dominates over a very wide offset range, wasting DAC phase noise capability, albeit offering the best SWaP-C and ease of use. The best balance of SWaP-C and performance might be the MMIC VCO APLL in Figure 9, which maintains DAC phase noise capability over a good stretch of critical offsets, but degrades performance toward the higher offsets due to the inferior MMIC VCO phase noise vs. the DRO. Figure 10 shows the composite overlay of the clock source options relative to the DAC additive phase noise.
It should be noted that even among DROs, SSB phase noise varies widely. The option used here is a small SWaP-C DRO about the size of a marble. Higher performance DROs exist, which could push the curve completely beneath the DAC residual noise. However, there is a direct correlation between DRO phase noise level and SWaP-C—that is, the solution will be much larger than a marble and could be thousands of dollars just for the DRO component!


Figure 7. DAC RF output SSB phase noise using DRO locked with analog PD.


Figure 8. DAC RF output SSB phase noise using MMIC VCO locked with active PFD.


Figure 9. DAC RF output SSB phase noise using MMIC VCO locked with analog PD.


Figure 10. DAC RF output SSB phase noise comparison of three approaches.
Microwave Synthesizer Implementation
Up to this point, we’ve considered the options in implementing the sample clock source relative to the DAC additive phase noise potential. Now we will consider the tuned generator implementation. The designer chooses a data converter sample clock frequency based upon a multitude of DAC and ADC objectives including Nyquist zone, instantaneous bandwidth, and data payload, among others. A fun puzzle is how to efficiently frequency plan the generation of a set of fixed tones from the available sample clock and the subharmonic, N-harmonic, and /N brethren thereof. These fixed tones are the coarse frequency set that are mixed with the fine frequency set output from the DAC.
Figure 11 is a block diagram of the coarse/fine mixing scheme. In this example, we are using the MxFE® RF ADCs AD9081/AD9082 with the sample clock at 12 GSPS from a VCO that also outputs RF/2 at 6 GHz. These tones come for “free” because you need them to clock the DAC, so it makes a lot of sense to base the coarse tone generator around them. It works out that 18 GHz feeding a programmable frequency divider to single sideband mixer scheme creates a set of coarse frequencies that, when mixed with the DAC output, allows synthesis coverage across most of Ku- and K-bands. Tunable band-pass filters are critical to attenuate many mixing and DAC spurs. A precision DAC translates the SPI control to a low noise analog control signal tuning the tunable filter (for example, ADV7125).


Figure 11. Recommended DAC-based coarse/fine mixer synthesizer using analog PD source.
Of course, this mixing scheme sounds a little complicated, and a brute force simpler option is to frequency multiply the DAC output instead of mix. Frequency multiplying is attractive because it is simpler and has lower SWaP-C, as the orange highlight functional blocks in Figure 11 are replaced with the multiplier functional block in Figure 12b. The problem with frequency multiplying, and why we don’t seriously consider it as an option here, is the 20LogN DAC noise floor and DAC spur degradation. The direct RF DAC output has excellent additive phase noise and spurious (generally miscellaneous spurs generated from DACs are well below 60 dBc). But to translate a 3 GHz to 6 GHz DAC RF output up to Ku-band, a multiply of 4 is needed at a minimum, which is a 12 dB degradation in DAC spurs and phase noise. From a mission standpoint, there’s a good chance this 12 dB degradation takes DAC spurs and noise from compliant to noncompliant.


Figure 12. (a) Lower performance alternative: integrated digital PLL sample clock. (b) Lower performance alternative: multiplier block.
The added complexity of the coarse/fine mixer approach is worth the trouble because it avoids multiplying the DAC, and thus the DAC spur and phase noise level are translated 1:1 to the upconverted RF output (not increased by 12 dB!)
Figure 13 through Figure 16 illustrate how the coarse and fine SSB phase noise combine to make the final SSB phase noise at the desired upconverted microwave frequency. Measured phase noise numbers are shown later in Figure 18 through Figure 20. Frequency multiplying is the same as mixing a signal with a copy of itself. Likewise, mixing coherent signals of different frequencies has the same 20LogN phase noise impact as multiplying. In other words, in Figure 13 through Figure 16, in the offset regions annotated “coherent,” there is no phase noise benefit from employing the mixing vs. multiplying approach. In upconverting the sample clock shown in gray to a higher LO frequency, the entirety of the phase noise curve is simply translated up 20LogN. The primary motivation for coarse/fine mixing is the benefit achieved at larger offsets as the phase noise shoulder approaches the noise floor. Because the LO coarse tone phase noise plunges far below the DAC additive noise level at these offsets, it contributes essentially nothing, and you just see the DAC phase noise translated 1:1 to the upconverted microwave signal. Figure 16 compares the final synthesizer phase noise for each approach and annotates the far offset benefit from mixing vs. multiplying.


Figure 13. Microwave synthesizer SSB phase noise using DRO locked with analog PD.


Figure 14. Microwave synthesizer SSB phase noise using MMIC VCO locked with active PFD.


Figure 15. Microwave synthesizer SSB phase noise using MMIC VCO locked with analog PD.


Figure 16. Microwave synthesizer SSB phase noise comparison of three approaches.
Figure 17 is the component chain used in the lab to get the measured SSB phase noise shown in Figure 18. An ultralow noise 100 MHz crystal oscillator is multiplied by 60. The resulting 6 GHz reference phase noise in Figure 18 has a floor of –137 dBc/Hz. As a sanity check this puts the 100 MHz crystal noise floor plus additive phase noise of the multiplication chain at –173 dBc, which makes sense. The reference 6 GHz signal feeds the LO port of the HMC558double balanced mixer, which is used as the analog PD. (Note that the IF port of the mixer must be DC coupled.) The PD constant (KPD) of the mixer is needed to calculate the op amp active filter values. This is measured experimentally using a mechanical delay line and voltmeter. The experimental setup measured both a DRO and MMIC VCO (HMC1166) at the RF oscillator spot. Because KVCO is a lot different between the two, different loop filter values are required. HMC606 is used so that the amplifiers do not add residual phase noise.


Figure 17. Evaluation circuit.

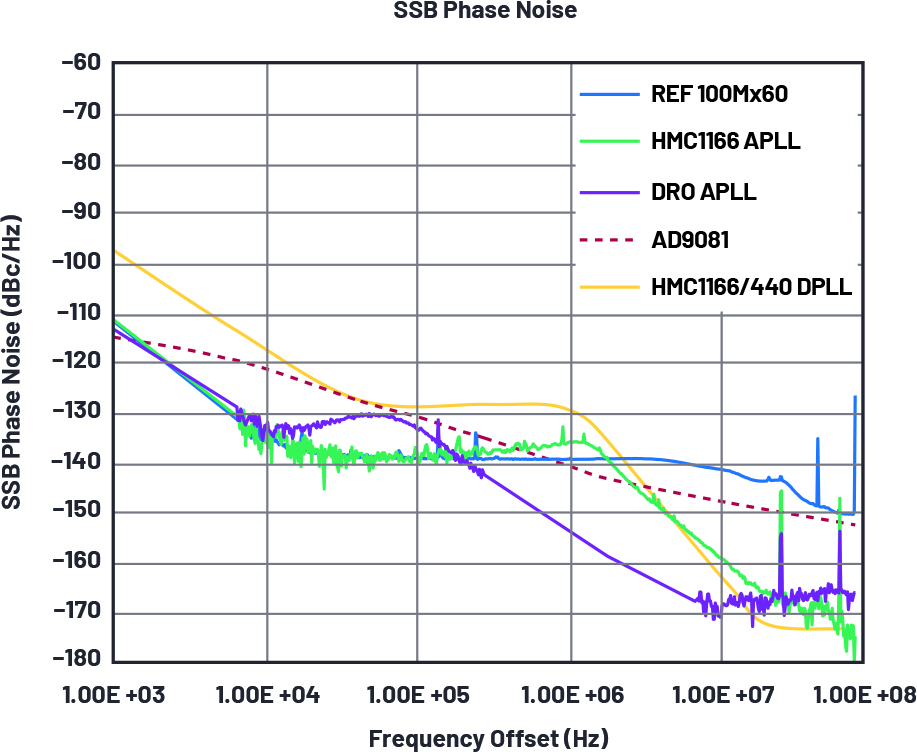
Figure 18. Measured SSB phase noise comparing sample clock scenarios, DAC additive, and reference. All traces normalized to the measured DAC output frequency 5.5 GHz.
As mentioned earlier, 6 GHz is chosen as the PD comparison frequency based upon the multiplied reference floor level at –137 dBc/Hz. The in-loop phase noise will be raised 20Log10 (12/6 GHz) = 6 dB, expressed as N=2. At this reference noise floor level, the op amp, frequency divider, and amplifier residual noise in the opposite leg are sufficiently below the reference floor so that they do not contribute. If 3 GHz PD frequency is chosen instead, the reference floor goes to –143 dBc/Hz (6 dB improved vs. 6 GHz scenario) and N=4 (6 dB worse vs. 6 GHz scenario), so the reference absolute phase noise impact to the final phase noise is a wash as the frequency scales up or down. However, the additive noise of the in-loop divider, amplifier, and op amp must now effectively be 6 dB better to remain non-contributors at 3 GHz. As the PD frequency lowers, you’ll reach a point where this additive noise dominates. Going the other way and increasing the PD frequency to 12 GHz removes the additive noise of the in-loop frequency divider (good) and might be viable. The additive noise of the RF amplifier will increase with frequency, but might be fine at 12 GHz. KPD would need to be remeasured at 12 GHz. The 12 GHz PD setup was not evaluated for this article, but this setup may work just fine.
If implemented in a product, a lock acquisition circuit is needed. This was not demonstrated. VTUNE needs to be “precharged” to steer the VCO frequency close enough to the reference so that lock can be captured.
In Figure 19, the measured phase noise results were impressive using the HMC1166 with analog PLL and AD829 op amp active loop filter. Using the same HMC1166 VCO, we demonstrated ~15 dB improvement using the analog PLL vs. the HMC440-based implementation using 1 GHz at the PD. Most importantly, the offset over which the clock dominates the phase noise is limited to 200 kHz to 2 MHz, and the worst-case degradation from the DAC additive phase noise is ~10 dB. Contrast this with the HMC440 implementation where the clock dominates an additional decade from 20 kHz to 2 MHz with a worst-case degradation of 17 dB from the DAC additive noise. At close offsets, the VCO APLL tracks the reference phase noise, with a bit of peaking from the loop filter at mid-offsets. This region around 500 kHz might be improved with further iteration. A suggested technique that showed promising results in modeling is to cut down the KVCO of the VCO. The above scenario uses readily available COTS components and is reasonably easy to demonstrate at low cost.


Figure 19. Measured DAC output SSB phase noise using VCO (HMC1166) locked using analog PLL. All traces normalized to the measured DAC output frequency 5.5 GHz.
The really exciting performance came from the DRO scenario in Figure 20, albeit at higher SWaP-C. Reflecting on the DRO APLL performance, we nearly got it low enough to be invisible under the DAC phase noise. The DAC RF output phase noise does bump up a few dB in the 10 kHz region where the CLK peaks close to the DAC phase noise. The loop bandwidth is quite narrow in order to get the optimal transition point to the very low DRO phase noise. The peaking of the DRO APLL is suspected to be op amp noise. Overall, we feel the objective was met within a couple dB and can recommend a 12 GHz DRO locked using an analog PLL for the lowest phase noise synthesizers needing the full phase noise capability from MxFE devices.


Figure 20. Measured DAC output SSB phase noise using DRO locked using analog PLL. All traces normalized to the measured DAC output frequency 5.5 GHz.Other Benefits.
Other Benefits Using a DAC-Based Mixer Synthesizer
In addition to phase noise benefits, the MxFE DAC-based coarse/fine mixer synthesizer is capable of ~300 ns agile frequency hopping when in fast frequency hop (FFH) NCO-only mode. When hopping among the 32 independent NCOs, frequency hop phase coherency is maintained, as shown in Figure 21. Additionally, this synthesizer is not limited to just agile tone generation. The DAC provides the flexibility to implement arbitrary modulation implemented via the JESD204B/ JESD204C datalink.


Figure 21. Frequency hop phase coherency.
Conclusion
The excellent phase noise exhibited in ADI’s latest generation of high speed DACs (AD9162, AD9164, AD9172, AD9174, AD9081, AD9082, for example) enables SWaP-C benefits in next-generation low phase noise, fast hopping, agile RF/microwave synthesizers. The fixed DAC sample clock must have very low SSB phase noise that is beyond the capability of mainstream wideband VCO-PLLs. Analog PDs can offer 10 dB to 20 dB of in-loop phase noise performance improvement vs. conventional active PFD-based PLL synthesizers. To meet the most demanding phase noise system requirements, the suggested fixed clock implementation is a DRO locked using an analog PLL. DAC-based coarse/fine mixer synthesizer examples, measured phase noise results, and an application circuit are provided.
Related to this Article
Products
RECOMMENDED FOR NEW DESIGNS
MxFE™ Quad, 16-Bit, 12GSPS RFDAC and Quad, 12-Bit, 4GSPS RFADC
RECOMMENDED FOR NEW DESIGNS
16-Bit, 12 GSPS, RF DAC and Direct Digital Synthesizer
RECOMMENDED FOR NEW DESIGNS
Translation Loop, PLL, VCO Module
Apollo MxFE Quad, 16-Bit, 28GSPS RF DAC and Quad, 12-Bit, 20 GSPS RF ADC
11.41 GHz to 12.62 GHz MMIC VCO with Half Frequency Output
7 GHz Integer-N Synthesizer SMT
SMT 2.8 GHz Integer-N Synthesizer (N = 2 - 32)




















