AN-924:数字正交调制器增益
简介
数字正交调制器出现在众多通信及信号处理IC中。本应用笔记旨在说明数字正交调制器的基本构建模块,并分析三类输入信号在调制器中产生的增益。
普通数字调制器由一对数字乘法器和一个数字加法器构成,如图1所示。一般地,与数据路径相关的二进制数字都有着相同的数字范围,即±1。这种情况适用于输入(I、Q和载波)、输出(Y)以及中间数字路径。出于一般性考虑,图中所示总线宽度为N位,代表−1和+1之间的小数值。

图1. 数字正交调制器功能框图
在四个输入端中,有两个专门用于处理数字载波信号,这是构成正交载波的正弦波和余弦波的N位量化表示。根据定义,载波拥有独立的正弦和余弦分量,二者均以载波角频率ωC振荡(数字式)(其中,ωC等于2πfC,fC表示单位时间周期数)。另外两个输人端(1和Q)用于处理一个N位量化数字基带信号。I和Q这两个分别是基带信号中的同相(in-phase)和正交(quadrature)相位分量的缩写。输出端Y是上变频至载波频率(fC)的基带信号的N位量化数字表示。
输入信号与输出信号之间的关系可以表示为一个时间函数,如等式1所示。
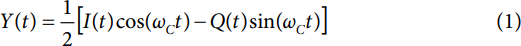
V½是在加法器的输入端和输出端使用相同位数的结果。其原因在于,两个N位乘法器输出之和实际要求N+1位表示全部结果之和。然而,将加法器输出限制为N位意味着,必须放弃N+1位结果中的最低有效位。截断成N位必然会使加法器位数丢失50%,这就是等式1中比例因子确立为%的原因所在。
接下来分析三类不同I及Q输入信号下的输出信号Y(t)。涉及的输入信号类型为
- 静态输入信号
- 非正交正弦输入信号
- 正交正弦输入信号
以下分析使用了等式2和等式3确立的三角恒等式。另外,等式4中的公式可用于正交信号分析。该等式将正交表达式(左侧)与余弦函数(右侧)相关联。尤其需要注意的是,当将等式4代人等式1时,结果会得到Y(t)的等价形式,如等式5所示。
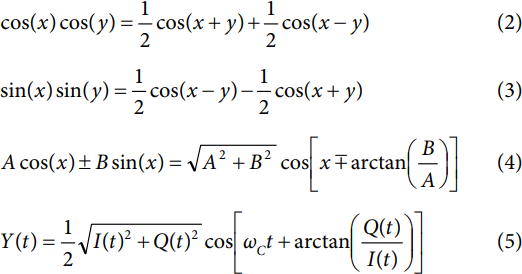
静态输入信号分析:I(t) = D且Q(t) = E
这种情况下,输入信号I和Q与时间无关,而分别是D和E产生的静态值。D和E被设为0与1之间的小数值(含0和1),即二者代表最大可能峰值输入值的小数部分。据等式5,Y(t)可表示为
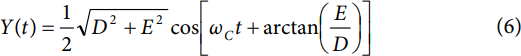
注意,等式6中余弦函数的自变量只含有一个频率分量(ωC)。即是说,输出信号是具有与载波信号相同频率的单音。但输出信号的相位随弧度角arctan(E/D)而增加,对应着正交载波输入信号中余弦分量的相位。另外,输出信号的幅度取决于D和E的矢量和。在D等于E的特殊情况下(即D = E = k (0 ≤ k ≤ 1)),Y(t)可简化为

可考虑k = 1的特殊情况,即I和Q输人为静态满量程值。当k = 1时,Y(t)的峰值为√2/2,表示在最大可能峰值输出值为1时,增益为−3 dB。归一化输出功率为√2/2)2 = ½,或者说在最大可能输出功率(1)2 = 1时,增益为-3dB。
非正交正弦输入信号分析:I(t) = A × cos(ωBt)且Q(t) = B × cos(ωBt)
这种情况下,输入信号I和Q为正弦信号。两个正弦信号都具有任意基带角频率ωB,无相对相位偏移(即两个信号为同相)。另外,信号I由常数A (0 ≤ A ≤ 1)进行缩放,信号Q则由常数B (0 ≤ B ≤ 1)缩放。据等式5,输出信号可表示为
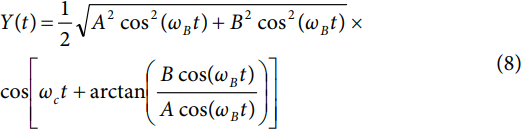
简化为
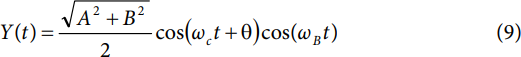
注意,与静态输入信号类似,载波表现出恒定相移,公式为θ = arctan(B/A)。
将等式2代入等式9中的Y(t),则有
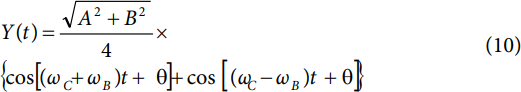
注意Y(t)由两个余弦函数构成。其中之一包含角频率项ωC + ωB,另一个包含角频率项ωC − ωB;但两者都表现出θ = arctan(B/A)的相移。可见,Y(t)由两个信号音构成,二者均为基带频率(fC)偏移载波频率(fB)。此外,各信号音的振幅缩放量为

可考虑A= B= 1的情况,即信号I和Q的峰值为满量程输入范围的极值。此时,各输出信号音的峰值变为√2/4,相位偏移(θ)则为π/4弧度。各输出信号音的峰值为√2/4意味着当最大可能峰值输出值为1时,增益为−9 dB。但是,两个信号音处于不同的频率,意即其复合振幅的峰值相当于任一信号音的两倍(与0值无关)。因此,Y(t)的峰值振幅为2(√2/4) = √2/2, 表示在最大可能峰值输出值为1时,增益为−3 dB。
每个信号音的归一化功率为(√2/4)2 = ⅛。由于总功率等于各信号音功率之和,因此总功率为¼。结果,相对于最大可能输出功率(1)2 = 1 (峰值为1的单个正弦波的功),Y(t)的功率损失为6 dB。
注意,如果用正弦函数代替输入信号,结果与此处的结果相同,唯一区别是Y(t)含有正弦函数。
非正交正弦输入信号分析:I(t) = A × cos(ωBt)且Q(t) = B × sin(ωBt)
这种情况下,输入信号I和Q构成-一个正交信号音(分别为余弦函数和正弦函数),其基带角频率为ωB。信号I由A (0 ≤ A ≤ 1)行缩放,信号Q则由B (0 ≤ B ≤ 1)缩放。据等式1,Y(t)可表示为
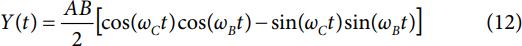
将等式2和等式3代入等式12中的Y(t),该等式可简化为

注意,Y(t)仅含有一个余弦项,即是说Y(t)由单个信号音构成。其角频率为基带角频率ωB)与载波角频率(ωC)之和,且信号音的振幅由½AB比例放大。
可考虑A= B= 1的情况,即信号I和Q的峰值均为满量程输入范围的极值。此时,Y(t)为

注意,单个信号音输出的峰值振幅为½,表示在最大可能峰值输出值为1时,增益为−6 dB。归一化输出功率为(½)2 = ¼,表示在最大可能输出功率(1)2 = 1的时候,功率损失为6 dB。
固有衰减
以上各节显示,N位数字正交调制器表现出一种固有衰减,取决于I、Q两个输入端的信号类型。三类输入信号的衰减因子如下所示:
- 静态:−3 dB
- 非正交信号音:−3 dB复合(各信号音−9 dB)
- 正交信号音:−6 dB
对于数字正交调制器的固有衰减,可以通过在调制器输出端添加一个数字乘法器来加以克服。该乘法器充当一个放大器,用于补偿调制器的固有衰减。在不发生数字溢出的情况下允许的放大量取决于I、Q两个输入信号的振幅。然而,对于满量程I、Q输入信号,必须对放大因子进行上限限制,以避免数字溢出。当输入信号为正交信号音时,放大因子必须限制为2.0(或6dB)。当输入信号为非正交信号音或静态值时,放大因子必须限制为1.414(或3dB)。
固有功率损失
N位数字正交调制器的固有衰减会导致与满量程N位正弦信号音相关的信号功率损失。功率损失程度取决于施加于I、Q两个输入端的信号类型。三类输入信号的相对输出功率如下所示:
- 静态:−3 dB
- 非正交信号音:−6 dB复合(各信号音−9 dB)
- 正交信号音:−6 dB
当调制器驱动DAC且频谱分析仪连接至DAC输出端以测量信号功率时,与不同输入信号相关的功率损失较为明显(见图2)。由于调制器有一个N位输出端,因此其基准功率为N位量化正弦信号音的基准功率。此类信号音用频谱分析仪测得的功率水平用作以下讨论的基准水平,表示为0dBr。

图2. 相对功率谱
当用N位数字调制器驱动N位DAC(如图1所示)时,输出功率取决于I、Q输入端的信号类型。具体地说,当调制器的I、Q两个输入端由满量程静态输入信号驱动时,DAC输出单音,载波频率为(fC),输出功率水平为−3 dBr。当调制器的I、Q两个输入端由满量程正交信号音驱动时,DAC输出单音,频率为fC+ fB,输出功率水平为−6 dBr。 当调制器的I、Q两个输入端由满量程非正交信号音驱动时,DAC输出信号由两个频率(fC ± fB)构成,各信号音的输出功率水平均为−9 dBr。复合信号功率(两个信号音复合)为 −6 dBr,为任一输出信号音功率的两倍。
