Oscillator Design Considerations for Low-Current Applications
Abstract
This application note describes how low-frequency oscillator design and crystal selection affect operating current. When running the oscillator from a limited-capacity supply, such as a lithium coin cell or super capacitor, minimizing the operating current increases the operating time.
Introduction
Maxim has a large portfolio of low-power, battery-backed real-time clocks (RTCs). A primary consideration when Maxim designs an RTC is minimizing the power requirements of the oscillator when the RTC is running from the backup supply, so as to maximize the life of the backup source. Crystal oscillators provide reasonable accuracy, and development efforts for many years have focused on minimizing power consumption.
Oscillator design goals include the following:
- Provide enough current and gain to start and maintain oscillation
- Provide a wide operating-voltage range
- Minimize the influence of external noise on accuracy
Key Crystal and Oscillator Parameters
Figure 1 presents an equivalent circuit of a crystal resonator. A crystal has two frequencies of zero phase, as shown in Figure 2. The lower frequency is the series resonant frequency. At the series resonant frequency, L1 and C1 cancel, and the impedance is determined by R1.1 The second, higher, frequency is the parallel resonant frequency. At parallel resonance, resistance is at a maximum.
A parallel resonant oscillator circuit (Figure 3) uses a crystal that is designed to operate with a specified load capacitance. This results in a circuit that operates at a frequency between the series resonant point and the parallel resonant point. A change in the load capacitance causes a change in the oscillator frequency.
Crystal equivalent series resistance (ESR) tends to shift upwards after going through SMT reflow, so an SMT crystal that is otherwise similar to a through-hole package crystal may have a higher maximum ESR specification. Likewise, smaller tuning-fork crystals will usually have higher ESR specifications than larger ones.

Figure 1. Equivalent circuit of a crystal resonator.

Figure 2. Crystal phase and impedance response.

Figure 3. Pierce-type (inverter variation) oscillator circuit.
Oscillator Current
As Eric Vittoz has observed, when both load capacitors in a crystal oscillator circuit (Figure 3) are of equal value, the minimum current for oscillation (or critical transconductance) can be approximated by the equation below.2
gmcrit ≈ 4ω2 × CL2 × RESR
Where ω is the frequency in radians, CL is the equivalent capacitive load, and RESR is the ESR of the crystal. The oscillator is assumed to be a CMOS device operating in weak inversion.
Vittoz also determines that the oscillator amplitude and bias current are related by the following equation:
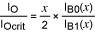
Where  and IB0 and IB1 are zero- and first-order modified Bessel functions.
and IB0 and IB1 are zero- and first-order modified Bessel functions.
We can therefore show the relationship between oscillator current at a given oscillator voltage with different values of ESR and CL, as shown in the following example. Assuming that V1 = 400mVP-P, nUT = 26mV, ESR = 35kΩ, and CL = 6pF, then  ≈ 4, and
≈ 4, and
IO ≈ 4ω2 × CL2 × RESR × nUT × 4
≈ 4 × (32,768 × 6.283)2 × (6e-12)2 × 35e+3 × 0.026 × 4
≈ 22.2nA.
Table 1 shows the relationship between both CL and ESR on oscillator current, using the values for V1 and nUT above.
| ESR (Ω) | CL (pF) | IO (nA) |
| 35,000 | 6 | 22.2 |
| 70,000 | 6 | 44.4 |
| 35,000 | 12.5 | 88.9 |
| 70,000 | 12.5 | 177.8 |
Since in the equation for gmcrit the CL term is squared, doubling the load capacitance has the effect of increasing oscillator current by four times. Increasing the crystal ESR by two times causes the required oscillator current to double. Note that this is the minimum estimated oscillator current, which does not include current consumed by additional circuits for amplifying the oscillator output, nor does it include currents in the devices used to divide the frequency down to 1Hz.
Oscillator Design Requirements
An oscillator should be designed so that it has sufficient gain to operate over the entire operating temperature and voltage range. The amplitude must always be sufficient to drive the following gain and buffer stages under operating conditions. To minimize oscillator current requirements, for a given oscillation voltage, a low CL is desired. Lower CL, however, will increase an oscillator's susceptibility to the influence of external noise. Poor availability of low CL crystals may make selection of a crystal with a higher CL necessary, at the cost of increased oscillator current. Likewise, if a design requires a small crystal package, an oscillator design that will drive a high ESR crystal is needed, increasing the necessary oscillator current.
Additionally, circuits used to add desirable functions, such as glitch filters to improve oscillator noise immunity, or circuits to detect when the oscillator has stopped, will add to the circuit's overall current consumption.3
Conclusion
There are a number of tradeoffs to be considered when designing an oscillator for a low-power RTC. Increasing CL will increase noise immunity and may provide a larger selection of crystal models to choose from, at the expense of oscillator current. Likewise, designing an oscillator so that it will run with relatively high ESR crystals requires higher oscillator currents. Adding a glitch filter or oscillator stop detection circuit also adds beneficial functions, but draws additional current.
References
1 Ecliptek Corporation, "Glossary of Terms for Crystals," www.ecliptek.com.
2 Eric A. Vittoz, "High-Performance Crystal Oscillator Circuits: Theory and Application," IEEE Journal of Solid-State Circuits, Vol. 23, No. 3 (June 1988).
3 See the Oscillator Stop Flag (OSF) bit description in the DS1337, DS1338, DS1339, DS1340, DS1341, DS1388, DS1390/91/92/93, and DS1318 data sheets.