AN-1026:高速差分ADC驱动器涉及考虑
简介
多数现代高性能ADC都利用差分输入来抑制共模噪声及干扰,将动态范围提高2倍,并通过平衡信号提高总体性能。尽管带差分输入的ADC可以接受单端输入信号,但在输入差分信号时,ADC的性能才能达到最佳状态。ADC驱动器一通常设计用于提供此类信号的电路一执行多种重要功能,包括幅度缩放、单端-差分转换、缓冲、共模失调调整、滤波等。自AD8138推出以来,差分ADC驱动器已成为数据采集系统中必不可少的信号调理元件。
ADC驱动器多一个输出引脚(VON) 和输入引脚(VOCM)。将信号接入带差分输入端的ADC时,这些引脚可带来极大的灵活性。

图1. 差分放大器
图1所示为一种基本的全差分电压反馈ADC驱动器。可见,其与传统的运算放大器反馈电路存在两点差异。差分ADC驱动器多一个输出引脚VON和输入引脚 VOCM。将信号接入带差分输入端的ADC时,这些引脚可带来极大的灵活性。
差分ADC驱动器产生的不是单端输出信号,而是在 VOP 和 VON 之间以 VOCM 为参考产生平衡差分输出信号。(P表示正极,N表示负极。)输入端 VOCM 用于控制输出共模电压。只要输入与输出处于各自限度之内,输出共模电压一定等于应用于VOCM 输入端的电压。负反馈和高开环增益公便 VA+ 和 VA–两个放大器输入引脚处的电压实际上相等。
出于下文讨论需要,在此先明确一些定义。如果綸人平衡信号, VIP 和 VIN 以共同基准电压为参照,其名义幅度相等、相位相反。当输入单端信号时,一个输入端电压固定,另一输入端则因其而变化。两种情况下,输入信号均定义为 VIP − VIN。
差模输入电压VIN, dm 以及共模输入电压VIN, cm分別由等式】和等式2定义。


对于平衡输入信号,该共模定义一目了然,但对单端输入信号同样有效。
输出电压同样有差模和共模两种,分别由等式3和等式4定义。


请注意实际输出共模电压(VOUT, cm)与 VOCM 输入引脚之差,后者用于确定输出共模电平。
分析差分ADC驱动器比分析传统运算放大器要复杂得多。为了简化代数式,不妨定义两个反馈因子 β1 和 β2如等式5和等式6所示。


在多数ADC驱动应用中,β1 = β2,但以 VIP, VIN, VOCM, β1和 β2为因子, VOUT, dm的般闭环等式可用于了解阝失配是如何影响性能的。等式7所示 VOUT, dm等式包括放大器有限频率依赖性,开环电压增益A(s)。

当 β1 ≠ β2时,差分输出电压取决于VOCM,这种结果并不理想,因为它会在差分输出中产生失调和过量噪声。电压反馈结构的增益带宽积为常数。有趣的是,增益带宽积中的增益为两个反馈因子平均值的倒数。
当 β1 = β2 ≡ β时,等式7可简化为8。

这个等式更为眼熟;当A(S)>∞时,理想闭环增益简化为 RF/RG 。增益带宽积同样眼熟,噪声增益等于1/β, 与传统运算放大器一样。
匹配反馈因子差分ADC驱动器的理想闭环增益如等式9所示。

作为差分ADC驱动器的重要性能指标之一的输出平衡包括两个部分:幅度平衡和相位平衡。幅度平衡是衡量两个输出在幅度上的匹配程度的一项指标;在理想放大器中,二者精确匹配。输出相位平衡这项指标旨在衡量两个输出的相位差离180°的距离。输出幅度或输出相位若存在失衡,结果会在输出中产生不良共模成分。输出平衡误差(等式10)为差分输入信号产生的输出共模电压与同一输入信号产生的输出差模电压之对数比,单位为分贝。

内部共模反馈环路迫使 VOUT, cm 等于应用于VOCM 输入的电压,结果产生良好的输出平衡。
将输入引脚端接至ADC驱动器
ADC驱动器通常用在处理高速信号的系统中。距离超过信号波长一小部分的器件必须通过阻抗受控的电气传输线相连,以防止损失信号完整性。当传输线两端均以其特性阻抗端接时,可获得最佳性能。驱动器一般置于ADC附近,因此两者中间不需要受控阻抗连接;然而,鉴于至ADC驱动器输入端的输入信号连接较长,必须使用一个受控阻抗连接,并按适当电阻进行端接。
ADC驱动器的输入电阻,无论属于差分还是单端性质,都必须大于或等于日标端电阻,以便添加一个端电阻 RT,与放大器输入端并联,以获得所需电阻。在此处考虑的各示例中,所有ADC驱动器均采用平衡反馈比设计,如图2所示。

图2.差分放大器输入阻抗
由于负反馈使放大器两个输入端之间的电压变成零,因此,两个输入端为虚联接,差分输入电阻 RIN仅为 2 × RG为了匹配传输线电阻 RL,将电阻 RT 通过等式11计算得出)置于差分输入上。图3所示为典型电阻 RF = RG = 200 Ω, 目标 RL, dm = 100 Ω 且 RT = 133 Ω。

图3.匹配 100 Ω 线路

端接单端输入要麻烦许多。图4展示了ADC驱动器在单端输入及差分输出下的工作方式。

图4.至ADC驱动器的单端输人示例
虽然输入为单端性质,但 VIN, dm 仍等于 VIN。由于电阻 RF 和 RG 相等且平衡,故为单位增益,且差分输出 VOP − VON等于输入,即 4 V p-p。 VOUT, cm 等于 VOCM = 2.5 V 来自低反馈电路的两个输入电压 VA+ 和 VA− 等于 VOP/2。
利用等式3和等式4,可得 VOP = VOCM + VIN/2, ±1 V 同相摆动约 2.5 V。 VON = VOCM − VIN/2, ±1 V 反相摆动约 2.5 V。因此, VA+ 和 VA− 在±0.5 V下约摆动1.25 V。必须由 VIN 提供的电流的交流成分为 (2 V – 0.5 V)/500 Ω = 3 mA, 因此,必须匹配的接地电阻(从 VIN看过去)为 667 Ω.
在各环路反馈因子相匹配时,确定单端输入电阻的通用公式为等式12,其中, RIN, se 单端输入电阻。

这是计算端电阻的第一步。然而,需要注意的是,各放大器增益等式均基于阻抗输入源为零的假设。当存在由单端输入导致的失衡时,必须相匹配的有效源阻抗只会给上位电阻 RG增加电阻。力保持平衡,必须给低位电阻 RG,增加电阻,但这又会影响增益。
虽然在端接单端信号时可采用闭式解,但迭代法更为常用。在以下示例中,选代法的作用更加明显。
图5中,为保持低噪度,需要一个值力1的单端转差分增益,一的输入引脚以及值接近 200 Ω 的若千反馈电阻和增益电阻。

图5.单端输入阻抗
利用等式12可算出单端输入电阻 2。根据等式13可知,要使267 Ω 的输入电阻降至50 Ω,并联电阻RT 应为 61.5 Ω。

图6所示电路给出了源电阻和端电阻。当源电阻值为 时,源电阻的开路电压为2VP-P。当源电阻端接于50 Ω时,输入电压降为1VP-P,该值同时为单位增益驱动器的差分输出电压。

图6.带源电阻和端电阻的单端电路
该电路给人的第一印象是完整,但仅上位电阻 RG就添加了一个61 Ω的未匹配电阻,与50 Ω电阻并联。这会改变增益及单端输入电阻,并使反馈因子失去匹配。对于小增益,输入电阻的变化较小,可暂时忽略不计,但反馈因子仍然必须得到匹配。最简单的方法是给低位电阻 RG增加电阻。
图7所示为一种戴维宁等效电路,其中,前述并联组合充当源电阻。
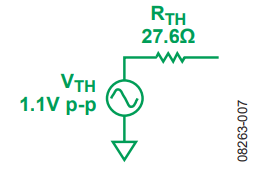
图7.戴维宁等效输入源
在该替代电路中,向低位环路增加了一个 27电阻 RTS,以便匹配环路反馈因子,如图8所示。

图8. 平衡单端端极电路
注意,1.1Vp-p的戴维宁电压大于1Vp-p的正确端接电压,各个增益电阻的值均增加27.6 Ω,结果降低了闭环增益。在大电阻(>1k2)和小增益(1或2)的情况下,这种反向作用可相互抵消,但在小电阻或高增益情况下,并不能完全抵消。
现在,我们可以轻松地分析图8所示电路,其差分输出电圧可利用等式14計算。

差分输出电压并未完全处于1Vp-p的理想水平,但可通过修改反馈电阻来独立对增益进行最终调整,如等式15所示。

图9展示的是完整电路,采用标准1%电阻值。

图9.完整单端端极电路
参照图9,因 RF 和 RG 两个电阻发生变化,驱动器的单端输入电阻 RIN, se也随之变化。驱动器的增益电阻在上位环路中为 ,下位环路中为200 Ω + 28 Ω = 228 Ω 。在不同的增益电阻值下,计算 RIN, se首先需要计算两个B值,分别如等式16和等式17所示


输入电阻 RIN, se的计算方法如等式18所示。其结果与最初算出的267 Ω 差别不大,对RT,不会产生大的影响,因为 RIN, se 与 RT属于并联关系。

如果需要更加精确的总增益,可使用更高精度的电阻和串联调整电阻。
当闭环增益为1或2时,此处所述方法选代一次即可。对于更高增益, RTS 的值接近 RG,根据等式18算出的 RIN, se。值与根据等式12求得的值之差将变大。这类情况需要进行多次达代。
这个任务不算艰巨:最近发布的差分放大器计算器工具 ADIsimDiffAmp"及ADI Diff Amp Calculator"可以承担所有 繁重劳动,仅需数秒即可完成以上计算。有关更多信息, 请参看 www.analog.com。
输入共模电压范围(ICMVR)
ICMVR规定可应用于差分放大器输入端而不影响正常运行的电压范围。这些输入端出现的电压可称为 VACM或 VA±。但这一规格经常被误解。最常见的困难是确定差分放大器输入端的实际电压,尤其是相对于输入电压而言VIN, cm, β和 VOCM 三个变量的情况下,可算出放大器输入电压 (VA±) ,各B不等时使用通用等式19,各B相等时使用简化等式20。


注意, VA始终是输入信号的缩小版本(如图4所示)。输入共模电压范围因放大器的类别而异。ADI高速差分ADC驱动器有两种输入级配置,分别为中心型和偏移型。中心型 ADC驱动器的每个供电轨都有约1V的裕量(因而称为中心型)。偏移型输入级增加了两个晶体管,以允许输入端尽量靠近–VS 轨摆动。图10所示为一种典型的差分放大器的简化输入示意图(Q2和Q3)。

图10. 简化版差分放大器(偏移型ICMIVR)
偏移型输入结构允许差分放大器处理双极性输入信号,即使放大器由单电源驱动也是如此,特别适合采用地电压或地电压以下输入的单电源应用。输入端增加的PNP品体管(Q1和Q4)将输入向差分对偏移一个品体管 VBE。例如,若 -IN应用电压为-0.3V,则A点为0.7V,使差分对可以正常运行。若无PNP(中心型输入级),A点-0.3V的电压会使NPN差分对发生反向偏置,并中断正常运行。
表1为ADI ADC驱动器的多种规格参数提供了快速参考,包括哪些驱动器采用了偏移型ICMVR配置,哪些未采用。
| ADC驱动器 | 电源电压(V) | 偏离供电轨的 输出摆幅 (V) |
ISUPPLY(mA) | ||||||||||
| ICMVR | VOCM | ||||||||||||
| 产品型号 |
带宽 (MH) |
压摆率 (V/µs) |
噪声 (nV) | ±5 V1 | +5 V | +3.3 V1 | +3 V1 | ±5 V | +5 V | +3.3 V1 | +3 V1 | ||
| AD8132 | 350 | 1200 | 8 | −4.7 至 +3 | 0.3 至 3 | 0.3 至 1.3 | 0.3 至 1 | ±3.6 | 1 至 3.7 | N/A | 0.3 至 1 | ±1 | 12 |
| AD8137 | 76 | 450 | 8.25 | −4 至 +4 | 1 至 4 | 1 至2.3 | 1 至2 | ±4 | 1 至 4 | 1 to 2.3 | 1 至 2 | 轨到轨 | 3.2 |
| AD8138 | 320 | 1150 | 5 | −4.7 至+3.4 | 0.3 至 3.2 | N/A | N/A | ±3.8 | 1 至 3.8 | N/A | N/A | ±1.4 | 20 |
| AD8139 | 410 | 800 | 2.25 | −4 至 +4 | 1 至 4 | N/A | N/A | ±3.8 | 1 至 3.8 | N/A | N/A | 轨到轨 | 25 |
| ADA4927-1/ADA4927-2 | 2300 | 5000 | 1.4 | −3.5 至 +3.5 | 1.3 至 3.7 | N/A | N/A | ±3.5 | 1.5 至 3.5 | N/A | N/A | ±1.2 | 20 |
| ADA4932-1/ADA4932-2 | 1000 | 2800 | 3.6 | −4.8 至 +3.2 | 0.2 至 3.2 | N/A | N/A | ±3.8 | 1.2 至 3.2 | N/A | N/A | ±1 | 9 |
| ADA4937-1/ADA4937-2 | 1900 | 6000 | 2.2 | N/A | 0.3 至 3 | 0.3 至 1.2 | N/A | N/A | 1.2 至3.8 | 1.2 至 2.1 | N/A | ±0.9 | 40 |
| ADA4938-1/ADA4938-2 | 1000 | 4700 | 2.6 | −4.7 至 +3.4 | 0.3 至 3.4 | N/A | N/A | ±3.7 | 1.3 至 3.7 | N/A | N/A | ±1.2 | 37 |
| ADA4939-1/ADA4939-2 | 1400 | 6800 | 2.3 | N/A | 1.1 至 3.9 | 0.9 至 2.4 | N/A | N/A | 1.3 至 3.5 | 1.3 至 1.9 | N/A | ±0.8 | 37 |
| 1 N/A = 不适用 | |||||||||||||
输入和输出耦合:交流或直流
需要交流耦合还是直流耦合可能对差分ADC驱动器的选择起着重要的影响。输入耦合和输出耦合两种情况有不同的考虑。
交流耦合输入级如图11所示。

图11.交流耦合ADC驱动器
对于带交流耦合输入端的差分转差分应用,出现在放大器输入引脚处的直流共模电压等于直流输出共模电压,因为输入电容阻断了直流反馈电流。同时,直流下的反馈因子相互匹配且完全与单位值相等。 VOCM及直流输入共模电压通常设置在电源电压一半附近。采用中心型输入共模范围的ADC驱动器在这类应用中工作良好,其输入共模电压接近标定范围的中心。
当输入耦合可选时,值得注意的是,带交流耦合输入的ADC驱动器的功耗低于带直流耦合输入的类似驱动器,因为两个反馈环路中都不存在直流共模电流。
交流耦合,当ADC要求输入共模电压与驱动器输出端的可用电压相差很大时,可对ADC驱动器的输出端进行交流耦合。当 VOCM 设为电源电压一半附近时,驱动器的输出摆幅最大;在驱动要求极低输入共模电压的低电压ADC时,这会带来一个问题。一种简单的解决办法是将驱动器输出端与ADC输入端之间的连接交流耦合起来(如图12所示),以消除ADC驱动器输出端的直流共模电压,并允许向ADC交流耦合一侧注入合适的共模电平。例如,驱动器可能采用5V的单电源,其中 VOCM = 2.5 V ,ADC可能采用1.8V的单电源,应用于ADCCMV的要求输入共模电压为0.9V。

图12. 带交流耦合输出的直流耦合输入
采用偏移型输入共模范围的驱动器一般在采用单电源的直流耦合系统中可发挥出最大优势。其原因在子,输出共模电压通过反馈环路分压,其可变成分可能接近于接地电压(负电轨)。在单端输入情况下,受输入相关纹波影响,输入共模电压甚至更接近负电轨。
采用单端或差分输入和交流耦合或直流耦合的双电源系统,因裕量增加,在两类输入级中都可获得优异的性能。
表2总结了各种输入耦合及电源组合条件下最常见的ADC 驱动器输入级类型。然而,此类选择不一定是最佳选择,每个系统都应进行具体分析。
| 输入耦合 | 输入信号 | 电源 | 输入类型 |
| 任意 | 任意 | 双电源 | 任一 |
| 交流 | 单端 | 单电源 | 中心型 |
| 直流 | 单端 | 单电源 | 偏移型 |
| 交流 | 差分 | 单电源 | 中心型 |
| 直流 | 差分 | 单电源 | 中心型 |
输出摆幅
为了实现ADC动态范围的最大化,输入信号需要达到ADC的满幅度输入范围。然而,驱动ADC应谨慎为上。如果ADC驱动过多,可能损坏输入端;如果驱动不足,又会损失分辨率。对ADC进行满幅度输入范围驱动并不表示放大器输出端必须全范围摆动。差分输出的重大优势之一任于,各输出端仅需摆动传统单端输出端的一半。驱动器输出端可以远离供电轨,结果可减少失真。但是,单端驱动器并非如此。驱动器的输出电压越接近供电轨,放大器的线性度越差,失真越明显。
对于要求毫伏输出电压的应用,请参见表1巾带轨到轨输出端的ADC驱动器,其裕量从数毫伏到数百毫伏不等,具体取决于负载。
图13展示的 ADA4932-1在不同频率下的谐波失真与 VOCM ,其典型输出摆幅为1.2V/轨。输入摆幅为 VOCM与信号 VPEAK 和(1 V)。注意,电压超过2.8V时,失真会急剧增加 (3.8 VPEAK 或比5V供电轨低1.2)。低端时,失真在 2.2 V (–1 VPEAK)时,仍然很低。带宽和压摆率的讨论中会提到类似表现。

图13.ADA4932在不同频率下的谐波失真与VoC(电源电压:5V)
噪声
ADC的缺陷包括量化噪声、电噪声或随机噪声以及谐波失真。作为多数应用中的重要因素,噪声通常是宽带系统中最重要的性能指标。
所有ADC与生俱来都存在量化噪声,具体视位数而定(n); 通过增加位数(n),可减少量化噪声。即使是理想的转换器也会产生量化噪声,因此,人们把量化噪声当作衡量随机噪声和谐波失真的一种基准。ADC驱动器产生的输出噪声应相当于或低于ADC的随机噪声和失真。接下来,我们首先考察ADC噪声及失真的特点,然后探讨如何基于性能来衡量ADC驱动器的噪声。
量化噪声产生的原因在于,ADC将分辨率无限的模拟信号量化成数量有限的离散数据。一个n位ADC拥有 2n 个二进制级。各级之差代表着可以解析的最小差,称为量化级的最低有效位(LSB),简称q。因此,一个量化级为转换器范围的 1/2n。如果可变电压由完美的n位ADC转换,然后变换回模拟信号,再从ADC的输入信号中减除,其余差则表现为噪声。其均方根值为

根据该等式,可以推导出n位ADC在其奈奎斯带宽下的信号-量化噪声比对数(dB)公式(等式22);这是n位转换器可获得的最佳信噪比。

ADC中的随机噪声由热噪声、散粒噪声和闪烁噪声构成,一般比量化噪声大。谐波失真是ADC中的非线性度导致的,会在输出中产生在谐波上与输入信号相关的不良信号。总谐波失真和噪声(THD+N)是ADC的一项重要性能指标,用于将电噪声和谐波失真与接近ADC满量程输入范围的模拟输入进行比较。电噪声在特定带宽范围内积分,该带宽范围包括需要考虑上次谐波的频率。在等式23中,总谐波失真THD包括前五个谐波失真成分,与噪声一起取均方根值。

输入信号为 V1,前五个谐波失真之积为 V2 至 V6。ADC电噪声为Vn.
THD +噪声的倒数,即信噪失真比(SINAD)通常表示为分贝(等式24)。

若以信号-量化噪声比(等式22)代替SINAD,则可定义转换器在信号-量化噪声比等于其SINAD(等式25)的情况下的有效位数(ENOB)。

ENOB也可以SINAD为因子,如等式26所示。

ENOB可用对ADC驱动器的噪声性能与ADC的噪声性能进行对比,以确定其是否适合驱动该ADC。图14所示为一种差分ADC噪声模型。

图14.差分ADC驱动器的噪声模型
一般情况下且 β1 = β2 ≡ β时,八个源对总输出噪声密度的各自贡献分别如27中相应等式所示。

总输出噪声电压密度 Vno, dm如通过计算这些成分的均方根得出。 将这些等式输入电子表格是计算总输出噪声电压密度的最 佳方式。ADI Diff Amp Calculator可快速算出噪声、増益及 差分ADC驱动器的其他有用信息,可从 www.analog.com下载。
现在,可以将ADC驱动器的噪声性能与ADC的ENOB进行比较。比如,增益为2的 AD9445 ADC差分驱动器,采用5V电源和2V满量程输入;该驱动器处理直接耦合宽带信号,占用50 MHz(-3dB)的带宽,以单极滤波器进行限制。根据关于各种条件下ENOB规格的数据表,在奈奎斯特带宽为50 MHz的情况下,ENOB=12位。
ADA4939-1 是一种高性能的宽带差分ADC驱动器,支持直接耦合。就噪声而言,它是驱动AD9445的上好选择。数据表推荐 RF = 402 Ω 且 RG = 200 Ω ,差分增益约为2。这种配置的总输出电压噪声密度为 9.7 nV√Hz.
首先,计算系统的噪声带宽BN,指的是输出噪声功耗与实际滤波器相等的等效矩形低通滤波器的带宽,实际滤波器确定已知常数输入噪声功率频谱密度的系统带宽。对于单极点滤波器, BN 等于 π/2 乘以 3 dB 带宽所得乘积,如等式28 所示。

接下来,计算噪声密度在系统带宽均方根下的积分,以求出输出均方根噪声(等式29)。

根据假设,噪声幅度应呈高斯分布;因引,利用峰峰值噪声(大约在99.7%的时间中,噪声电压会在这些限值之间摆动)的常见士3a限值,峰峰值输出噪声计算方法如下所示:

现在,我们来比较一下驱动器的峰峰值输出噪声与 AD9445 LSB的1LSB,比较的基础是ENOB为12位,且满量程输入范围为2V,如等式31所示。

在12位ENOB下,驱动器产生的峰峰值输出噪声类似于 ADC的LSB;因此,从噪声角度米看,该驱动器是本应用的最佳选择。最终决策必须基于对驱动器及ADC组合的构建和测试。
电源电压
考虑电源电压和电流是缩小ADC驱动器选择范围的简便方式。表1简要总结了ADC驱动器在各种电源电压下的性能,可供参考。电源电压会影响带宽、信号摆幅及 ICMVR。选择差分放大器时,需要衡量各项参数和折衷事项,这是非常重要的。
另一项重要规格参数是电源抑制(PSR)。电源引脚在作为放大器输入端方面所起的作用往往被忽视。电源线存在的任何噪声或者耦合到电源线中的嗓声都可能破坏输出信号。
例如,在 ADA4937-1 上加上50mVp-p、50 MHz噪声的电源。 其50 MHz电源抑制为-70 dB。这就意味着,在放大器输出端,电源线上的噪声将降至16pV左右。在带1V满量程输入的16位系统中,1LSB为15.3 uV;因此,来自电源线的噪声会覆盖1个LSB。
为了改善这种情况,可增加串联SMT铁氧体磁珠LI和L2,以及分流旁路电容C1和C2(见图15)。

图15. 电源旁路
50 MHz下,铁氧体磁珠的阴抗为6022,10 nF (0.01 wF)电容的阴抗为0.32.2。这两个元件构成的衰减器可提供45.5dB的衰减(见等式32)。

除法器衰减与-70dB的电源抑制一起可产生约115dB的抑制性能。结果使噪声降至约90 nV P-P,远远低于1LSB。
谐波失真
频域上低的谐波失真对窄带和宽带系统都非常重要。驱动器中的非线性度会在放大器输出端产生单频谐波失真及多频交调失真产物。
分析噪声一例中用到的方法可以用来分析谐波失真,比较ADA4939的谐波失真与AD944512位ENOB在2V满量程输出下的1个LSB。噪声分析中,一个ENOB LSB为488 µV 。
ADA4939参数表中的失真数据是增益为2时,在不同频率下比较2次和3次谐波得出的结果。表3所示为在增益为2且差分输出摆幅2V p-p时的谐波失真数据。
| 参数 | 谐波失真 (dBc) |
| HD2 at 10 MHz | −102 |
| HD2 at 70 MHz | −83 |
| HD2 at 100 MHz | −77 |
| HD3 at 10 MHz | −101 |
| HD3 at 70 MHz | −97 |
| HD3 at 100 MHz | −91 |
数据显示,谐波失真随频率而增加,且在目标带宽(50 MHz)下,HD2表现比HD3差。谐波失真产物的频率高于目标频率,因此,可通过限制系统频带来降低其幅度。如果系统在50 MHz下采用"砖墻式"滤波器,则只需考虑高于 25 MHz的频率,因为该滤波器消除了频率更高的全部谐波。 然而,系统的最高带宽设为50MHz,因为所用滤波器可能无法充分抑制谐波,失真产物可能以杂散信号进入信号带宽。图16展示了当输出为2Vp-p时,ADA4939在不同电源电压下的谐波失真与频率的关系。

图16.谐波失真与频率的关系
相对于2V p-p的输入信号,50MHz下的HD2约为-88dBC。 为了比较谐波失真与1 ENOBLSB,必须将该电平转换成电压,如等式33所示。

失真产物仅为80pV p-P,相当于1 ENOB LSB的16%。因此,从失真角度来看,ADA4939是AD9445 ADC驱动器的良好选择。
由于ADC驱动器属于负反馈放大器,其输出失真取决于放大器电路中的环路增益量。负反馈放大器的内部开环失真下降1/(1+LG),其中,IG表示可用环路增益。
放大器的输入(误差电压)乘以一较大正向电压增益A(S),然后通过反馈因子阝,反馈到输入端,在此调整输出以减少误差。因此,这类放大器的环路增益为A(S) x B;随着环路增益(A(s)、B,或者两者兼而有之)的减少,谐波失真会增加。积分器之类的电压反馈放大器设计用于在直流及低频下产生大A(s),然后在指定高频处朝着单位1星1/滚降。随着A(s)的滚降,环路增益会减小,失真会增加。可见,谐波失真为A(s)的倒数。
电流反馈放大器可将误差电流用作反馈信号。误差电流乘以一较大正向跨阻T(s),将电流转换成输出电压,然后通过反馈因子1/RF,将输出电压转换成反馈电流,以减少输入误差电流。因此,理想电流反馈放大器的环路增益为 T(s) × (1/RF) = T(s)/RF。与A(s)类似,T(s)具有较大的直流值,会随着频率增加滚降,结果减少环路增益、增加谐波失真。
环路增益同时与反馈因子1/R;有直接关系。理想电流反馈放大器的环路增益并不取决于闭环电压增益,因此,谐波失真性能不会随着闭环增益的增加而下降。在现实电流反馈放大器中,环路增益在一定程度上取决于闭环增益,但依赖程度远低于电压反馈放大器。这样,对于要求高闭环增益和低失真的应用来说,电流反馈放大器(如ADA4927)优于电压反馈放大器。
图17展示了在闭环增益增加时,ADA4927失真性能的情况。

图17. 失真与频率和增益的关系
带宽和压摆率
带宽和压摆率在ADC驱动器应用中显得尤其重要。一般地,小信号带宽为器件的带宽,而压摆率则旨在衡量放大器输出端在大信号摆幅下的最大变化率。
与ENOB类似,有效可用带宽(EUBW)描述的是带宽。许多 ADC驱动器和运算放大器都声称具有很宽的带宽,但并非全部带宽都能派上用场。例如,-3dB带宽是常规的带宽衡量方式,但并不表示全部-3dB带宽都是可用的。-3dB带宽的幅度和相位误差可以比实际的截止频率提前十倍出现。确定可用带宽的一个好办法是查阅数据手册中的失真图。
图18显示,为了使二次和三次谐波维持在大于-80 dBc的水平,则不能在高于60 MHz的频率下使用ADC驱动器。由于应用各不相同,应根据系统要求来选择带宽充足、失真性能良好的驱动器。

图18.ADA4937电流反馈ADC驱动器的失真曲线
压摆率(一种大信号参数)指在不出现过量失真的情况下,放大器输出端可以对输入端进行跟踪的最大变化率。考虑压摆率下的正弦波输出。

零交越下,等式34的导数(变化率)即最大变化率力

where:
dv/dt max 为压摆率。
VP 为峰值电压。
f 为全功率带宽(EPBW)。求解FPBW,

可见,在选择ADC驱动器时,必须考虑增益、带宽和压摆率(IFPBW),以确定放大器能否满足应用需要。
稳定性
差分ADC驱动器稳定性考虑与运算放大器相同。关键参数是相位裕量。特定放大器配置的相位裕量可根据数据手册得到,然而,在现实系统中,PCB电路板布局存在的寄生效应可能大幅降低相位裕量。
负电压反馈放大器的稳定性取决于其环路增益(即A(S)×B)的量和符号。差分ADC驱动器拥有两个反馈因子,因而比典型的运算放大器电路要复杂一些。环路增益出现在等式 7和等式8的分母中。等式37描述的是未匹配反馈因子下的环路增益 (β1 ≠ β2)。

当反馈因子不匹配时,有效反馈因子为两个反馈因子的平均值。当二者相匹配且定义为B时,环路增益可简化为 A(s) × β。
为了使反馈放大器保持稳定,其环路增益不得等于-1或其等效值,即相移-180°时幅度为+1。对于电压反馈放大器而言,在其开环增益频率坐标图上,环路增益等于1(即0dB)的点正好是A(s)的量等于反馈因子倒数的点。对于基本的放大器应用,反馈纯粹为电阻式,不会在反馈环路中产生相移。当反馈因子相匹配时,独立于反馈因子倒数 1 + RF/RG的频率通常称为噪声增益。如果将以分贝为单位的不变噪声增益画在与开环增益A(s)相同的坐标图上,则两条曲线相交处的频率为环路增益为1或0dB之处。A(s)在该频率下的相位与-180°之差被定义为相位裕量,为了运行稳定,其值必须大于或等于45°。
图19展示了ADA4932 RF/RG = 1 (噪声增益=2)时的单位环路增益点和相位裕量。

图 19.ADA4932开环增益量和相位与频率的关系
仔细考察图19可以发现,当噪声增益为1(各环路反馈100%)时, ADA4932-2 的相位裕量约为50°。虽然使ADC驱动器运行于零增益下是不切实际的,但观察表明,ADA4932可在小数差分增益(例如,RF/RG = 0.25,噪声增益=1.25)下稳定运行。但并非所有差分ADC驱动器皆是如此。在所有ADC驱动器的数据手册中,可以看到最小稳定增益。
电流反馈ADC驱动器的相位裕量也可根据开环响应来确定。电流反馈放大器采用的不是正向增益A(s),而是正向跨阻T(s),以误差电流作为反馈信号。带匹配反馈电阻的电流反馈驱动器的环路增益为 T(s)/RF:因此,当 T(s) = RF时,电流反馈放大器环路增益量等于1(即0dB)该点可在开环跨阻与相位关系坐标图上轻松找到,其方法与电压反馈放大器相同。对电阻与1k2之比作图,可在对数坐标图上表示电阻。图20展示了ADA4927电流反馈差分ADC驱动器在 RF = 300 Ω 时的单位环路增益点和相位裕量。

图20.ADA4927开环增益量和相位与频率的关系
环路增益为0 dB,3002反馈电阻水平线与跨阻量曲线相交于此。在此频率下,T(S)的相位约为-135°,结果得到+450的相位裕量。相位裕量和稳定性与R;同向升降。电流反馈放大器应始终采用相位裕量充裕的纯电阻式反馈。
PCB电路板布局
在设计稳定的ADC驱动器时,这种思想必须在PCB电路板上实现。电路板中的寄生元件会导致部分相位裕量损失,因此必须将此类元件减至最少。需要特别注意的是负载电容、反馈环路电感和求和节点电容。各个此类寄生电抗都会增加反馈环路中的滞后相移,由此导致相位裕量减少。如果PCB电路板布局不当,设计本身即可损失20°或以上的相位裕量。
在电压反馈放大器的情况下,最好采用小的 RF ,以减少因 RF 与求和节点电容形成的极点导致的相移。如果需要采用大 RF ,可在各反馈电阻上利用小电容 CF;来补偿该电容,小电容的值应使 RF × CF 等于R与求和节点电容之积。
PCB电路板布局实际上是设计流程的最后步骤之一。不幸的是,尽管高速电路的性能高度依赖于布局,这同时也是设计过程中最易被忽视的步骤之一。设计不当的布局可能使性能大打折扣,甚至使其失去效用。虽然此处不可能涵盖高速PCB电路板设计的各个方面,但我们将讨论几个关键话题。
寄生元件会牺牲高速电路的性能。寄生电容由元件焊盘和布线与接地层或电源层形成。无接地层的长布线会形成寄生电感,可能在瞬态响应中导致振铃振荡或其他不稳定行为。寄生电容在放大器的求和节点处尤其危险,因为这种电容会在反馈响应中产生极点,导致峰化和不稳定。一种解决办法是确保在电路板各层中,ADC驱动器支架及反馈元件焊盘下方不存在接地层和电源层。
为了减少不良寄生电抗,应尽量缩短所有布线的距离。 FR-4上的外层500 PCB电路板布线会贡献大约2.8pF/英寸和7nH/英寸的寄生电感。而内层502布线则会使此类寄生电抗增加约30%。另需确保长的走线下方有接地层,以减少布线电感。尽量缩短布线距离、减小其大小有助于降低寄生电容和电感,有利于维持设计的完整性。
电流旁路是电路板布局中的另一个关键;务必确保电源旁路电容以及 VOCM旁路电容位于尽量接近放大器引脚之处。另外,在电源层采用多个旁路电容有助于确保为宽带噪声提供一个低阻抗路径。图21所示为一种典型的差分放大器示意图,其中含有电源旁路,输出端带一低通滤波器。该低通滤波器用于限制进入ADC的带宽和噪声。理想情况下,电源旁路电容回路应靠近负载回路:这样有助于减少接地层中的循环电流并提高ADC驱动器的性能(参见图22)。

图21.带电源旁路和输出低通滤波器的ADC驱动器
接地层以及广义接地是个内容丰富的复杂话题,超出了本应用笔记的范围。但是可考虑以下关键点(见图22):
- 只在一个点上连接模拟地和数字地。这样可减少模拟电流和数字电流在接地层中的交互作用,避免其在系统中产生噪声。
- 将模拟电源接入模拟电源层,将数字电源接入数字电源层。
- 对于混合信号IC,将模拟地回路接入模拟接地层,将数字地回路接入数字接地层,并仅用一小连接将两个接地层相连,以减少数字电流与模拟电流的混合(见图23)。

图22.元件侧面(a)

图 23. 电路侧面(b)

图24. 混合信号接地
有关高速印刷电路板(PCB)布局的详情,请参阅《高速印刷电路板布局实用指南》,网址: www.analog.com。
本应用笔记所含信息旨在帮助大家思考在设计ADC驱动器时必须考虑的各种因素。深入了解差分放大器并从设计之初即注意ADC驱动器设计细节,有利于减少将来的问题,降低风险,确保设计的鲁棒性。

