TNJ-079: ADC で 1Hz ノイズ電力密度を得るためのランダム・ビット発生回路と密度計算式
はじめに
これまで 2冊の技術ノート(TNJ-077, TNJ-078)で ADC(Analog to Digital Converter)の NF について考えてきました。今回以降はさらにその続きとなる、「AD変換結果で 1Hz ノイズ電力密度の絶対値をどうやって得るか」という話題に突入してみたいと思 います。とくに今回の技術ノートでは、AD変換結果を 1Hzノイズ電力密度絶対値レベルへ実験的に校正する方法を示し、次の技術ノートでは AD 変換結果自体から 1Hz ノイズ電力密度絶対値レベルを直接計算する方法を示します。
その今回は、絶対基準器となるノイズ発生回路を作り、そのレベルを測定してみます。それでも測定のみ(場当たり的?)に依らずに、その 1Hz 電力密度を「パーセバルの定理(Parseval’s theorem)」[1]という理論ネタを用いて、理論的に導出してみたいと思います。この導出と結果は、他ではなかなか見ることのないご提供ネタに仕上がったのでは(実は次回の絶対レベル計算方法も、なのですが)、と勝手に思いあがったりしていました。しかしそれは、次の金木犀ネタとは真逆な意識であることに気づき、恥じてしまう私でありました…。
金木犀かおる秋、空高く
生まれてから今まで、毎年、この時期になると、濃密かつ高貴に香る小さく黄色い花が咲いていることに、多くのところで気づかされます。先日もウォーキングに出かけるとその香りがし、「ああ、ここにもあるんだな」と、なんだか理由もなくほっとする気持ちがしました。齢を重ねるにしたがい、自然の、四季のうつろいへの感受が強まったのか、感受すべき、享受すべきと思うようになったのか、そのような四季の自然のワン・シーンにも気持ちが向くようになった気がします。


この濃密かつ高貴に香る小さく黄色い花、それは金木犀(きんもくせい)。金木犀の花の香りに誘われ、すがすがしい青い空を背景にその金木犀の写真を撮ってみました(図 1)。
ちょっと気になり、金木犀の花言葉を調べてみると「謙虚」[2] とあります。その素晴らしい香りに対して、花が小さく控えめだということが由来のようです。齢を重ねるにしたがい、謙虚になれなくなりつつあるのかなと思うこの頃。もう一度、金木犀の花を見上げつつ、「謙虚…ねぇ…」とその齢のところで立ち止まり、ひとり想いに耽って(ふけって)みるのでした。
校正基準となるノイズを発生させる PRBS デジタル回路
校正基準レベルとなるノイズを発生させる回路として PRBS デジタル回路を用います。PRBS は Pseudo Random Binary Sequence の頭文字をとったもので、疑似ランダム・パターンなどと日本語では呼ばれます。
ところで「疑似」、Pseudo はどのように発音するのでしょうか。私は「プシュード」と呼ぶものだと長く思っていました。「プセウドゥ」なのかな?とも思っていました。しかし、あらためて調べてみると「スードゥ」なんですね(ネット辞書は発音例もあるのでありがたいです)。P は発音しないのですね…。
さて、ここでは 16 ビットの PRBS を発生させるための「原始多項式」

というものを用います。これで構成された回路は、図 2 のように、フリップ・フロップを 16 個と、XORを 3 個用いたものになります。
x のべき乗の指数に相当する順番のフリップ・フロップから信号を取り出し、それらを XOR して入力にフィードバックします。この回路を LFSR、Linear Feedback Shift Register とも呼びます。これにより 216-1 ビット、65535 ビットで繰り返す疑似ランダ ム・パターン、PRBS-16 を構成できます。
この回路を図 3 のような FPGA(Field Programmable Gate Array; といっても実際は CPLD; Complex Programmable Logic Device)に書き込みます。余談ですが、この基板は「CPLD キット」であり、相当前にネットで探して見つけ、欧州から直輸入したものです(って、このネット時代、そんなに大した行為ではありませんが)。CPLD や SOP の SRAM 以外は自分ではんだ付けしま した(笑)。CPLD は電源投入時にプログラム書き込みなしに即動作するので、こんな実験用にはとても便利です。CPLD は Xilinxの XC95144が使われています。144マクロ・セルでは大したこともできませんが…。
本題に戻りましょう(汗)。ここに 10 MHz のクロックを供給すれば、10 Mbps の PRBS-16 となり、10 MHz をヌル点(谷)とした sinc 形状の広帯域なノイズ状のスペクトルが得られます。








この回路で発生させた 10Mbpsの PRBS-16のスペクトルを図 4 に示します。このプロットはスパンが 50MHzであり、10MHzステ ップでヌルができていることが分かります。
この sinc 形状のスペクトルのうち、低域の周波数、たとえば 10Mbps に対して 1MHz 以下の周波数であれば、その周波数領域ではスペクトルが一定レベルの「ホワイト・ノイズ」とみなすことができます(疑似ノイズになります)。図 4 をご覧いただいても、1MHz は左から 2%のところであり、その領域はほぼフラットになっていることが分かりますね。
出力振幅レベルを求める(テブナンの定理の出番)
設計した回路は 5V CMOS ですが、実際に CMOS出力の振幅レベルを実測してみると 4.8V でした。以降はこの数値、4.8V を用いて説明していきます。
この 4.8V の CMOS出力を図 5 のように 1kΩと 75Ω, 180Ωで分圧し、レベルを低下させるとともに、ADC である負荷側からこの回路を見たインピーダンスが 50Ωになるように構成しています。
ここでテブナンの定理を用いて、等価内部電圧源の大きさと出力抵抗の大きさを計算してみます。50Ω負荷を接続しない条件での出力電圧は

出力抵抗は

これから図 6 のように図 5 の等価回路を得ることができます。 ADC 側(測定系側)ではこれを 50Ωで終端して受けます。このとき終端抵抗の端子電圧は、式(2)の半分の 120.5mV になります。






PRBS-16 疑似ノイズの 1Hz 電力密度を得る
スペクトルを観測し 1Hz 電力密度レベルを測定してみる
実際に 2 種類のスペクトラム・アナライザで、PRBS-16 で発生させた疑似ノイズのノイズ 1Hz 電力密度を実測してみました。これは実測によりノイズ基準値を得るという考え方です。なお以降に示す、パーセバルの定理を使った理論値は-78.4dBm/Hz になります。
スペアナは 1Hz の電力密度を読み出すノイズ・マーカにし、100 回 rms 平均化を行っています。スペクトルが一定とみなせる低域の周波数 500kHz において、図 7 の 89410A では-78.3dBm/Hz、 図 8 の 8560B では-78.5dBm/Hz となっています。それぞれほとんど同じ値です。この測定値をもとに、任意の信号の AD 変換データを FFT した結果を 1Hz 密度電力として校正することができます。
なお、スペアナでのマーカ・リードアウトには誤差があるので注意してください(これも基準電力となる信号源を用意し、それと比較し校正しておくとよいです)。
数式から PRBS-16 疑似ノイズの 1Hz 電力密度レベルを計算してみる
つづいて数式から PRBS-16 疑似ノイズ 1Hz 電力密度を求めてみましょう。この計算は「パーセバルの定理」を利用して導出したものです。
導出方法は以降に詳解しますので、ご興味あるかたはご覧ください。
さて、50Ωの負荷抵抗に±1V の矩形波、ビットレート𝐵𝑅 [bps] の PRBS 疑似ノイズが加わったとき、PRBS のスペクトルがフラットになる低域での、その 1Hz 電力密度𝑃𝑆Dは

になります。実際の振幅ピーク・ツー・ピーク・レベルを𝑆 [Vp-p]とすると、1Hz 電力密度は、さきの𝑃𝑆D(1V)から

として20 log (𝑆/2)で補正されます。1/2 するのはピーク・ツー・ピークを±x V(バイポーラ)に直す(条件をそろえる)ためです。
この例ではビットレート 𝐵𝑅 = 10Mbpsですので、まず±1V の矩形波で考える𝑃𝑆D(1V)は式(4)から

と計算できます。
図 5 の「1kΩと 75Ω, 180Ωで分圧」した出力の実際の振幅レベルは、図 6 のように開放端で 241mVp-p、50Ωの負荷抵抗に加わ った場合(50Ω終端の状態)で半分の 120.5mVp-p となり、この振幅レベルでの補正値は式(5)の第 2 項から

これで PRBS-16 疑似ノイズ源による 1Hz 電力密度基準レベルが得られた
結果として-54.0 - 24.4 = -78.4dBm/Hz が得られます。これはさきの実測値とほぼ同じものですね。
これでスペクトラム・アナライザによる実測と式、それぞれで基準値となる PRBS-16 疑似ノイズ源によるノイズ 1 Hz 電力密度基準レベルが得られました。この PRBS 疑似ノイズ源を測定したものが「-78.4dBm/Hz」だとして目的の信号の測定値を補正すれば、任意の信号の AD 変換データを FFT した結果を校正し、 1Hz 密度電力を得ることができるわけです。
PRBS 疑似ノイズ源の信号を AD 変換/FFTした結果を校正してみる
それでは実際に PRBS 疑似ノイズ源出力を 50Ω終端して、AD 変換したデータを FFT した値を校正してみましょう。これにより任意信号の 1Hz密度電力も得ることができます。さきの PRBS-16 疑似ノイズ源を 50Ω終端して、AD変換しデータを取り込みます。
使用した ADC は、最高 5Msps、18 ビットの AD7960 [3]です。 5Msps で 65536 ポイントのデータを取得しました。AD7960 をご紹介しておきましょう。
AD7960 18 ビット AD コンバータ、5 MSPS、差動入力、 PULSAR®
https://www.analog.com/jp/ad7960
【概要】
AD7960は、18ビット、5Mspsの電荷再配分式逐次比較型(SAR)の A/D コンバータ(ADC)です。SAR アーキテクチャのため、ノイズと直線性の両方に関して並外れた性能が達成されています。AD7960 は、低消費、高速、18 ビットのサンプリング ADC、内部変換クロック、それに内部のリファレンス・バッファ回路を内蔵しています。(後略)
取得した 5Msps 65536 ポイントのデータにハン(Hann)窓と呼ばれる窓関数をかけて、単純に FFT した結果が図 9 のプロットになります。
しかしこのプロットでは、レベル変動が-64 dB から-90 dB と、非常に大きいことが分かります。これでは「ノイズ 1 Hz電力密 度は一体幾つ?」という答えを得られるものになっていません。
FFT 処理で得られた答えがそのまま 1Hz 電力密度にはなっていない(だいぶ厄介だ…)
なお FFT というものは、その答えはそのまま 1Hz密度にはなりません。次の技術ノートでそのあたりを(この ADC のノイズ 1Hz 電力密度の算出を例にして)詳しく説明しますが、結構そこに辿りつくのは面倒なのです。




ぱっと思い浮かぶことは「FFT 全長を 1sec にすればよいのでは?」ということですが、それだけでは上手くいきません。
算出は別途ご紹介するとして、ここではここまで得られた PRBS 疑似ノイズ源の密度電力の値を校正標準として、FFT 処理結果を校正してみます。
FFT 処理の結果を 1Hz 電力密度になるように校正すればよい
図 10 はこの FFT した結果を、「電力の足し算」つまり rms 平均化で 100 ポイント移動平均をしてみたものです。ここでの移動平均処理は、オール 1 の 100 タップの FIR(Finite Impulse Response )フィルタとの畳み込みで計算させています。 MATLAB でこんな風に計算しています。
noisepowerbin = (abs(noisefft)).^2 / 50;
noisepowerbin = conv(noisepowerbin, ones(100, 1)) / 100;
ここで noisefft は単純に FFT した結果、noisepowerbin はそれを 50Ωの負荷抵抗に加わるエネルギとしたもの、下の行はオール 1 の 100 タップの FIR フィルタと畳み込み計算をしたものです(得られた結果は数値数が増えるので数をそろえる必要があります)。いまだ若干の変動はありますが、レベル変動がかなり低下していることが分かります。
実測と計算で得られた PRBS 疑似ノイズ源による電力密度の値は-78.4 dBm/Hz でした。この PRBS 疑似ノイズ源を AD 変換し、 FFT して移動平均した結果が-78.4 dBm/Hz に相当するのだとして、FFT 結果のレベルを校正すればよいのです。
以降で目的とした信号の 1Hz 電力密度を実測する場合には、ここで得られた校正値で数値を補正すればよいのです。
ここまででこの技術ノートの第一の目的は達成です。
AD 変換での折り返しの影響は?
前々回の TNJ-077、前回の TNJ-078で広帯域に分布するノイズ成分が AD変換により折り返され、1st Nyquist Zone(一般的に「ナ イキスト帯域」と呼ばれるもの)に落ち込んでくる、というお話しをしました。またアンチエイリアシング・フィルタを用意することで多くの場合は、その問題は表に出てこないとも説明しました。
今回の AD7960 ではこれはどう考えればよいのでしょうか。
PRBS-16 のビットレートと AD7960 のサンプル・レートがよい塩梅(あんばい)になっている
「あんばい」とは良い塩加減のことらしいですね(笑)。まあ、それはよしとして、今回の実験ではアンチエイリアシング・フィルタを用意していません。しかし実験結果が正しく理論値とあうのは理由があります。
PRBS-16 のビットレートは 10Mbps で、図 4 のように 10MHz のところにヌルがあります。一方で AD7960 のサンプリング・レ ートは 5MHz であり、図 4 の PRBS-16 のスペクトルは 5MHz を中心に折り返されます。つまり測定している 500kHz あたりの帯 域では、PRBS-16 の 2nd Nyquist Zone にある、10MHz のヌルの少し手前(9.5MHz 付近)が折り返されることになります。この レベルは十分に低く、本来の 500kHz のスペクトルのレベルに影響を与えないようになっているのです。
PRBS-16 のビットレートと ADC のサンプル・レートが塩梅よくない場合は
いつもこのように塩梅よい条件に設定できるものではありません。これがうまく設定できない場合はアンチエイリアシング・フィルタを用意して、折り返しとなるスペクトルの周波数成分を除去する必要があります。
理論式の考え方(理論的背景)
上記で式(4)から式(7)にかけて 1Hz 電力密度レベルの計算方法を示しました。以降ではこの理論的背景を示してみます。
図 11 に示すような、10Mbps, 1V の矩形波 1 ビット「のみ」の孤立波をまず考えます。これを𝑠(𝑡)として式で表すと
これをフーリエ変換(角周波数軸に変換)したものは






ここでωは角周波数(ω = 2𝜋𝑓)、𝑇はパルス幅の 1/2 (𝑇 = 50ns)です。これを図示すると図 12 となります(この図は周波数表現での表示)。ここで以下のようなパーセバルの定理(Parseval’s theorem)

を用います。難しそうにも見えるのですが、「時間軸で見た 1Ω負荷に加わる全エネルギ(単位時間内で信号が収まれば「電力」)は、周波数軸で見た全エネルギ(同じく「電力」)と等しい」という、至極もっともと言える定理です。
また図 11 の矩形波は 1 ビットのみです。そこで生じるエネルギは有限ですから、それが周波数軸で表されただけと考えれば腹落ち感があるものと思います。
さて、上記の式(10)の右辺は𝜔の関数なので、周波数𝑓として考えたいため、ω=2𝜋𝑓で置換積分してみます。まずこれを微分し

を得ます。つづいて式(10)の右辺から

どうでもいい話ですが、角周波数ωに関連して「係数2𝜋」がこのような数式ではよくでてきます。しかし係数2𝜋はここでは消えてしまうため、「係数2𝜋」とは人為的に考えられた「人造物」であり、自然界の振る舞いとしては「円周の一周は 1」になっていることに気づかされます(笑)。
この計算は「自乗して電力相当値にして積分する」という考え方で、図 13 のイメージです。これから上式の左辺、右辺共々

と表されます。ここで考えるべきは「実際の信号スペクトルの 500kHz の周波数における 1Hz 帯域」なので

とすれば、

の範囲と

の範囲です。信号解析においてはプラス・マイナス両方の周波数で考える必要があるからです(図 14 に概念を示します)。
そうするとこの電圧レベル 1V、10Mbps 矩形波 1 ビットにより 1Ωの負荷抵抗に生じるエネルギ・スペクトルの𝑓𝑑± = ±500 kHz の 1Hz 帯域におけるエネルギ密度は
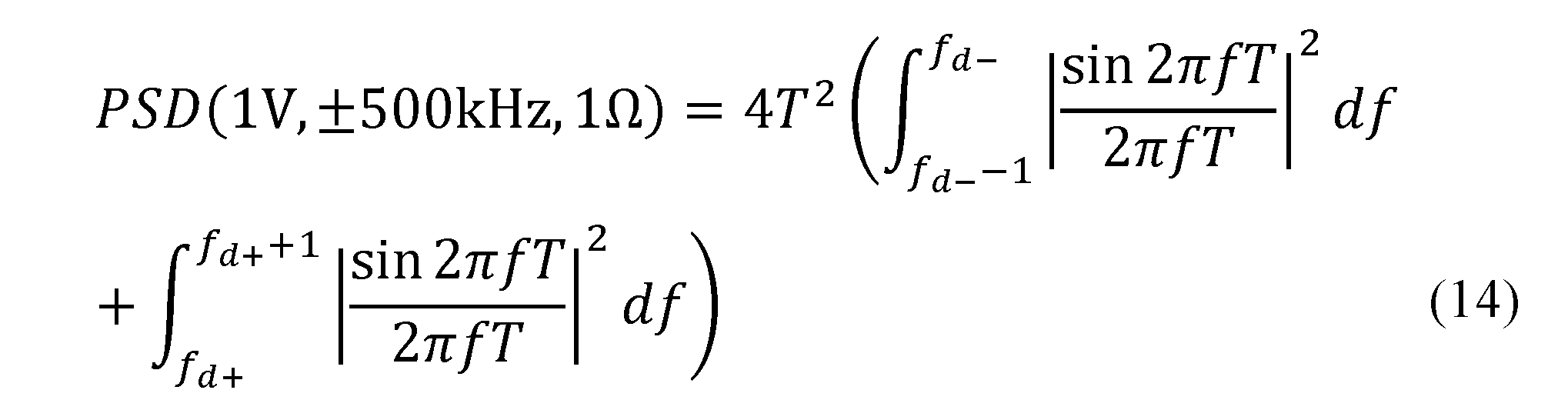
ここで当然ながら±500kHz とそこから 1Hz 離れた周波数の信号スペクトル・レベルは、図 15 のようにほぼ同じであり、たとえば𝑓𝑑+ = +500kHz, 𝑇 = 50nsにおいてその大きさは

𝑓𝑑−も同様です。なお電圧レベルは 1V での計算です。先の積分式[式(14)]から









これから

これは 1Ωの負荷抵抗に生じる、パルス全長 10ns、1V 矩形波 1 ビット分の 1Hz 電力密度なので、50Ωの負荷抵抗では、電力計算の式

から、図 16 のように電力は 1/50 となり、

これを dBm/Hz に直すと-124dBm/Hz になります。これがパルス全長 10ns、1V 矩形波 1 ビット分の 500kHz における 1Hz 電力密度となります。1sec あたりの全電力は 10Mbit分(1千万ビット個数分)として

となり

が得られます。これが「50Ωの負荷抵抗に生じる、10Mbps(パルス全長 10ns)、0V-1Vの PRBS 疑似ノイズ信号の 1Hz 電力密 度」です。
ここから先は式(4)からの展開になるわけです。
PRBS 疑似ノイズ全体で孤立波の電力のビット数倍として計算できる理由は?
式(18)以降で、「パルス全長 10ns の単一パルス(孤立波)の電力を、そのまま一千万倍する」という説明をしました。ここで疑問が沸くのではないかと思います。それらは「PRBS は 0V と S [V]の間を変化するランダム信号だが、1 パルスの電力をそのまま 1 千万倍していいの?」「ビットが 0V のときが確率的に 50%あるが、ビットが 0V ならエネルギは生じないはず。この 50%の率を考慮しなくていいの?」。また「振幅はどう考えるの?」というものかと思います。
これはここまで検討を図 17 のように考えてきたからです。式(8) では、10Mbps, 1V の矩形波 1 ビット「のみ」の孤立波𝑠(𝑡)とし ていました。連続ビット列として考えると、同図の上のように +1V と-1V の間を変化する電圧変化となります。これが式(4)になります。


電圧が+1V のときの電力は𝑉2/𝑅から𝑅 = 1として考えると 1W であり、電圧が-1V のときの電力も(自乗されますから)1Wとなり、全てのビットごとで式(17)に相当する電力が生じていることになります。
この定義から、「1Vのパルスの電力をそのまま 1 千万倍」ということになるわけです。
つづいて実際のビット信号の振幅を考えます。式(5)の説明「実際の振幅ピーク・ツー・ピーク・レベルを𝑆[Vp-p]とする」を用いると、ビット信号は 0V と𝑆[V]の間を変化します(図 17 中央)。「ここではビットが 0Vのときがあるじゃん」と思われるかもしれませんが、実際はこれを DC カットすれば、PRBS パターン信号がその振幅の中央を 0Vとして変化するようになります。それによりレベルが+𝑆/2 [V]と−𝑆/2 [V]の間を変化する電圧変化となります(図 17 下)。すなわち信号を「±𝑆/2 [V]のバイポーラ信号」として考えており、そのため式(5)では 1/2 の係数がかかっていることになるのです。
まとめ
150 円のりんご 1 個と 180 円のレモン 1 個を買えば、支払額は 330 円です。150 + 180 = 330 と式では書けます。実際と数式は当然ながら等しくなります。
しかし PRBS 信号源から発生させた、振る舞いのよく分からないノイズの電力(1Hz 密度)を実測してみて、それと計算式とのつじつまを合わせることには、「きちんと合うのかな?」とはじめはかなりの不安がありました。
しかしパーセバルの定理を使うと、コンマ dB のオーダまできちんと合うことに、書いている本人としても驚きを隠しえませんでした。いつものとおり、考えながら執筆する WEBラボ(というか、その前にアナログ技術セミナーのネタとして考えていたのですが)なのでありました。
次回は、今回のような既知の PRBS 疑似ノイズ信号源を測定した実測結果を基準にする、という現場的アプローチではなく、 FFT した結果からそのまま 1Hz 電力密度を求めるという、より高尚(?)な展開に突入してみたいと思います。そこでもちゃんと答えが出たのですが、その検討結果はさらに 2 冊の技術ノートを生むという、細胞分裂的に探究が進んでいくストーリーをも生み出したのでした…。
著者について
デジタル回路(FPGAやASIC)からアナログ、高周波回路まで多...