AN-924: Digital Quadrature Modulator Gain
Introduction
Digital quadrature modulators appear in a number of communications and signal processing ICs. This application note explains the basic building blocks of a digital quadrature modulator and provides an analysis of the gain through the modulator for three types of input signals.
The generic digital modulator consists of a pair of digital multipliers and a digital adder, configured as shown in Figure 1. Generally, the binary numbers associated with the data paths all have the same numeric range, namely ±1. This applies to the input (I, Q, and carrier), output (Y), and intermediate data paths. An N-bit bus width is shown in the diagram for the sake of generality, where the N bits represent fractional numeric values between −1 and +1.

Figure 1. Digital Quadrature Modulator Functional Diagram.
Of the four inputs, two are dedicated to processing the digital carrier signal, which is an N-bit quantized representation of the sine and cosine waves that constitute a quadrature carrier. By definition, the carrier has separate cosine and sine components, both of which oscillate (numerically) at the carrier radian frequency, ωC (where ωC equates to 2πfC, with fC denoting the more familiar units of cycles per unit time). The other two inputs (I and Q) are used for processing a digital, N-bit quantized, baseband signal. The I and Q labels are shorthand notation for the in-phase and quadrature components, respectively, of the baseband signal. The output, Y, is an N-bit quantized digital representation of the baseband signal upconverted to the carrier frequency (fC).
The relationship between the input and output signals can be expressed as a function of time, as shown in Equation 1.
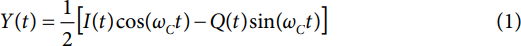
The carrier signal is time dependent by definition as indicated by the t term in the arguments of the sine and cosine functions. The Y, I, and Q terms have been assigned t arguments as well, indicating that their values can also be time dependent. The scale factor of ½ is a consequence of using the same number of bits at both the input and output of the adder. The reason is that the sum of the two N-bit multiplier outputs actually requires N + 1 bits to represent the full range of the summed results. However, the act of constraining the output of the adder to only N bits means that the least significant bit of the N + 1 bit result must be discarded. The act of truncating the sum to N bits results in an intrinsic 50% loss through the adder, hence the scale factor of ½ that appears in Equation 1.
An analysis of the output signal, Y(t), for three different types of I and Q input signals follows. The input signal types under consideration are
- A static input signal
- A nonquadrature sinusoidal input signal
- A quadrature sinusoidal input signal
The following analysis is aided by the trigonometric identities given by Equation 2 and Equation 3. In addition, the formula given in Equation 4 is useful for quadrature signal analysis. It relates a quadrature expression (the left side) to a cosine function (the right side). Of particular interest is the application of Equation 4 to Equation 1, which produces an alternative form for Y(t), as shown in Equation 5.
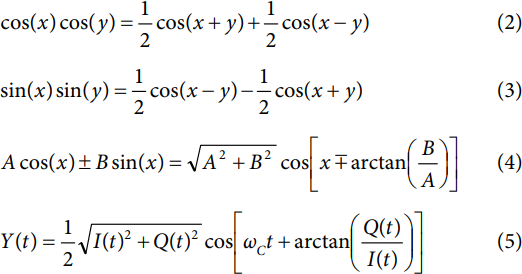
Static Input Signal Analysis: I(t) = D and Q(t) = E
In this case, the I and Q input signals are not time dependent, but they are the static numeric values given by D and E, respectively. D and E are assumed to be fractional values between 0 and 1, inclusive, implying that they represent a fractional portion of the maximum possible peak input value. Based on Equation 5, Y(t) is expressed a
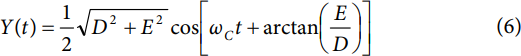
Note that the argument of the cosine function in Equation 6 contains only a single frequency component (ωC). This implies that the output signal is a single tone with the same frequency as the carrier signal. The phase of the output signal, however, is advanced by the radian angle, arctan(E/D), relative to the phase of the cosine component of the quadrature carrier input signal. Furthermore, the amplitude of the output signal is dependent on the vector sum of D and E. For the unique case in which D and E are the same numeric value (that is, D = E = k (0 ≤ k ≤ 1)), Y(t) reduces to

It is instructive to consider the specific case of k = 1; that is, the I and Q inputs are static full-scale values. When k = 1, the peak value of Y(t) is √2/2. This represents a gain of −3 dB relative to the maximum possible peak output value of 1. The normalized output power is (√2/2)2 = ½, or −3 dB relative to the maximum possible output power of (1)2 = 1.
Nonquadrature Sinusoidal Input Signal Analysis: I(t) = A × cos(ωBt) and Q(t) = B × cos(ωBt)
In this case, the I and Q input signals are sinusoids. Both sinusoids possess an arbitrary baseband radian frequency, ωB, with no relative phase offset (that is, both signals are in phase with each other). Furthermore, the I signal is scaled by the constant A (0 ≤ A ≤ 1), and the Q signal is scaled by the constant B (0 ≤ B ≤ 1). Based on Equation 5, the output signal is expressed as
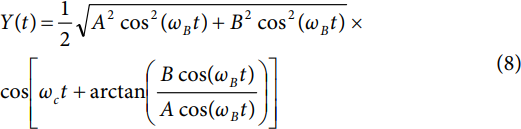
This simplifies to
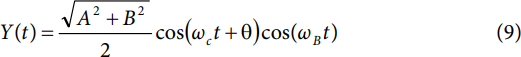
Note that, similar to the static input signal case, the carrier exhibits a constant phase shift given by θ = arctan(B/A).
Application of Equation 2 to the form of Y(t) in Equation 9 leads to
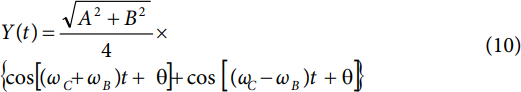
Notice that Y(t) consists of two cosine functions. One of the cosine functions contains the radian frequency term ωC + ωB, and the other contains the radian frequency term ωC − ωB; however, both functions exhibit a phase shift of θ = arctan(B/A). Thus, Y(t) is composed of two tones, both offset from the carrier frequency (fC) by the baseband frequency (fB). Furthermore, each tone is scaled in amplitude by the quantity

It is instructive to consider the case of A = B = 1; that is, the I and Q signals have peak values that span the full-scale input range. In this case, the peak value of each output tone becomes √2/4 and the phase offset (θ) becomes π/4 radians. Note that a peak value of √2/4 represents a gain of −9 dB relative to the maximum possible peak output value of 1. However, the fact that the two tones are at different frequencies means that their combined amplitude reaches a peak value of twice that of either tone considered separately (regardless of the value of θ). Therefore, the peak amplitude of Y(t) is 2(√2/4) = √2/2. This represents a gain of −3 dB relative to the maximum possible peak output value of 1.
The normalized power in each tone is (√2/4)2 = ⅛. Because the total power is the sum of the power in each tone, the total power is ¼. Therefore, Y(t) exhibits a power loss of 6 dB relative to the maximum possible output power of (1)2 = 1 (the power of a single sinusoid with a peak value of 1).
Note that if the input signals are replaced by sine functions, the results would be the same as those obtained here, except that Y(t) would contain sine functions.
Quadrature Sinusoidal Input Signal Analysis: I(t) = A × cos(ωBt) and Q(t) = B × sin(ωBt)
In this case, the I and Q input signals constitute a quadrature tone (cosine and sine functions, respectively) with a baseband radian frequency of ωB. The I signal is scaled by A (0 ≤ A ≤ 1), and the Q signal is scaled by B (0 ≤ B ≤ 1). Based on Equation 1, Y(t) is expressed as
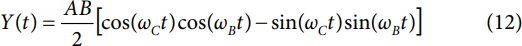
Application of Equation 2 and Equation 3 to the form of Y(t) shown in Equation 12, and then simplifying the equation leads to

Notice that Y(t) contains only a single cosine term, implying that Y(t) consists of a single tone. Its radian frequency is the sum of the baseband radian frequency (ωB) and the carrier radian frequency (ωC) with the amplitude of the tone scaled by ½AB.
It is instructive to consider the case of A = B = 1; that is, the I and Q signals both have peak values that span the full-scale input range. In this case, Y(t) takes the following form:

Note that the peak amplitude of the single tone output is ½. This represents a gain of −6 dB relative to the maximum possible peak output value of 1. The normalized output power is (½)2 = ¼, which represents a power loss of 6 dB relative to the maximum possible output power of (1)2 = 1.
Intrinsic Attenuation
It was shown in the previous sections that an N-bit digital quadrature modulator exhibits an intrinsic attenuation and that the attenuation is dependent on the type of signal applied at the I and Q inputs. The attenuation factors for the three input signal types are summarized in the following list:
- Static: −3 dB
- Nonquadrature tone: −3 dB composite (−9 dB each tone)
- Quadrature tone: −6 dB
The intrinsic attenuation imposed by a digital quadrature modulator can be overcome by including a digital multiplier at the modulator output. The multiplier serves as an amplifier to offset the intrinsic attenuation of the modulator. The amount of amplification that can be tolerated without numeric overflow depends on the amplitude of the I and Q input signals. However, for full-scale I and Q input signals, an upper bound must be imposed on the amplification factor to prevent numeric overflow. When the input signal is a quadraturetone, the amplification factor must be limited to 2.0 (or 6 dB). When the input signal is either a nonquadraturetone or a static value, the amplification factor must be limited to 1.414 (or 3 dB).
Intrinsic Power Loss
The intrinsic attenuation imposed by an N-bit digital quadrature modulator leads to a loss of signal power relative to the power of a full scale, N-bit sinusoidal tone. The degree of power loss is dependent on the type of signal applied at the I and Q inputs. The relative output power for the three input signal types is summarized in the following list:
- Static: −3 dB
- Nonquadrature tone: −6 dB composite (−9 dB each tone)
- Quadrature tone: −6 dB
The power loss related to the different input signal types (see Figure 2) is apparent when the modulator drives a DAC and a spectrum analyzer is connected to the DAC output to measure the signal power. Because the modulator has an N-bit output, the reference power is that of an N-bit quantized sinusoidal tone. The power level of such a tone as measured by the spectrum analyzer is the reference level for the following discussion and is denoted as 0 dBr.

Figure 2. Relative Power Spectrum.
With an N-bit digital modulator driving an N-bit DAC (as shown in Figure 1), the output power is dependent on the type of signal applied at the I and Q inputs. Specifically, when the I and Q inputs of the modulator are driven by a full-scale static input signal, the output of the DAC is a single tone at the carrier frequency (fC) with an output power level of −3 dBr. When the I and Q inputs of the modulator are driven by a full-scale quadraturetone, the output of the DAC is a single tone at a frequency of fC+ fB with an output power level of −6 dBr. When the I and Q inputs of the modulator are driven by a full-scale nonquadrature tone, the output of the DAC consists of two frequencies (fC ± fB) with an output power level of −9 dBr for each tone. The composite signal power (both tones combined) is −6 dBr, which is twice the power in either one of the output tones.
