电源调制比揭秘:PSMR与PSRR有何不同?
摘要
许多雷达系统要求低相位噪声以较大限度抑制杂波。高性能雷达需要特别关注相位噪声,导致在降低频率合成器的相位噪声和表征频率合成器部件的相位噪声方面投入了大量的设计资源。
大家知道,为实现低相位噪声性能,尤其是超低相位噪声性能,必须使用低噪声电源才能达到较佳性能。但文献上没有详细说明如何通过一种系统化方法来量化电源噪声电压电平对相位噪声的影响。本文旨在改变这种状况。
本文提出了电源调制比(PSMR)理论,用来衡量电源缺陷如何被调制到RF载波上。通过电源噪声对RF放大器相位噪声的贡献来验证这一理论;测量结果表明,可以计算并且相当准确地预测该贡献。基于此结果,本文还讨论了描述电源特性的系统化方法。
导言和定义
电源调制比与众所周知的电源抑制比(PSRR)相似,但有一个关键不同点。PSRR衡量电源缺陷直接耦合到器件输出的程度。PSMR衡量电源缺陷(纹波和噪声)如何被调制到RF载波上。
下面的"原理"部分引入了一个将PSMR与电源缺陷相关联的传递函数H(s),用以定量地说明电源缺陷如何被调制到载波上。H(s)具有幅度和相位两个分量,可以随着频率和器件工作条件而变化。尽管变量很多,但一旦确定其特征,便可以利用电源调制比并根据电源数据手册中的纹波和噪声规格来准确预测电源的相位噪声和杂散贡献。
原理
考虑用于RF器件的直流电源上的纹波。电源纹波用一个正弦波信号来模拟,其峰峰值电压以直流输出为中心。该正弦波被调制到RF载波上,在等于正弦波频率的频率偏移处产生杂散信号。
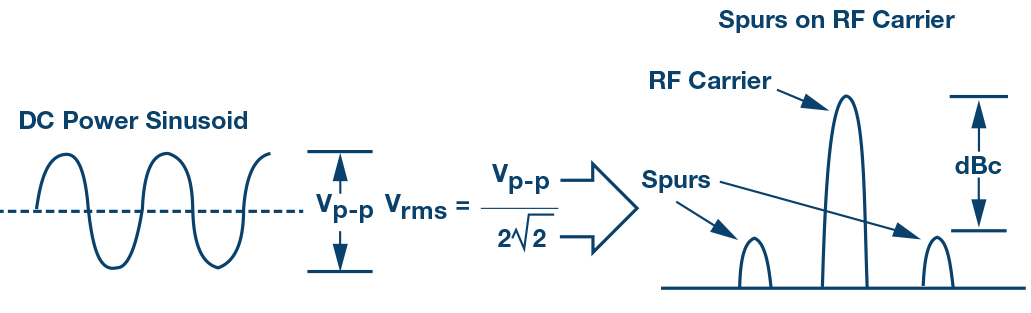
图1. 电源上的正弦波纹波调制到RF载波上产生杂散信号。
杂散水平与正弦波幅度和RF电路灵敏度均有关系。杂散信号可以进一步分解为幅度调制分量和相位调制分量。总杂散功率水平等于幅度调制(AM)分量的杂散功率加上相位调制(PM)分量的杂散功率。
对于这里的讨论,H(s)是从电源缺陷到RF载波上的干扰调制项的传递函数。H(s)同样有AM和PM两个分量。H(s)的AM分量是Hm (s),H(s)的PM分量是HØ (s)。以下等式利用H(s)进行实际RF测量,假设低电平调制可用来模拟电源对RF载波的影响。
信号的幅度调制可以写成
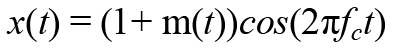
幅度调制分量m(t)可以写成
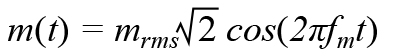
其中fm是调制频率
RF载波的AM调制电平可以直接与电源纹波相关,关系式如下:
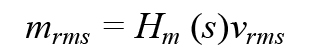
vrms是电源电压的交流分量的均方根值。等式3是关键等式,它提供了一种计算电源纹波引起的RF载波AM调制的机制。
杂散电平可以通过幅度调制来计算
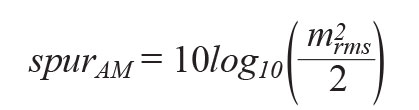
类似地可以写出电源对相位调制的影响。相位调制信号为
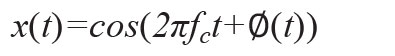
相位调制项为
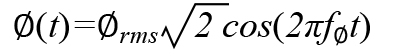
同样,相位调制可以直接与电源相关,关系式如下:
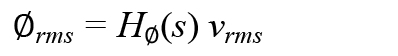
等式7是提供了一种计算电源纹波引起的RF载波PM调制的机制。相位调制引起的杂散电平为
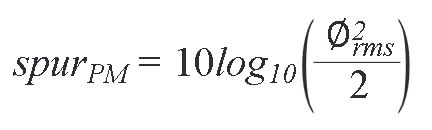
为了帮助可视化mrms和Ørms的杂散影响,图2显示了杂散电平与mrms和Ørms的关系。
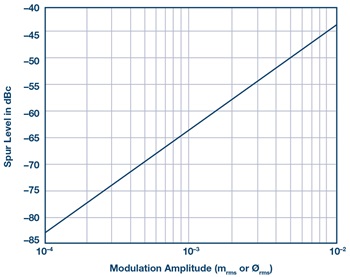
图2. 杂散电平与mrms和Ørms的关系。
总结一下上面的讨论,电源上的纹波转换为电源电压交流项的 均方根电压vrms的调制项mrms和Ørms。Hm (s)和HØ (s)分别是从vrms到mrms和Ørms的传递函数。
现在考虑相位噪声。正如正弦波调制到载波上产生杂散信号一样,1/f电压噪声密度也会调制到载波上产生相位噪声。
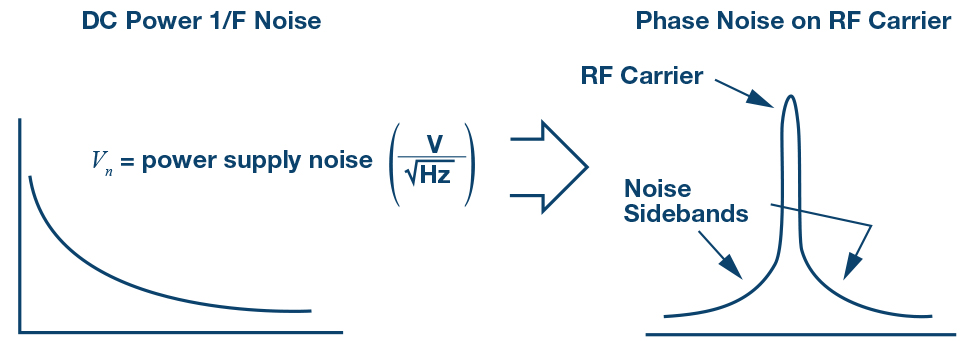
图3. 电源上的1/f噪声调制到RF载波上产生相位噪声。
同样,如果我们考虑一个具有相位调制的信号x(t),那么
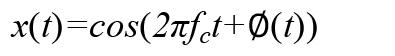
在这种情况下,Ø(t )是一个噪声项。
功率谱密度定义为
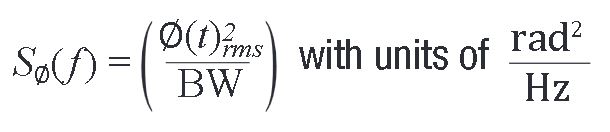
相位噪声依据功率谱密度来定义
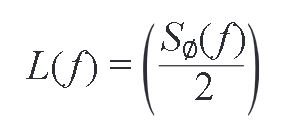
接下来,对于电源纹波引起的相位调制所产生的杂散,将同样的HØ (s)应用于相位噪声。 在这种情况下,HØ (s)用于计算电源上1/f噪声产生的相位噪声。
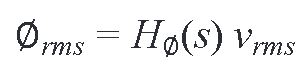
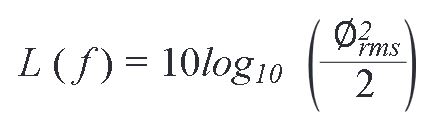
测量实例
为了演示上述原理,我们表征了 HMC589A RF放大器的电源灵敏度和相位噪声,利用多个电源测量了这些量。用于表征的HMC589A评估电路如图4所示。
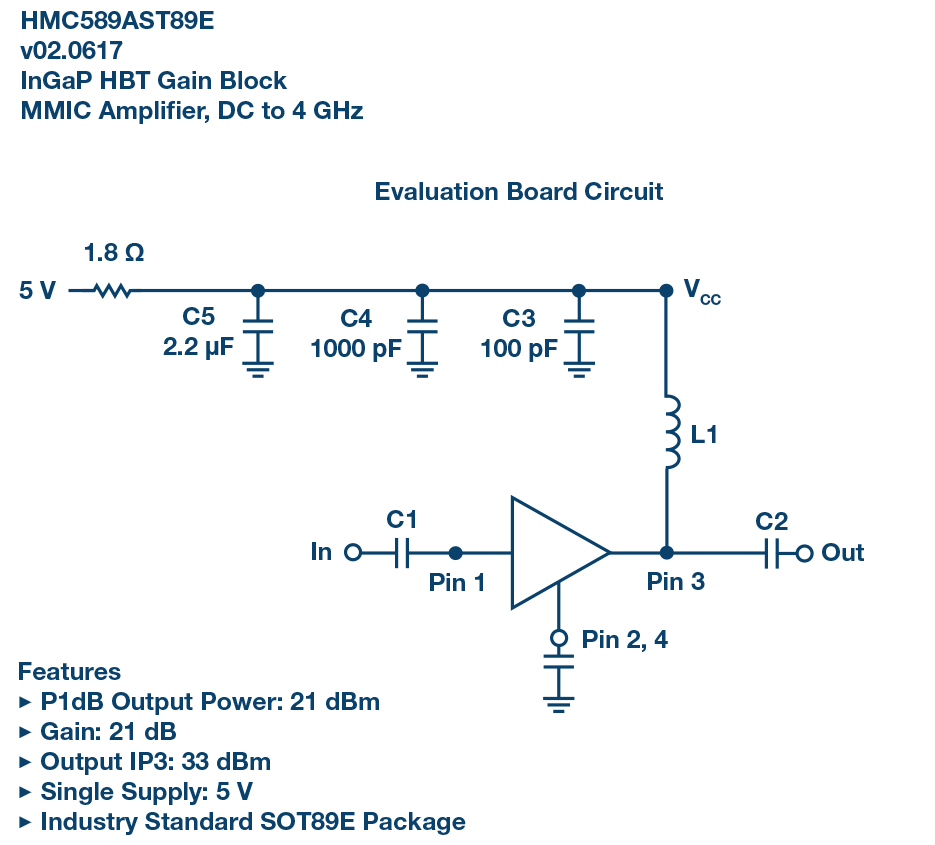
图4. 使用HMC589A放大器来演示PSMR原理。
为了表征电源灵敏度,将一个正弦波注入5 V电源。正弦波在RF上产生杂散信号,以dBc来衡量杂散信号大小。杂散内容进一步分解为AM分量和PM分量。采用Rohde & Schwarz FSWP26相位噪声分析仪和频谱分析仪。AM和PM杂散电平分别通过AM和PM噪声测量来衡量,并使能杂散测量。结果列成表格,测试条件为3.2 GHz,RF输入为0 dBm。
| 输入正弦波 | 实测杂散 | 计算所得H(s) | |||||
| 频率 | V (rms) | 杂散(dBc) | 杂散(dBc) AM | 杂散 (dBc) PM | H (s) | H (s) AM | H (s) PM |
| 100 | 0.01 | –52.2 | –57.3 | –53.7 | 0.35 | 0.19 | 0.29 |
| 1000 | 0.01 | –52.4 | –57.2 | –54 | 0.34 | 0.20 | 0.28 |
| 10000 | 0.01 | –53.5 | –58.3 | –55.3 | 0.30 | 0.17 | 0.24 |
| 50000 | 0.0066 | –61 | –65 | –62.9 | 0.19 | 0.12 | 0.15 |
测试数据表明,RF放大器的电源灵敏度可以利用正弦波调制凭经验测量,结果可用来预测电源噪声对相位噪声的贡献。更一般地,这可以扩展到任何RF器件。这里我们用放大器表征和测量来演示原理。
首先,使用一个噪声相当高的电源。测量噪声密度。基于表征的HØ (s)计算电源对相位噪声的贡献,并与相位噪声测量值进行比较。使用Rhode & Schwarz FSWP26进行测量。噪声电压通过基带噪声测量来衡量。利用测试装置的内部振荡器测量加性相位噪声,以此来衡量放大器残余相位噪声。测试配置如图5所示。在这种配置中,振荡器噪声在混频器中被消除,任何不常见的噪声都会在交互相关算法中予以消除。这样,用户便可实现非常低电平的残余噪声测量。
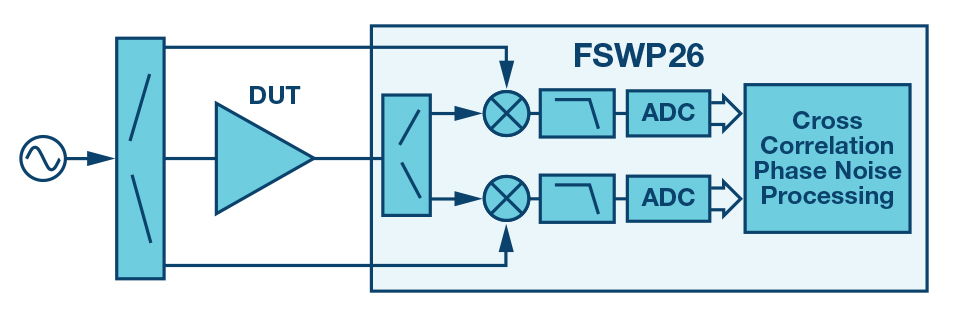
图5. 采用交互相关方法的放大器残余相位噪声测试设置。
电源噪声、实测相位噪声和预测的电源噪声贡献如图6所示。很明显,在100 Hz到100 kHz偏移之间,相位噪声主要由电源决定,关于电源贡献的预测非常准确。
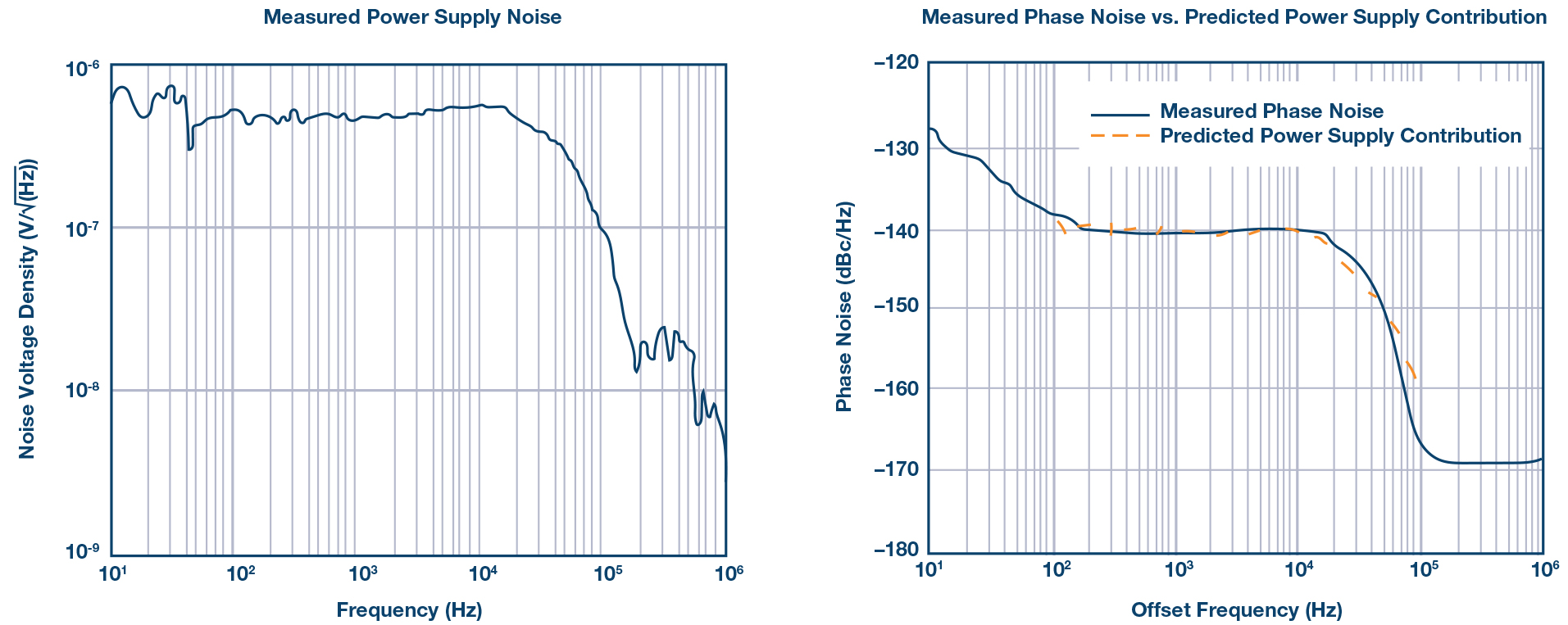
图6. 使用高噪声电源进行技术验证。
用另外两个电源重复该测试。结果如图7所示。同样,电源对相位噪声的贡献是完全可以预测的。
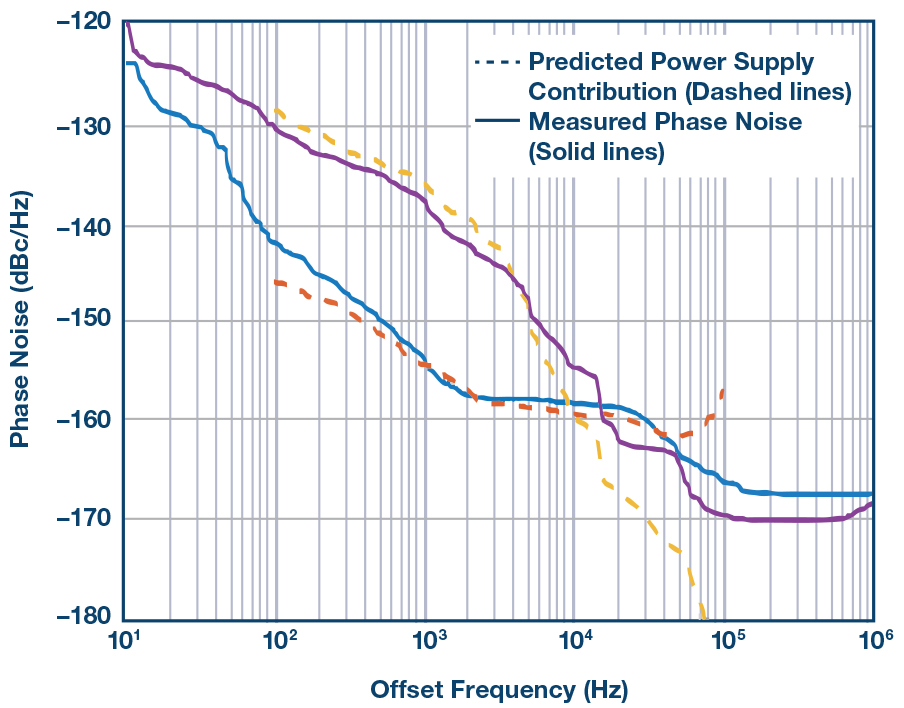
图7. 用另外两个电源验证该技术。
低相位噪声器件表征的一个常见挑战是要确保测量结果属于器件而非周围环境。为了消除测量中的电源贡献,使用 ADM7150 低噪声稳压器。从数据手册中引用的噪声密度以及用于相位噪 声测试的器件的噪声电压测量结果如图8所示。
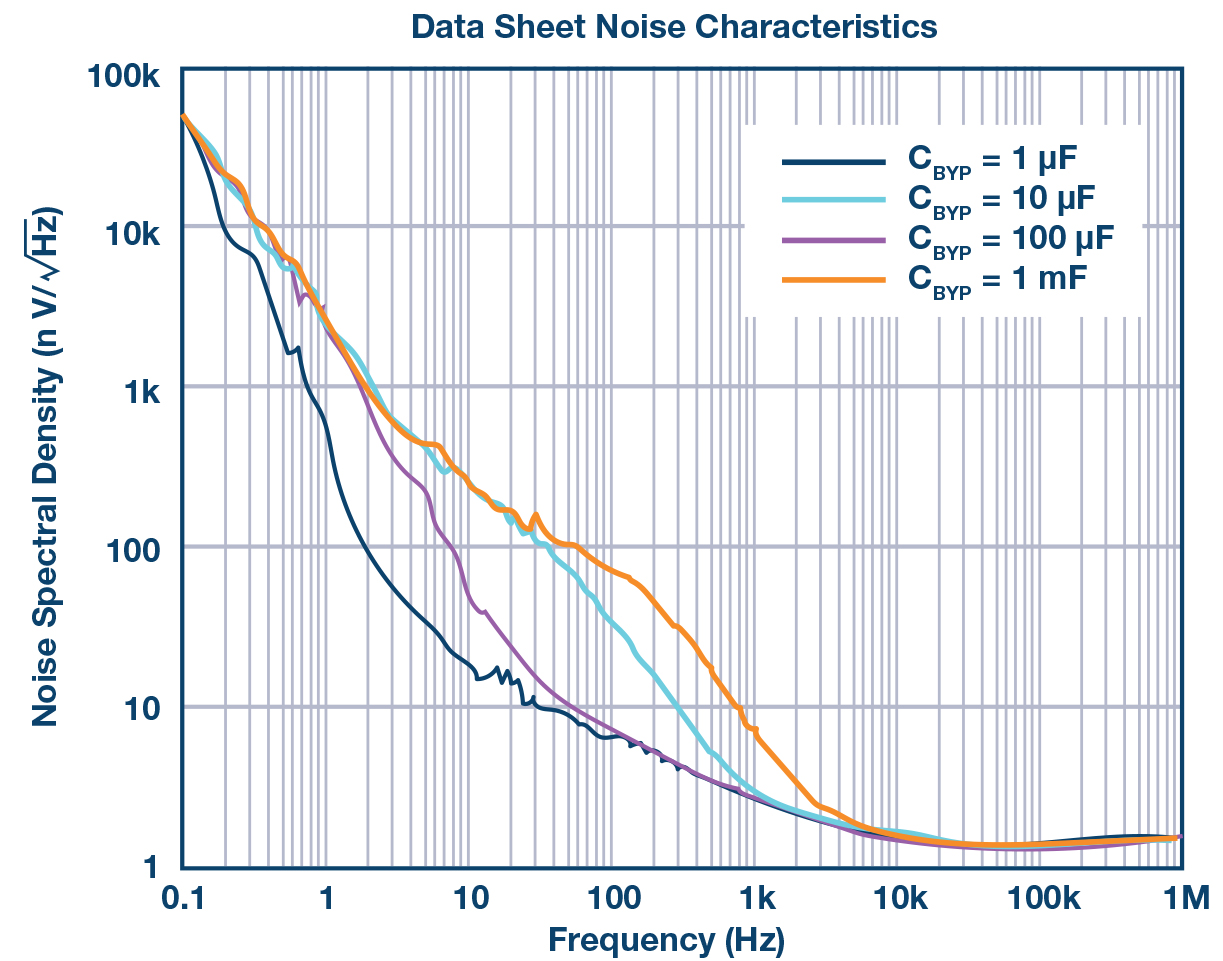
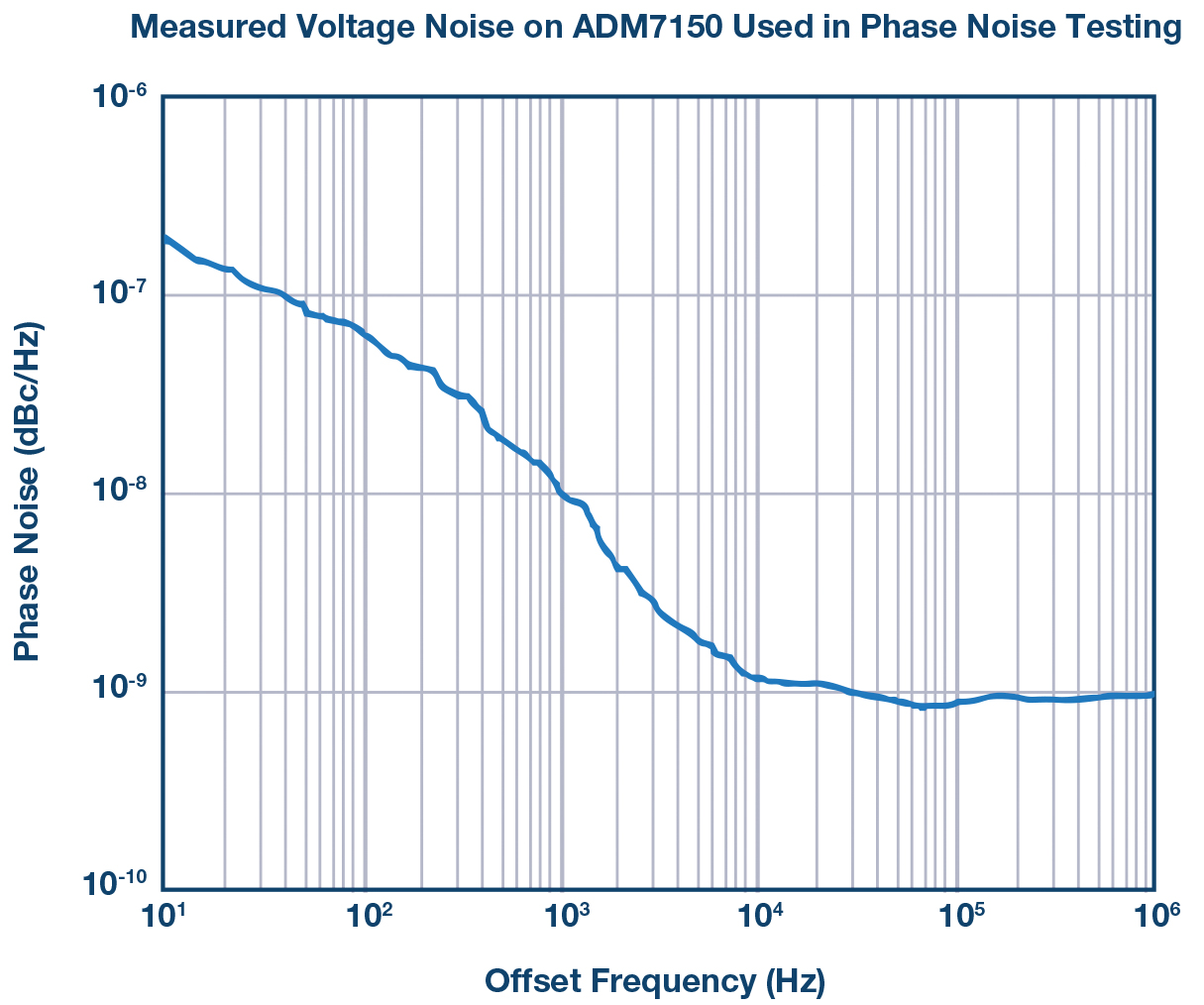
图8. 低噪声稳压器ADM7150的噪声电压密度。
表2列出了一系列低噪声稳压器及其关键参数。这里给出的器件都非常适合为低相位噪声RF设计中的RF器件供电;相关条件和特性曲线请参阅数据手册。数据手册中包括了多个偏移频率下的噪声密度和PSRR曲线。表中显示了10 kHz偏移的噪声密度,因为该区域对许多稳压器而言通常存在限制。所示的PSRR对应于1 MHz偏移,因为许多线性稳压器在这些偏移处会失去抑制能力,需要额外的滤波。
| 产品型号 | VIN 范围 | VOUT 范围 | IOUT | 固定/ 可调节 | 噪声密度(10 kHz) | PSSR @ 1 MHz |
| LT3042 | 1.8 V 至 20 V | 0 V 至 15 V | 200 mA | 可调 | 2 nV/√Hz | 79 dB |
| LT3045, LT3045-1 | 1.8 V 至 20 V | 0 V 至 15 V | 500 mA | 可调 | 2 nV/√Hz | 76 dB |
| ADM7154 | 2.3 V 至 5.5 V | 1.2 V 至 3.3 V | 600 mA | 固定 | 1.5 nV/√Hz | 58 dB |
| ADM7155 | 2.3 V 至 5.5 V | 1.2 V 至 3.4 V | 600 mA | 可调 | 1.5 nV/√Hz | 57 dB |
| ADM7150 | 4.5 V 至 16 V | 1.8 V 至 5 V | 800 mA | 固定 | 1.7 nV/√Hz | >60 dB |
| ADP7156 | 2.3 V 至 5.5 V | 1.2 V 至 3.3 V | 1.2 A | 固定 | 1.7 nV/√Hz | 60 dB |
| ADP7157 | 2.3 V 至 5.5 V | 1.2 V 至 3.3 V | 1.2 A | 可调 | 1.7 nV/√Hz | 55 dB |
| ADP7158 | 2.3 V 至 5.5 V | 1.2 V 至 3.3 V | 2 A | 固定 | 1.7 nV/√Hz | 50 dB |
| ADP7159 | 2.3 V 至 5.5 V | 1.2 V 至 3.3 V | 2 A | 可调 | 1.7 nV/√Hz | 45 dB |
从ADM7150供电时,HMC589A残余相位噪声测试的结果如图9所示。该测量结果显示了放大器的真实性能,其本底噪声低于-170 dBc / Hz,并且此性能一直保持到10 kHz偏移。
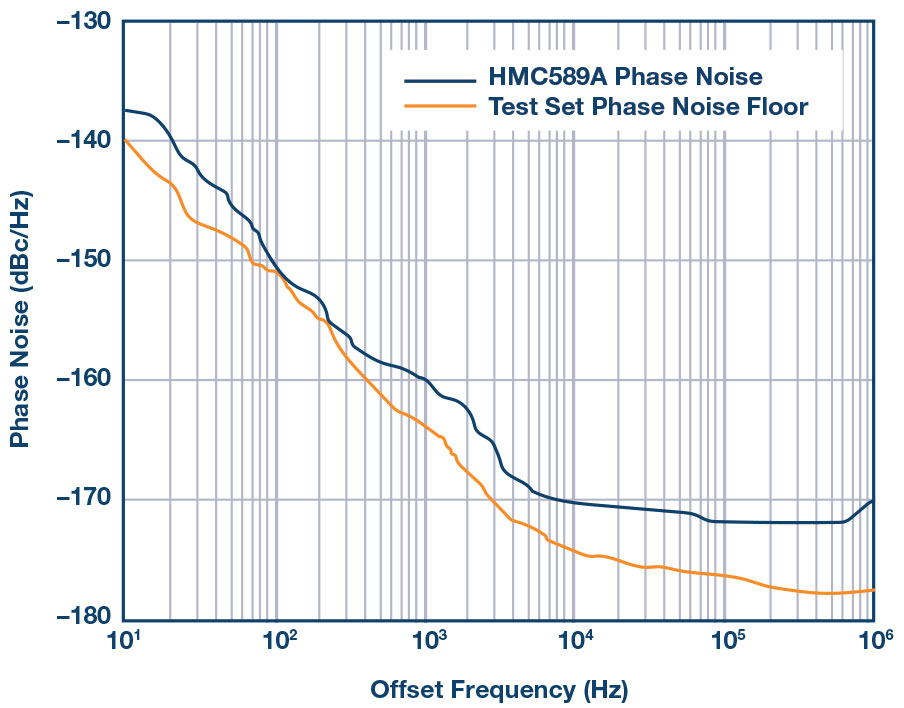
图9. HMC589A残余相位噪声,3.2 GHz,输入RF功率为0 dBm,ADM7150稳压器提供直流电源。
描述电源特性的系统化方法
低相位噪声应用的电源设计通常会不加考虑地选择可用的较佳稳压方案,而无视实际较低规格,这会导致过度设计。对于小批量设计,这种方法可能值得继续,但对于大批量生产,性能、成本和复杂性必须优化,过度设计可能是一种不受欢迎的浪费。
下面是一种定量推导电源规格的方法:
- 用正弦波调制电源以表征H(s)。H(s)将是频率的函数,每十倍频程测试一次。
- 分配电源对杂散和相位噪声的贡献,在RF规格之下留一定的裕量。
- 计算电源纹波规格,
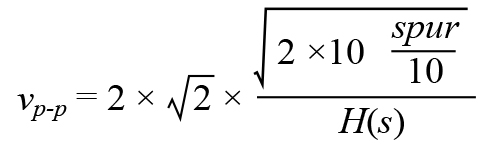
- 计算电源噪声规格,

上述第一步中的一个重要事项是了解Hm (s)和HØ (s)在设计预期的工作条件下如何变化。在HMC589A表征中,此变化是在若干功率水平下进行测量,如图10所示。
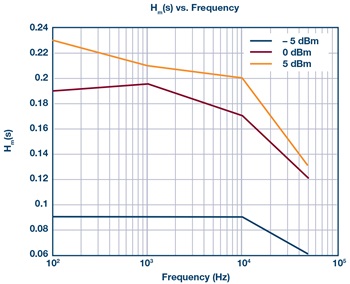
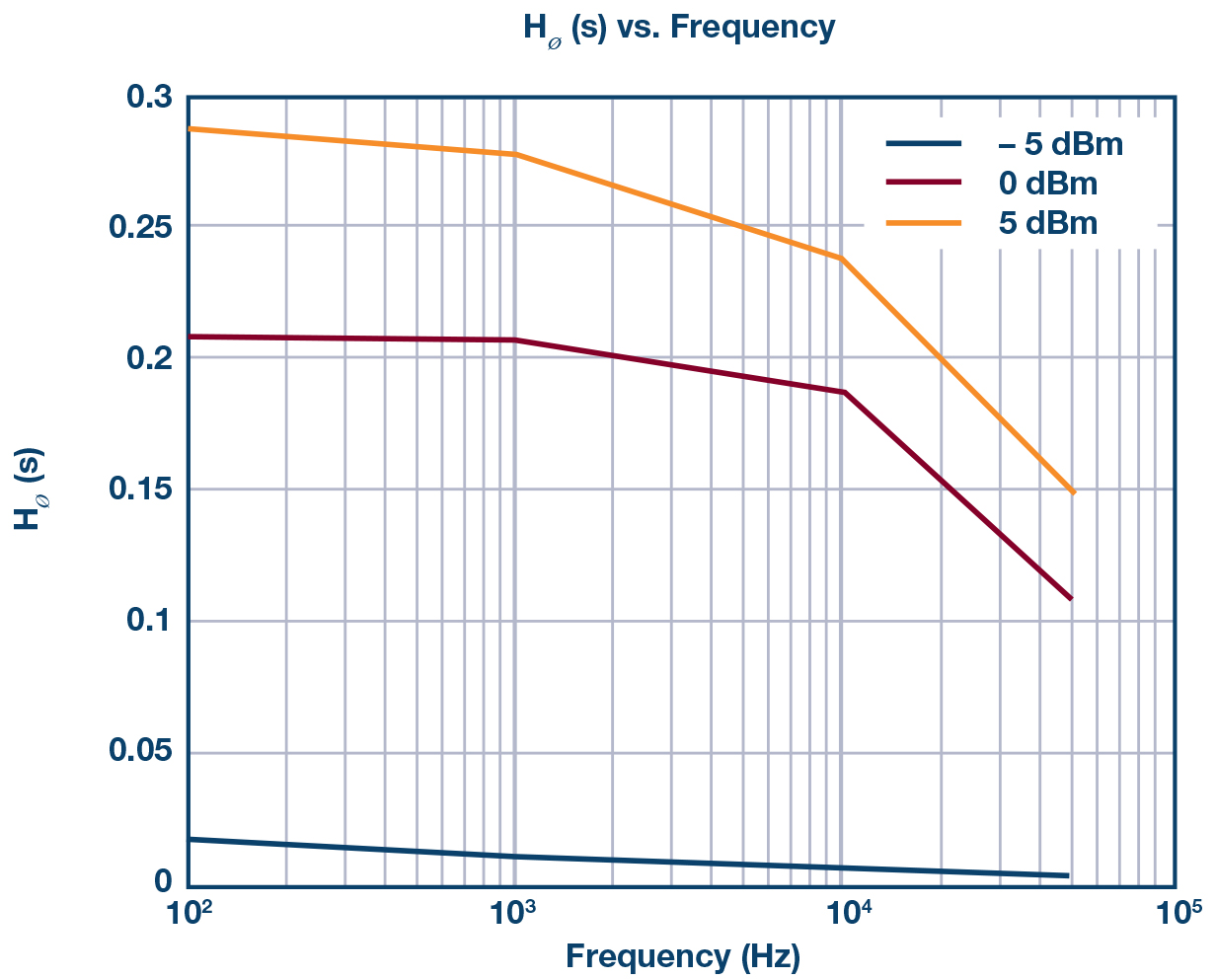
图10. Hm (s)和HØ (s)的变化与偏移频率和功率水平的关系,使用HMC589A评估电路,频率为3.2 GHz。
结语
虽然人们普遍认为,在RF应用中应限制电源纹波和噪声,但很少有人充分理解其定量影响。利用本文所述的系统化方法,工程师可以按部就班地量化电源对期望RF性能的影响,从而做出明智的电源选择。




















