要約

このアプリケーションノートでは、RTD温度測定の誤差を最小化する方法を説明します。

はじめに

高精度温度測定は、産業オートメーションアプリケーションが製品の品質と安全性の両方を確保するため不可欠なデータを提供します。多数のタイプの温度センサーが利用可能で、それぞれに利点と欠点があります。このアプリケーションノートでは測温抵抗体(RTD)に焦点を当て、測定精度を最適化するための設計の基礎を説明します。

測温抵抗体

RTDは、温度で抵抗値が変化する素子を内蔵しています。ほとんどの素子は、白金、ニッケル、または銅のいずれかです。白金RTDは、広い温度範囲にわたって最も直線性と再現性の高い温度-抵抗値の関係を備えているため、最高の性能を提供します。

一般に、RTDは熱電対やサーミスタに比べて、より安定性と再現性の高い出力を生成します。そのため、RTDはより高い測定精度を実現します。

高精度RTD測定の設計オプション

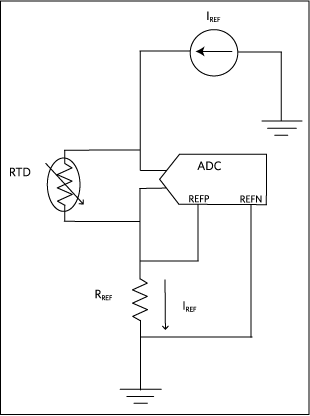
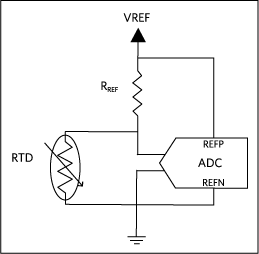
RTDを測定するための2つの最も一般的な方法は、定電流励起(図1)と定電圧励起(図2)です。

目的は、RTDの抵抗値を高精度で測定し、式またはルックアップテーブルを使用して温度に変換することです。理想的な場合は、以下のようになります。

(定電流励起の場合)

または

(定電圧励起の場合)

しかし実際には、RTDのリードワイヤには抵抗があります。長いリードワイヤは、測定精度に大きく影響します。そのため、図1および2に示す回路によって測定される実際の抵抗値は、次のようになります。

RTD + (2 × R_WIRE)

ここで、R_WIREはリードワイヤの抵抗で、両方のワイヤが同一の抵抗値を備えていると仮定しています。理論的には許容可能ですが、R_WIREが同じということは、両方のワイヤが完全に同じ長さで、完全に同じ材質でできていることを意味します。そのような仮定は、重要な温度検出アプリケーションでは保証することができません。そのため、RTDはリードワイヤに起因する測定誤差の除去に役立つよう、3線式または4線式の構成を備えています。

3線式RTD構成

3線式RTD用の標準的な定電流および定電圧励起回路を、それぞれ図3および図4に示します。どちらの場合も、ADCはRTDの抵抗値 + R_WIRE3 (R_WIRE3はリターンリードワイヤの抵抗値)をサンプリングします。ADCの入力は通常はハイインピーダンスで、R_WIRE2を流れる電流は事実上ゼロになるため、このシステムはR_WIRE2を除去しています。したがって、ADCはRTDおよびR_WIRE3両端の電圧のみを測定します。R_WIRE3は測定誤差に寄与します。しかし、2線式構成と比較するとリードワイヤに起因する誤差はおよそ50%減少します。

測定精度をさらに向上させる方法の1つは、回路にアナログスイッチを追加することです。その場合、ADCは励起信号の出力の電圧(V_X)を測定し、R_WIRE1の値を取得します。R_WIRE1がほぼR_WIRE3と同じだと仮定することによって、R_WIRE3を除去することができます。図3を参照すると、電流励起構成において、R_WIRE1の抵抗値は次式に等しくなります。

そして、向上したRTD測定の近似値は、次のとおりです。

電圧励起構成の場合は、以下のようになります。

および、

この方式による測定精度の向上は、追加のハードウェアが必要であり、ソフトウェアの複雑性も増大します。

4線式RTD構成

4線式RTD構成は、最高の測定精度を提供します。 図5および図6は、それぞれ4線式RTDの定電流励起および定電圧励起回路を示します。電流励起構成の場合、R_WIRE2またはR_WIRE3を通る電流はないため、次のようになります。

したがって、R_WIRE2 + RTD + R_WIRE3両端の電圧は、RTD両端の電圧と同一になります。残念なことに、定電圧励起構成を使用する場合、ADCシステムが励起電圧出力の電圧(V_X)を測定することができない限り、抵抗分圧器の作用によって、R_WIRE1およびR_WIRE4がやはりRTD測定の誤差を生じさせます。V_Xの電圧が既知の場合は、次式によってリファレンス電流を計算することができます。

ここで、R_REFはこの場合は3.32kΩです。同様に、次式は電流励起構成の場合の式と同一になります。

信号チェーン内のその他の多数の要素が、測定精度に影響します。これらの要素には、ADCシステムの入力インピーダンス、ADCの分解能、RTDを流れる電流の量、電圧リファレンスの安定性、および励起信号の安定性が含まれます。

リードワイヤ両端(たとえば4線式構成のR_WIRE2およびR_WIRE3)での電圧降下を防ぐために、ADCシステムの入力はハイインピーダンスである必要があります。ADCがハイインピーダンス入力を備えていない場合は、ADCの入力の前にバッファを追加してください。

加熱誤差

RTDはセンサーですが、抵抗でもあります。電流が抵抗を通って流れると、消費電力が発生します。消費電力は、抵抗を加熱します。この自己加熱効果によって、測定に誤差が生じます。励起電流を注意深く選択して、発生する誤差がエラーバジェット内に収まることを確保する必要があります。自己加熱誤差の主要な計算式は、次のとおりです。

ΔT = (I²_REF ×R_RTD) × F

ここで、FはRTDの自己加熱係数で、mW/℃で表されます。たとえば、自己加熱係数が0.05℃/mWのPT-100白金RTDを氷水に入れます。測定温度が0℃のとき、R_RTDは100Ωです。I_REFを10mAに設定した場合、自己加熱誤差は次のようになります。

((0.01A)² × 100Ω) × 50°C/W = 0.5°C

アプリケーションによって、この誤差を許容することができる場合とできない場合があります。高精度測定の場合、より低い励起電流を使うと自己加熱誤差が低減します。たとえば、I_REFを1mAに低めると、自己加熱誤差は0.005℃になります。このレベルの誤差なら、はるかに許容可能です。励起電流を下げると自己加熱誤差が低減しますが、RTD両端での電圧信号の範囲も狭まるため、ADCがより多くの分離した信号レベルを抽出することができるように、RTD信号を増幅する必要が生じます。別の方法としては、より高分解能のADCを使用することが考えられます。

ここまでの段階で、解説してきたすべての式にI_REFまたはV_REFのいずれかが含まれていました。しかし、これらの励起信号が安定性を欠く場合はどうなるでしょう？不安定性は、短期的または長期的ドリフトによって生じます。明らかに、励起信号が不正確になると、上記のすべての計算に誤差が含まれることになります。そのため、定期的な較正が必要です。もちろん、エンジニアは超低温度ドリフト/長期的ドリフトを備えた非常に安定性の高い電圧リファレンスを使用することもできます。しかし、通常そのようなデバイスは非常に高コストです。別の方法として、レシオメトリック温度測定法は、不正確な励起信号に起因する誤差を除去します。

レシオメトリック温度測定

レシオメトリック測定は、絶対電圧を使用して抵抗を測定する代わりに、リファレンス抵抗に対する比としてRTDの抵抗値の測定を提供します。言い換えると、R_RTDはV_REFまたはI_REFではなくR_REFの関数になります。この方法では、同じ励起信号を使用して、RTD両端の電圧とADC用の電圧リファレンスの両方を生成します。励起信号が変化すると、その変化はRTD両端の電圧とADCのリファレンス入力の両方に反映されます。 図7および図8は、電流励起構成と電圧励起構成のレシオメトリック測定回路を示します。

一般的なADCの変換公式は、次のとおりです。

ここで、

V_IN = ADCの入力電圧
V_REF = リファレンス電圧(REFP - REFN)
CODE = ADCコード
N = ADCの分解能

V_INはRTD両端の電圧と等しい値です。電流励起モードの場合、以下のようになります。

V_IN = I_REF × R_RTDおよびV_REF = I_REF × R_REF。

V_INおよびV_REFをADCの変換公式に代入すると、次式を得ます。

そこから次式を得ます。

同様に、電圧励起の場合は次のようになります。

V_INをADCの変換公式に代入すると、次式を得ます。

R_RTDについて解くと、次式を得ます。

どちらの場合も、式の簡約化のあと、R_RTDはR_REFとADCコードの関数になります。したがって、RTD測定の精度はR_REFに依存します。そのため、リファレンス抵抗を選択するときに、エンジニアは低い温度ドリフト/長期的ドリフトを備えたものを選ぶ必要があります。

RTDから温度への変換

回路がどれほど正確にRTDの抵抗値を測定しても、エンジニアが適切な方法を使って高精度でRTDの抵抗値を温度に変換しなければ、すべての努力は無駄になります。一般的な方法の1つは、ルックアップテーブルの使用です。しかし、要求される分解能が高く、測定対象の温度範囲が広い場合、ルックアップテーブルが肥大化し、この方法の有効性が低下します。もう1つの方法は、温度を計算することです。

白金RTDの場合、抵抗値と温度の関係はCallendar-Van Dusenの式によって次のように表されます。

R(t) = R0 × (1 + A × t +B × t² + (t - 100) × C × t³)

ここで、

R(t) = RTDの抵抗値
t = 温度
R0 = 0℃でのRTDの抵抗値
A = 3.908 × 10^-3
B = -5.775 × 10^-7
C = -4.183 × 10^-12 (t < 0℃の場合)
C = 0 (t > 0℃の場合)

この式は、既知の温度を与えると、予想されるRTDの抵抗値を提供します。対象の温度範囲が0℃以上の場合、定数Cは0になり、式は2次式になります。2次式を解くのは簡単です。しかし、温度が0℃を下回り、定数Cが0ではなくなると、式は難解な4次式になります。この場合、多項式補間による近似が非常に有効なツールとなります。Microsoft Excelのソリューションの例を示します。

1. スプレッドシート上に、2列のデータを作成します。1つの列に、温度を記入します。第2の列に、Callendar-Van Dusenの式から計算した対応するRTD抵抗値を記入します。
2. X-Y散布図を作成します。
3. グラフに多項式近似曲線を追加します。多項式が高次であるほど、より高精度の近似が得られます。
4. ｢近似曲線の書式設定｣メニューで、｢グラフに数式を表示する｣を選択します。

PT100でt < 0℃の場合、結果の多項式は次のようになります。

t = -1.6030e -13 × r⁶ + 2.0936e -10 × r⁵ -3.6239e -8 × r⁴ -4.2504e -6 × r³ + 2.5646e -3 × r² + 2.2233 × r -2.4204e2

多項式係数の小数点以下の桁数を増やすと、誤差が減少します。上記の式のように小数点以下4桁の場合、温度近似誤差は0.005℃以下になり、ほとんどのアプリケーションにとって許容可能となります。

マキシムのリファレンスデザインソリューション

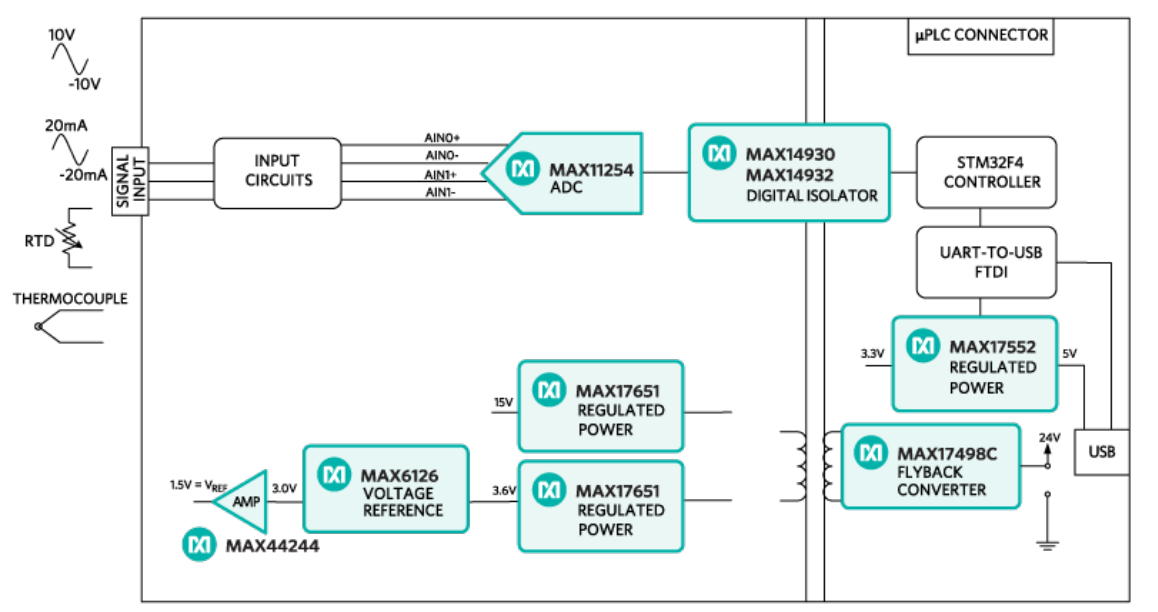
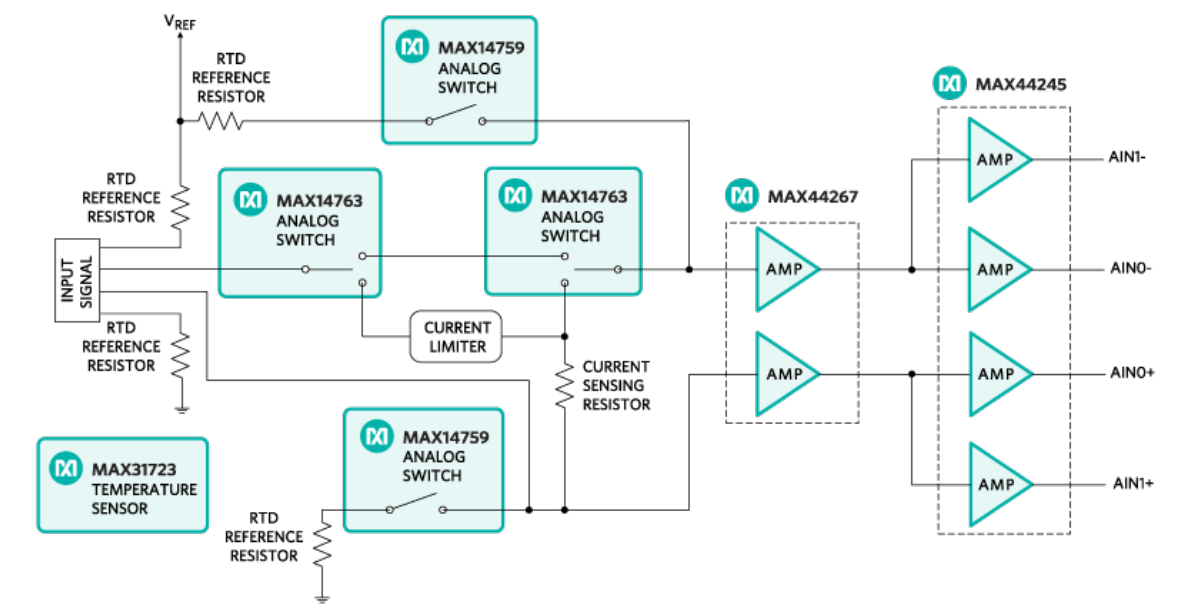
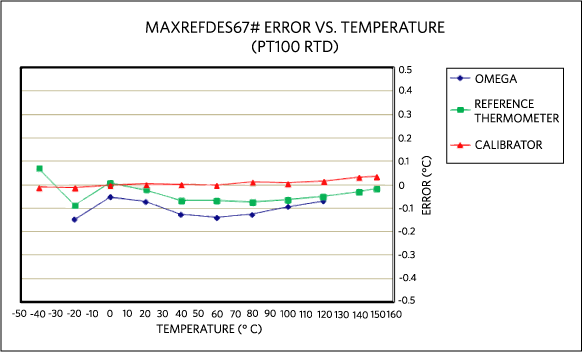
MAXREFDES67#リファレンスデザインは、上記の4線式レシオメトリック構成および多項式近似を実装しています。また、後から変更および実装が可能なように、設計ファイルとファームウェアが利用可能です。さらに、このリファレンスデザイン(図9、10、11)は、産業アプリケーション用の完全な汎用アナログ入力です。この独自の24ビットフロントエンドは、RTD測定以外にもバイポーラ電圧および電流、および熱電対(TC)入力を受け付けます。MAXREFDES67#はマキシムの超小型Micro PLC形状に実装され、最大22.3ビットの実効分解能で動作し、温度誤差は-40℃～150℃の範囲にわたってわずか±0.1%です。図12は、MAXREFDES67#のRTD入力によって測定された温度誤差と、3種類の温度計を基準とする温度との関係を示します。基準は、それぞれOmega HH41温度計、ETIリファレンス温度計、およびFluke 724温度キャリブレータです。MAXREFDES67#に接続したRTDプローブ(Omega P-M-1/10-1/4-6-0-G-3)をFluke 7341較正用バスに入れ、20℃で較正を行いました。

結論

温度は、最も多く測定される産業パラメータです。レシオメトリック法や多項式近似などの手法を使用した高精度システム設計によって非常に高精度の測定システムを実現することが可能ですが、マキシムのリファレンスデザインシステムを使うと、設計者はこれまで以上に迅速に高精度RTD温度測定または熱電対測定システムを開発することができます。MAXREFDES67#は変更および実装が可能で、産業アプリケーション用の完全な汎用アナログ入力です。RTD測定以外に、バイポーラ電圧、電流、および熱電対入力を受け付け、実効分解能で動作し、低測定誤差によって他のオプションより高い能力を発揮します。

このアプリケーションノートは、2016年2月にEDN Networkに掲載されました。