要約

IP3（Third-order Intercept Point：3次インターセプト・ポイント）は、RF対応の機能／コンポーネントの直線性を評価するために使用される指標です。本稿では、基本的な数式とグラフを使用することで、IP3がどのように発生し、その値がデバイスの入力電力や出力電力などにどのような影響を及ぼすのかを明らかにします。RF対応の機能やコンポーネントの性能が優れていると判断するためには、IP3が高い（つまり直線性が高い）ことが非常に重要になります。本稿では、その理由についても解説します。更に、IP3の高さが性能の証となる高性能のアナログICを紹介します。

なお、本稿と同様の記事がEDNの2012年6月29日号に掲載されています。

はじめに

本稿では、IP（インターセプト・ポイント）の定義や発生原理、評価方法などについて説明します。IPについては、2から始まる整数nを使用したIPnという表現によって説明されます。これはn次のIPという意味になります。IPnは、ロー・ノイズ・アンプ（LNA）、RFミキサー、パワー・アンプ（PA）といった電子デバイスの直線性を示す指標として用いられます。

IPnは、仮想のパラメータによって構成されています。つまり、実際にはその値は他の指標によって決まるということです。そのため、IPnの値と外挿方法（後述）には曖昧さが存在するケースが少なくありません。RFに関する書籍やチュートリアルを見ると、IPnと入出力電力、パワー・ゲイン、圧縮ポイントの関係について説明されているケースが少なくありません。しかし、それらの資料では、IPnの定義や発生原理については明確に説明されていないことがほとんどです。

現在、LNA、ミキサー、VCO（Voltage Controlled Oscillator）などの機能は、高度な設計手法とシリコン・ゲルマニューム（SiGe）技術などを用いた実績のあるRF向けのプロセスによって実現されています。それにより、最高の直線性（優れたIP3）が得られるようになっています。そうしたデバイスの設計においては、消費電流（バイアス回路の電流）、ゲイン、サイズを犠牲にすることなく、最高のIP3を実現することが目標になります。その際には、5次まで、場合によっては7次までのIPnについて明らかにする（数式で表すなど）ことが重要になります。ただ、高感度のデバイスの通常の性能については、IP3を用いて表現する方法が主流になっています。 

本稿では、基本的な数式とグラフを使用して、IPn、特にIP3がどのように発生し、その値がデバイスの入力電力や出力電力などにどのような影響を及ぼすのかを明らかにします。また、機能やデバイスの性能について判断する上で、なぜIP3が高い（直線性が高い）ことが非常に重要となるのか、その理由について解説します。更に、性能の高さを表現するための指標として直線性（IP3）が使用されているアナログICの具体例を紹介します。 

なぜ直線性が重要なのか？

多くの電子デバイスには、理想的な数学的関数を単純かつ容易に再現することが求められます。最も簡単な例としては抵抗が挙げられます。抵抗製品は、電圧と電流（V-I）の間で直線的な関係が得られるように設計されます。つまり、抵抗は単にV-I特性の傾きを表すものであることが理想です。 

しかし、V = R×Iという理想的な関係を完全に実現するのは不可能だということは周知の事実です。もちろん、理想に近づけることは可能ですが、現実のデバイスに内在する不完全性と限界によって理想的な直線に対する偏差が生じます。そうした偏差は、特に信号（I、V）が大きい場合や、温度、湿度、圧力といった他の条件が変化する場合に発生します。そのような偏差が生じないようにするためには、可能な限り線形な性質を備える抵抗Rを実現しなければなりません。つまり、信号や広範な条件にわたって直線性を維持できるものを実現する必要があります。とはいえ、現実の抵抗では、V-I特性を表す曲線は複雑なものになってしまうのです（図1）。

直線性が適切に制御されている必要があるものは抵抗だけではありません。例えば、アンプ、データ・コンバータ（A/DコンバータとD/Aコンバータ）、VCO、ミキサー、PAといったICも直線性が優れている必要があります。これらのICで、理想的なV-I特性からの偏差が発生すると、不安定な動作、仕様の未達、干渉の発生といった問題が生じます。場合によっては、誤動作が発生したり、デバイスやシステム全体に損傷が及んだりする可能性もあります。

直線性の測定方法

デバイスの直線性を測定するためには、どのような手法を用いればよいのでしょうか。これについては、信号のクラスとダイナミック・レンジについて考慮する必要があります。それらに応じ、現実のデバイスの線形性能を測定、視覚化、評価、比較できるようにしなければなりません。それに向けて、様々なパラメータや手法が定義されています。 

通常、抵抗の直線性は、デバイスの公称値に対する偏差を%（パーセント）単位で測定します。それにより、デバイスの電流や電圧に生じる誤差を十分に評価することができます。 

では、LNA、ミキサー、フィルタ、PAといったRFコンポーネントの性能についてはどう考えればよいのでしょうか。これらのコンポーネントを使用する場合、非常に大きな信号の動きが発生します。その場合、非直線性に重大な影響を及ぼす要因である高調波、干渉、飽和が生じる可能性があります。その結果、入出力の間に非理想的な関係が生じます。その関係を特徴づけるために、以下のようないくつかのパラメータが使用されています。 

• 1dB圧縮ポイント（CP_-1dB）
• 圧縮ダイナミック・レンジ（CDR：Compression Dynamic Range）
• スプリアスフリー・ダイナミック・レンジ（SFDR）
• 減感ダイナミック・レンジ（DDR：Desensitization Dynamic Range）
• n次のIP（IPn）

上記の指標は、いずれもデバイスの直線性の優劣を表します。ただ、これらは独立したものではなく、互いに関連性を持ちます。本稿では、上記の各パラメータを考慮に入れつつも、IPnのnが2、3、4といった値になる場合に焦点を絞ることにします。対象とする信号に対し、非直線性はどのように悪影響を及ぼすのでしょうか。これについては、IPn（特にIP3）を使うことでほぼ明らかになります。IP3が低い場合、対象とする信号帯域に干渉が直接注入されることになります。このことが、他のパラメータに注目することなく、IP3だけに焦点を絞るべき理由になります。端的に言えば、IPnが高くなるほど、デバイスの直線性は高くなるということです。

直線性が低いことに起因する高調波と相互変調

ここでは、一般的な電子回路の機能について考えます。入力電力と出力電力は、それぞれ信号xとyで表されるとします。そして、それらの間の伝達関数をAで表します。例えば、対象とするデバイスがアンプである場合、Aはゲインに相当します。ここで、図1の抵抗の説明について振り返ってみましょう。抵抗に限らず、現実のすべてのデバイスの特性は、「yがxに比例する」ことを表すきれいな直線にはなりません。つまり、それぞれの特性は曲線で表されます。しかも、それ自体も単純な曲線とはならず、信号が大きくなると歪みが現れます。 

x、yの値が小さい場合、その特性は直線に近い曲線になります。設計者がそのことに気づくかどうかに関わらず、非直線性が存在している状態になります。それに対し、xとyが大きい場合には非直線性が非常に目立つ状態になります。その背景には、飽和という現象があります。一般に、デバイスに入力する信号が大きくなっていくと、その出力はいずれ適切な応答を示さなくなります。この現象については、-1dB圧縮ポイントを使用することでうまく説明できます。-1dB圧縮ポイントは、印加できる信号の上限（つまりダイナミック・レンジ）を表す指標です（図2）。

一般に、入力と出力の関係は次の式で表すことができます。 

y = A₀ + A₁.x¹ + A₂.x² + A₃.x³ +... + A_i.xⁱ +... A_n.xⁿ

これは、任意の伝達関数Aをテイラー級数展開したものです。 

純粋な1次関数では、1より大きいすべてのiに対してA_i = 0が成り立つはずです。つまり、1次関数は次式で表されます。

y(Linear) = A₀ + A₁.x

繰り返しになりますが、現実のデバイスではこの式は成り立ちません。つまり、x²、x³、x⁴といった項も存在します。それらの大きさはA₂、A₃、A₄などの係数によって決まります。これらの係数は、伝達関数Aが望ましい比例則から外れる原因だと言えます。

ここで、x(t)が正弦波信号で表されると仮定しましょう。この場合、x(t)には周波数がωの信号成分が1つだけが含まれています。つまり、非常に一般的な正弦波の形で表すとx(t)は次のようになります。 

X(t) = A cos(ω.t + Φ)

オイラーの公式を用いてx(t)を表すと、X(t) = A/2[e^{+j(ωt + Φ)} + e^{-j(ωt + Φ)}]となります。つまり2つの複素数の和として表現できます。以下では、この和の第1項だけに注目することにします（このように式の扱いを簡素化することにより、指数関数の効果だけに注目して説明を進めることができます）。 

ここで、上記のX(t)の式の第1項を次式のように書くことにします。 

x = K e^{j(ωt + Φ)}

デバイス（A）が本当に線形なものであれば、その応答yはxに比例する形になります。つまり、次のような式が成り立ちます。 

y = A₀ + A₁.x

y = A₀ + A₁. K e^{j(ωt + Φ)}

xと同じく、yには1つ周波数成分（ω）だけが含まれることがわかります。このことから重要な結論を導き出すことができます。それは、完全に線形な関数（デバイス）自体が他の周波数成分を生成することはないというものです。 

また、ここで、以下に示す2つの重要な見解についてまとめておきます。 

1. xに、周波数ω_aとω_bに対応する2つの成分が含まれている場合
   デバイスの特性が線形であるなら、上記の仮定は問題にはなりません。その場合、以下の式に示すように、yでは2つの周波数ω_aとω_bが正確に再現されます。

y = A₀ + A₁. (K_ae^{j(ω_at + Φ_a)} + K_be^{j(ω_bt + Φ_b)})

ご覧のとおり、他の周波数成分は発生しません。

2. xに、周波数ω_a、ω_b、ω_c、ω_d、ω_nに対応する複数の成分が含まれている場合
   この場合も、デバイスの特性が線形であるなら、yにはxの歪み成分は生じず、良好な形のままです。つまり、xと同じ周波数成分（それ以上の周波数の成分も、それ以下の周波数の成分も存在しない）がyにも現れます。

非線形のデバイスでは何が起きるのか？

ここでは、xに周波数ωに対応する1つの成分だけが含まれている場合について分析することにしましょう。xとyの関係は以下の式で表されます。

y = A₀ + A₁.x¹ + A₂.x² + A₃.x³ +... + A_i.xⁱ +... A_n.xⁿ

また、以下の式が成り立ちます。

x = K e^{j(ωt + Φ)}

数学的には、(e^m)ⁿ = e^mnが成り立つことに注意してください。

すると、以下のような形で式を分析することができます。

y = A₀ +

A_1. K e^{j(ωt + Φ)} +

（ωが含まれている）

A_2. (K e^{j(ωt + Φ)})² +

（2ωが含まれている）

A_3. (K e^{j(ωt + Φ)})³ +

（3ωが含まれている）

A_i. (K e^{j(ωt + Φ)})ⁱ +

（i.ωが含まれている）

つまり、このデバイスは、入力信号xには含まれていなかった複数の周波数に対応する信号成分を生成するということになります。

基本波に相当するのは、yの中でωを備えている項です。2ω、3ω、...i.ω、...n.ω（ωの整数倍）の周波数成分はすべて高調波と呼ばれます。これらの高調波は、信号の歪みやノイズの原因になります。 

この状態であれば、それほど大きな問題があるわけではありません。多くの場合、高調波はフィルタで容易に除去できるからです。高調波の成分は、基本波の周りに存在する信号帯域（対象とする信号帯域）から比較的離れた位置に存在するため、フィルタリングが容易になります（図3）。

本当に厄介な問題は、非線形なデバイスと複数の周波数成分を含む入力信号が組み合わせられた場合に発生します。特に、対象とする周波数の近くに擾乱を与える信号が存在する場合には面倒なことになります。以下、2つの周波数成分が存在する場合に何が起こるのかを見てみましょう。つまり、以下のような入力を考えます。 

x = x_a + x_b

ここで、x_aの周波数はω_aで、x_bの周波数はω_bです。この状態の入力信号xは、2トーンの信号とも呼ばれます。 

このxを一般的な式で表すと、以下のようになります。 

y = A₀ + A₁.x¹ + A₂.x² + A₃.x³ +... + A_i.xⁱ +... A_n.xⁿ

上の式の各項は以下に示すように展開することができます。 

• 0次の成分（連続部分）：A₀
• 1次の成分（線形部分）：A₁.x

これらについては、以下の式が成り立ちます。

A₁ × x = A₁.(x_a + x_b)

上の式には、想定どおり周波数ω_aとω_bに対応する元の2つの成分が含まれています。 

• 2次の成分（2乗の部分）：A₂.x²

これについては以下の式が成り立ちます。

A₂.x² = A₂.(x_a + x_b)² = A₂.(x_a² + x_b² + 2. x_a x_b)

x_a²の項には周波数2.ω_a、x_b²の項には周波数2.ω_bに対応する成分が含まれています。これら2つは先述した高調波です。ここでは、それ以外の効果も現れていることに注意してください。つまり、元の各信号を算術的に組み合わせた信号成分が生じます。それらは相互変調積（IM：Intermodulation Product）と呼ばれます。 

2.x_ax_bの項には、周波数ω_a + ω_bと|ω_a - ω_b|に対応する成分が含まれています。元の周波数が同じような帯域に存在する場合、前記の4つの項は比較的遠い位置に現れます。そのため、（安価なフィルタでも）簡単に除去できます。元の周波数が混ざったω_a + ω_b、ω_a - ω_b、ω_b - ω_aは、2次相互変調積（IM2）とも呼ばれます。 

• 3次の成分：A₃.x³

(x_a + x_b)³を展開すると、x_a³、x_b³、3x_a²x_b、3x_ax_b²の項が現れます。これらにより、3ω_a、3ω_b、2ω_a + ω_b、2ω_a - ω_b、ω_a + 2ω_b、2ω_b - ω_aの周波数に対応する別のIMが生じます。元の周波数が混ざった2ω_a + ω_b、2ω_a - ω_b、2ω_b - ω_aは、3次相互変調積（IM3）とも呼ばれます。 

3ω_a、3ω_b、2ω_a + ω_b、ω_a + 2ω_bの項は容易に除去できます。しかし、ω_aやω_bと同じ周波数帯域に存在する2ω_a - ω_bや2ω_b - ω_aといったIM3の項は簡単に除去することはできません。これらの項の1つが情報を搬送する（変調される）場合には、他の項がIM項に干渉しないようにする必要があります。先述したように、これらは対象とする信号帯域内に現れるので、対応が不可能な妨害や干渉の原因になります。 

ここで図4をご覧ください。IM3の項は対象とする帯域内に現れます。そのため、強力かつ高価なフィルタを使用しても簡単に除去することはできません（不可能な場合もあります）。このことが、RFにおいて3次の項が非常に重要になる理由です。シグナル・チェーンのあらゆる個所で3次の項の存在を把握し、その値の測定を行い、それらを最小限に抑えるための方策を適用しなければなりません。 

• 4次の成分：A₄.x⁴

3次の成分と同じように、4次についても、周波数4ω_a、4ω_b、2ω_a + 2ω_b、2ω_a - 2ω_b、ω_a + 3ω_b、3ω_a + ω_b、3ω_b - ω_a、3ω_a - ω_bという成分が現れます。ただ、2次の項の場合と同様に、4次の項による成分はいずれも2つの基本波からかなり離れた位置に現れます。これらのことから、IMについてはnが奇数の場合（つまり、IP3、IP5、IP7など）に大きな問題が生じる可能性があることがわかります。 

• N次の成分：A_n.xⁿ

(x_a + x_b)ⁿの項にも同様の手順を適用することができます。ただ、実際のデバイスでは、高次の項は大きく減衰するので無視することが可能です。この状況は、IM7より上の領域で発生します。ただ、IM5でも無視できる状態になることがあります。 

3つ以上の周波数ω_a、ω_b、ω_cに対応する成分を含むxについて考え、説明を続けることも可能です。しかし、そのような努力をしても、理解を深めることにはつながりません。単にIM2、IM3、IM4などと同様に周波数成分が増えるだけだからです。 

IMからIPへ

上の説明により、IM、特にIM3がどのようにして発生するのかをご理解いただけたはずです。言い換えれば、一般的な測定方法と単位を使ってそれらの値を特定する準備が整ったことになります。ここで、1つ注意しておきたい点があります。それは、「IMnは相互変調積である。IPnは実際の測定値である」というものです。 

上述したように、伝達関数Aのiが1より大きい項はデバイスの線形性が損なわれる原因になります。それらの項の値が大きいほど歪みも大きくなります。したがって、簡略化してA₂、A₃、...A_i...A_nの値だけを測定して評価するという方法も考えられます。 

しかし、それらの絶対値には意味がありません。なぜなら、それらと直線性（対象とする信号A₁）との関連性がわからないからです。言い換えれば、良好なパラメータ（A₁）に対する偏差、より正確に言えばA_i/A₁やA₁/A_iといった比を把握する方が有用です。ここでは、後者について検討することにしましょう。直線性の高いデバイスでは、そちらのほうが高い値が得られるからです。

この方法については、A₀、A₂、あるいはA_iと比較する方法が思い浮かぶ方もいらっしゃるでしょう。しかし、それらのパラメータは役に立ちません。必要なのは直線性の振る舞い（ゲイン、減衰率など）なので、RF技術者が関心を持つのはA₁のみです。

A₁の変化の幅は非常に大きくなる可能性があります。そのため、比を求める場合には単位としてdBまたはdBmを使うと便利です。ここで図5をご覧ください。ここまでに示したy対xの図とは異なり、この図では2つの軸として対数軸を使用しています。ここでは、以下の式について考えています。 

y = A₀ + A₁.x¹ + A₂.x² + A₃.x³ +... + A_i.xⁱ +... A_n.xⁿ

図5からは、以下のことがわかります。 

• A₀の項の値は定数（オフセット）であり、xの値には依存しません。
• A₁xの項は直線の部分です。両対数目盛りのグラフでは、yとxの関係はA₁で決まるオフセットを持つ直線になります。傾きは1dB/dBです。つまりxが2倍になると、yも2倍になります。
• A₂x²の項は2乗項（2次）です。これはA₂で決まるオフセットと、上に示した傾きのちょうど2倍の傾き（2dB/dB）を持ちます。つまり、xが2倍になると、yは4倍になります。
• A₃x³は3次の項です。これは、yとxの関係を表すグラフでは、A₃で決まるオフセットを持つ直線になります。傾きは線形の項と比べて正確に3倍急峻になります（3dB/dB）。つまり、xが2倍になるとyは8倍になります。
• 同様に、n次の項に対応する直線はndB/dBの傾きを持ちます。

上述したように、高次の項になるほど傾きが急峻になります。そのため、高次の線はどこかで1次の線と交差します。この交点がインターセプト・ポイント（IPn）です。 

図5を見ると、デバイスの直線性が高くなるほど、1次の線は（他の線と比較して）グラフ内の高い位置に存在することになるはずです。そのため、IPはより高い位置（IPの値が高い）に現れます。これについては、図6を見れば理解できます。傾きは一定なので、デバイスの直線性が高い場合、n次の項の値は非常に小さくなります。A_nの線がより深い値から始まるので、1次の線と交差するのは軸から遠く離れたところになります。 

図6から、IP2は1次と2次の線が交差する点であることがわかります。同様に、IP3は1次の線と3次の線が交差する点です。より高い次数についても同様です。IPの値はx軸またはy軸で読み取ります。つまり、IPの点を測定する場合、入力インターセプト・ポイント（IIP：Input Intercept Point）と出力インターセプト・ポイント（OIP：Output Intercept Point）の2つの実測値が存在し得るということです。まとめると、以下のようになります。 

• IIPn： 入力電力の軸（x）上で測定したn次のIPの値 
• OIPn： 出力電力の軸（y）上で測定したn次のIPの値 

IIPとOIPの関係

IIPnとOIPnは、同じパラメータであるIPnの値を2通りの方法で表現したものだということがわかりました。ここで、IPnは1次の直線上にあります。このことから、次のような式が成り立ちます。 

Log Y = Log (A₁ X) = Log A₁ + Log X

IPにおいては、以下の式が成り立ちます。 

Log Y = OIP and Log X = IIP

したがって、以下の式が成り立ちます。 

OIP = Log A₁ + IIP

通常、Log A₁はデバイスで規定されている有効なゲインです。したがって、飽和が生じる前の段階では、単純に次の式が成り立ちます。 

OIP_dBm = G_dBm + IIP_dBm

IPの測定と評価

ここで1つ注意すべきことがあります。IPnの点は仮想的なものであり、実際に存在するわけではありません。なぜなら、デバイスは信号が交点に達するかなり前の段階で飽和してしまうからです。ここまでに示したIPnの直線は、実際にはもっと小さいxとyの値から推定された漸近線に相当します。したがって、IPを外挿するための実用的な方法が必要になります。 

IPに近づくレベルの大きな信号を印加できないということは、測定を実施できない（デバイスがそのかなり前の段階で飽和してしまう）ということを意味します。そうなると、より振幅の小さい信号を印加することで必要な値を取得しなければなりません。現実的には、dB（またはdBm）単位の軸を使用してxとyの関係を表す図をベースとして、1次とn次の直線について考えることになります。 

実測を行う際には入力信号P_INを印加します。その振幅は、デバイスが飽和しないように十分小さく設定しなければなりません。それにより、入力に対応する出力P_OUTが得られます。これらの点は、それぞれX軸とY軸に現れます（図7）。 

図7において、P_INは（ジェネレータによって）印加した入力信号を表します。P_OUTは1次の出力信号（測定値）であり、P_{OUT_n}はn次の出力（測定値）です。ここでは、1次とn次の周波数で測定された電力の差をΔP = P_OUT - P_{OUT_n}と呼ぶことにします。 

以下では、印加する信号が純粋な正弦波であるケースを考えます。そこで、式（1）～式（8）にわたる説明内容をもう一度確認してください。すると、次数は周波数によって追跡できることがわかります。実測を行う際には、スペクトル・アナライザを使用することにより、様々な周波数に現れる様々な電力を識別することができます。 

以上で、印加した信号、測定した信号とIPの関係を把握できる状態になりました。ここで図8をご覧ください。この図から、図7の中で4角形として表されている部分には2つの3角形が存在することがわかります。 

2つの3角形の辺は垂直の線を共有しています。両3角形の辺の長さの比は、斜辺の傾きと同じ比になるはずです。つまり、以下に示す一連の式が成り立ちます。 

n/1 = (OIPn - P_OUT + ΔP)/(OIPn - P_OUT)

n = 1 + ΔP/(OIPn - P_OUT)

(OIPn - P_OUT)(n - 1) = ΔP

OIPn - P_OUT = ΔP/(n - 1)

結論として、次式が得られます。 

OIPn = P_OUT + ΔP/(n - 1)

IP3に注目すると、次の式が得られることがわかります。 

OIP3 = P_OUT + ΔP/2

すべての項がdBm単位の値の場合、P_OUT = P_IN + Gであり、OIPn = IIPn + Gです。そのため、以下の式が成り立ちます。 

OIPn = P_IN + G + ΔP/(n - 1)

IIPn + G = P_IN + G + ΔP/(n - 1)

結論として、次の式が成り立ちます。 

IIPn = P_IN + ΔP/(n - 1)

ここで、テストの対象となるデバイス（DUT）としてLNAを使用し、そのIP3を測定するケースを考えます。そのためには、2つの独立した周波数源（ジェネレータ）が必要です。ここでは、それらをGEN-A、GEN-Bと呼ぶことにしましょう（図9）。それらが生成する2つの信号は、振幅は同じで、周波数は非常に近い値であるとします。例えば、ω_aが2.00GHz、ω_bが2.01GHz（両者の間隔は10MHz）といった具合です。あるいは、1MHzと1.001MHzといった周波数を選択することもできます。これについては、実際のDUTに応じて選択します。例えば、欧州のISM帯（Industrial Scientific and Medical Band）向けのDUTであれば約433MHz、GSM（Global System for Mobile Communications）帯向けのDUTであれば約900MHzを選択することになるでしょう。 

まず、GEN-A/GEN-Bによって周波数が異なる2つの信号を生成します。それらの信号はコンバイナ（一種の加算器）に引き渡します。そして、その出力をDUTに入力します。ジェネレータとコンバイナの間と、コンバイナとDUTの間にはフィルタを配置する場合もあります。但し、フィルタは、DUTに入力する2つの周波数源だけに適用するようにしてください。 

次に、スペクトル・アナライザを使用して出力信号を取得します。基本数である2つの周波数成分、すべての高調波、IMが観測されるはずです。     

図10において、P_OUTとΔPは画面上で直接測定できます。また、OIP3 = P_OUT + ΔP/2です。 

図11に示したのは、IP3を測定するために取得したスペクトルの例です。スペクトル・アナライザによって得られる代表的な表示結果を示してあります。 

図11において、M1とM2は2つの基本波を表しています。いずれも振幅P_OUTは約-11dBmとなっています。一方、M3とM4はIM3の成分です。振幅はいずれも約-45dBとなっています。したがって、以下のような計算が成り立ちます。 

ΔP = -11 - (-45) = 34 dB

ここで、ΔPはM1（またはM2）とM3（またはM4）の電力の比（単位はdBc）です。 

このことから、OIP3の値は以下のようになります。 

OIP3 = -11dBm + 34/2 dB

これを計算すると、以下のように値が求まります。 

OIP3 = -11dBm + 17dB = +6dBm

このDUTは7dBのゲインを備えているとします。そうすると、IIP3の値は以下のようにして求められます。 

IIP3 = OIP3 - G = 6 - 7 = -1dBm

この結果から、このDUTは標準的かつ性能が良好なLNAだと言えます。 

具体的な製品の例

ここで、具体的な製品の例を紹介することにします。例えば、レシーバーのRFフロント・エンドでは、初段のデバイスとしてIP3が非常に高いものが必要になることがあります。そのような場合には「MAX2062」を利用するとよいでしょう。

同ICは、対応周波数範囲が50MHz～1000MHzの可変ゲイン・アンプ（VGA）です。デュアルチャンネルの製品であり、優れた直線性を達成していることを特徴とします。このような仕様であることから、多様なRF/IFアプリケーションに応じて回路を構成できます。例えば、PA用のプリドライバ、IF対応のダイバーシティ・アンプ（デュアル構成であるため）、マルチパスのアプリケーションやトランスミッタのアプリケーション向けのVGAなどの用途に適用可能です。このICは、OIP3が41dBm、OIP2が56dBmという卓越した直線性を備えています。2つの信号パスのそれぞれには、24dBの高ゲイン・アンプとユーザがプログラム可能な2つの減衰器（1つはデジタル制御、もう1つはアナログ制御）が配置されています。そのため、1dBステップで最大64dBまで調整可能な動的ゲイン範囲が得られます。また、それらすべてのブロックはアクセスが可能なRF入出力を備えています。したがって、最良のNF（ノイズ指数）、最良のOIP3、またはそれらを組み合わせて最良の条件が得られるよう簡単に調整することができます。 

MAX2062のデータシートにはOIP3の評価方法が示されています。それによれば、振幅が0dBmの2トーン信号が使われています。一方の信号の周波数は、50MHz、100MHz、200MHz、350MHz、450MHz、750MHz、900MHzの7種です。それぞれと対を成すものとして、周波数が1MHz異なる信号が使われます。この7種の条件の下、OIP3の評価が行われています。 

カスケード接続された回路のIPn

個々のデバイスのIPnを把握できたとします。では、それらを縦列（カスケード）に組み合わせた場合、全体としてのIPnはどうなるのでしょうか（図12）。 

図12の回路では、複数の機能ブロックをカスケード接続しています。この回路全体のゲインは次のようになります。 

G = G1 × G2 × G3 (リニア・スケール)

これをdB/dBm単位で表した場合、以下のようになります。 

g = g1 + g2 + g3 (dB/dBm単位)

この式を使用すると、トータルのOIPnは以下のような式で表すことができます。 

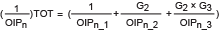
（導出方法は割愛します） 

-1dB圧縮ポイント

本稿の冒頭で述べたように、IPnはデバイスの直線性を特徴づける唯一の方法です。ただ、-1dB圧縮ポイント（CP1またはCP1dB）も非直線性を測定する性能指標として使われています。CP1は、実際の入出力特性の曲線が直線の漸近線から1dBだけ外れる（つまり、低下する）点を表します（図13）。 

また、CP1は、実際の曲線が漸近線を1dB下げた直線と交差する点だと見なすこともできます。CP1については、入力側はICP1、出力側はOCP1として表されます。CP1とIP3の間には厳密な関係はありません。ただ、CP1はIP3の値と強い関連性を示すということもわかっています。一般的に言えば、次式が成り立ちます。 

OCP1 = OIP3 - x

ここで、xは通常-8dBから-12dBの間の値です。 

ここで1つの例を考えてみましょう。「MAX2645」は汎用性の高いLNA製品です。この製品は、ゲインが15.2dBのPA用プリドライバとして構成できます。その場合、ICP1は-1.8dBmとなります。一方、同じセットアップにおけるIIP3は11.8 dBmとなります。つまり。IIP3とICP1には13.6dBの差があることがわかります。 

まとめ

本稿では、IIPnやOIPnの定義について詳しく解説しました。また、それらと入出力電力、ゲインとの関係なども明らかにしました。本稿で示した分析は、スペクトル・アナライザを使ってIP3の値を実測する際には必要ありません。しかし、予期せぬ問題や、システム全体で見た場合に不合理な結果に直面することもあるはずです。そうした場合には、本稿で説明したようなより深い考察が必要になる可能性があります。そのような際には、ぜひ本稿の内容を参考にしてください。