Isolating SPI for High Bandwidth Sensors
SPI (serial peripheral interface) busses are a favorite of designers for many reasons. The SPI bus can run at high speed, transferring data at up to 60 Mbps over short distances like between chips on a board. The bus is conceptually simple, consisting of a clock, two data lines, and a chip select signal. Since data is presented on one phase of the clock and read back on the opposite phase, there is a significant margin for delays and mismatches in speed. Finally, the bus is composed of unidirectional lines, which simplifies implementation in a microprocessor eliminating flow of control concerns and lending itself to isolation with optocouplers or digital isolators, since isolators are inherently unidirectional devices.
In industrial applications, such as thermal or pressure monitoring systems, communication with the ADC in the sensor front end does not require a high sample rate and, hence, a high SPI clock rate. Even isolated designs are simple to implement in a wide variety of isolation technologies, but requirements evolve with time. The venerable SPI interface has been pushed to its limits by applications with long wire runs, high data rates, and isolation requirements as well. In this article, we will look at the SPI bus, its constraints, and how to deal with them in isolated systems.
An application that pushes the limits of isolated SPI performance is the high dynamic range sensor interface. To create a system with wide dynamic range, a designer would start with an ADC with a good signal-to-noise ratio (SNR), which is usually related to the word length; 16 bits is common for converters. But where higher dynamic range is required, other techniques can be employed, such as variable gain amplification of the input and oversampling. Oversampling will trade bandwidth for noise rejection. If the sample frequency is doubled, typically the noise performance is improved by 3 dB. For example, a 75× oversample rate will give an improvement in noise performance and dynamic range of about 18 dB. A 75× oversample of a signal means that an ADC running at 900 kSPS would give 18 dB better dynamic range over about a 6 kHz band width. The bandwidth and dynamic range can of course be traded off, but in the end, running the ADC as fast as possible has great benefits. This implies that the SPI bus will have to keep up with this avalanche of data. Let’s work through an example with a typical component used for high sample rate applications, such as the ADI AD7985 pulsar ADC which can run up to 2.5 MSPS and see how talking to it through an SPI bus affects the performance of the signal chain.
ADC Interfaces
The typical analog-to-digital converter handles data in two basic operations shown in Figure 1. First, the ADC has a conversion period (tCONV) where it goes through its internal procedure to create a digital word that represents the voltage at its input. Second, the ADC transfers the acquired data word through a digital interface to a controller during the acquisition time (tACQ). The ADC will usually have a minimum cycle time (tCYC) before it can start another conversion that is about the sum of tCONV and tACQ but can be shorter when the ADC has special transfer modes that let acquisition and transfer overlap. For simplicity, the following discussion will be based on sequential conversion and acquisition.

Figure 1. Simple ADC Transfer Sequence.
The conversion time and minimum cycle time are the same no matter how the data is transferred. But the acquisition time depends on the properties of the data interface, in most cases the operation of the SPI bus. If the acquisition time is lengthened due to clock rates on the SPI, the sample rate of the ADC can be severely limited.
SPI Clock Rate Limitations
The SPI link between a microprocessor/FPGA (MCU) and an ADC is illustrated in Figure 2. The SPI bus consists of the connections between a pair of shift registers, one in the master MCU and one in the slave ADC. The MCU provides a clock that synchronizes the transfer. One edge of the clock shifts data out of the shift registers and the complementary edge clocks the data that has been presented into the other end of each shift register in a ring topology. In the case of an ADC, there may not be a need to shift data from the MCU to the ADC so this channel has been eliminated for simplicity along with the slave select. The ADC fills its internal shift register during the conversion phase of operation then shifts the register out during the acquisition phase.

Figure 2. ADC SPI Communication Block/Timing Diagram
In an SPI transaction, the clock signal generated by the master travels to the slave through some wiring delays where it triggers the slave to shift out its data after some internal delay. The data signal travels back to the master again through wiring delays where it must arrive at the master in time for the complementary edge of the clock. The master typically has some additional setup time requirements on this line. This timing is illustrated in Figure 2 and it shows that these delays establish the minimum time for half of a master clock period. In non isolated systems, these times are typically very short, in most cases <10 nS, and allow the SPI clock to run at speed in excess of 50 MHz.
If an isolation barrier is added to the SPI data path, as shown in Figure 3, it adds terms similar to the trace delay. However, depending on the technology used for isolation, the signal propagation delay (prop delay, tpISO) through the isolation can be in excess of 100 nS. Figure 3 also shows how the new set of delay times extend the time required for a data transaction and significantly increase the half period of the SPI clock. The isolation delays dominate all other time delays in the system and the maximum clock frequency can drop to a few MHz.

Figure 3. Isolated ADC SPI Communication Block/Timing Diagram.
The primary constraint on the clock period is the requirement that data is present at the master in time for the next clock edge. In nonisolated systems this is not much of a constraint, and it actually adds to the robustness of the data transfer by allowing generous timing margins. However, once the propagation delay of the data path starts to dominate the half period, it severely degrades the maximum speed of the bus.
Luckily there is a way around this limitation. If the data returning from the slave has an independent clock synchronized to it, a separate receiving shift register can be set up in the MCU to accept data based on the independent clock. In this case, the throughput of the SPI bus is no longer limited by the propagation delay of the isolation barrier, but by the throughput of the isolator.
The independent clock, DCLK, can easily be created by adding a matched high speed data channel to the isolator and sending a copy of the isolated SPI clock along a matched data path with the data from the ADC as shown in Figure 4. This approach does require additional hardware in the isolation barrier; an additional isolation channel and an independently clocked shift register in the MCU. The MCU reads data from the secondary receiving register rather than the standard SPI register.

Figure 4. Isolated System Creating an Independent Data Clock.
To illustrate how this data transfer method can be implanted in different technologies, the following three examples are examined quantitatively for maximum speed, and qualitatively for power consumption and required board space. We will see that the while in standard isolated SPI, it is the round trip propagation delay that limits the speed, and in the delayed clock scheme, it is the timing skew and distortion in the isolator that sets the limit.
Optocoupler Implementation
In typical industrial applications, single-channel digital optocouplers are frequently used in isolating high speed buses. Four optocouplers are needed to isolate a standard 4-wire SPI bus. The timing parameters important in estimating the max SPI clock speed in a popular industrial CMOS optocoupler are:
- Maximum data rate of 12.5 Mbps or a minimum pulse width of 80 ns.
- Maximum propagation delay (tpISO) of 40 ns.
- Maximum pulse width distortion (PWD) of 8 ns.
- Maximum part to part propagation delay skew (tPSK) of 20 ns. This parameter is important since multiple optocouplers are used to create the isolated SPI bus.
To estimate the SPI throughput, we assume some typical delays for the different components in Figure 3. Each trace delay is assumed to be 0.25 ns, amounting to a total trace delay (tTRACE) of 1 ns. Similarly, the slave delay (tSLAVE) and master setup delay (tMASTER) are assumed to be 3 ns and 2 ns respectively.
Therefore, from our discussion of isolated SPI clock rate in Figure 3, for an SPI bus isolated using the above optocoupler, half the SPI clock period will be

or 86 ns—resulting in an SPI clock rate of 5.75 MHz or slower and making it clear that the 2 × tpISO considerably slows down the SPI bus speed.
Now, consider adding an extra isolator in the reverse direction to route the isolated clock signal back to the master and implement the delayed clock as shown in Figure 4. This allows us to generate a clock signal in sync with the returned data from the slave. The round trip propagation delay [2 × tpISO] of the isolator no longer limits the clock rate. With the remaining delays in the system, can the isolated SPI half clock period be ≥ [tTRACE+ tSLAVE+ tMASTER] ns or 6 ns, supporting a maximum SPI clock rate of 80 MHz? Unfortunately, the answer is not that simple.
Asymmetries in forward and reverse channels must still be accounted for when calculating the minimum SPI clock period shown in Figure 5 as tSKEW. The propagation delay skew between parts and the pulse width distortion limit the new SPI half clock period to

or 62 ns. This results in a real maximum clock rate of 8 MHz. However, due to its 80 ns minimum pulse width limitation, this optocoupler can only support a maximum SPI clock of 6.25 MHz. The above example illustrates that even if the optocoupler wasn’t constrained by its minimum pulse width, the tSKEW severely limited the maximum SPI clock rate from a possible 80 MHz with a perfect delay match to 6.25 MHz in the actual application.
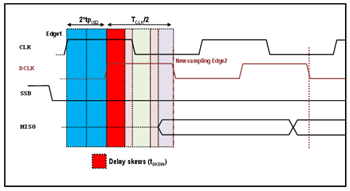
Figure 5. Practical DCLK Timing Diagram.
Can using a faster optocoupler with a shorter minimum pulse width help? A very high speed optocoupler with a minimum pulse width of 20 ns can allow us to run the previous interface at a higher rate. But even these devices suffer from large skew and distortion parameters. With a tPSK of 16 ns and PWD of 2 ns, the minimum SPI clock half period turns out to be ≥ 42 ns, resulting in a maximum clock rate of 11.75 MHz. In both the above cases, the timing characteristics of the optocouplers further degrade over time, thereby introducing more mismatches between delayed clock and slave data. Adding timing margin for these variations results in requiring further reduction of the SPI clock rate.
Using an additional fast optocoupler for SPI isolation, besides being very expensive, also demands a lot of board area since these devices are typically single channels in SO8 packages and 5 channels are required. The power budget for the isolated interface can be as much as 20 mA of current per channel.
Digital Isolator Implementation
Over the past decade a new generation of digital isolators has become available. These devices have higher integration, higher speed, lower propagation delay, low skew, and less distortion. Consider a quad-channel digital isolator—the 3 forward channels and 1 reverse channel allow for compact isolation of a 4-wire SPI bus. Similar to the optocoupler example, we obtain the following timing parameters from the data sheet; a minimum pulse width of 11.1 ns (90 Mbps), max propagation delay (tpISO) of 32 ns, max pulse-width distortion (PWD) of 2 ns, and max propagation delay skew between parts (tPSK) of 10 ns. But, unlike the single-channel optocouplers, in a quad-channel digital isolator, the channelto-channel matching between a pair of opposing directional channels also needs to be considered. In the above part, this parameter (tPSKOD) is 5 ns.
Using the same typical delays for Figure 3, the half clock period for an isolated SPI bus using the digital isolator should be

or 70 ns, with a maximum clock of 7 MHz. Like with the optocoupler case, we see the SPI rate to be heavily constrained by the propagation delay of the isolator. But digital isolators, built in standard CMOS technology, have very stable timing characteristic across product lifetime. This lets us set the SPI clock rate without leaving much margin for variations in the timing characteristics.
If an extra isolator channel is used to implement the delayed clock as per Figure 4, at a minimum, an additional high speed channel needs to be used. The SPI throughput again depends on the mismatches and distortion between the clock and data channels. Given the timings of all of the channels is similar, the new SPI half clock period should be

or 25 ns, for a maximum clock rate of 20 MHz.
In many applications, the MCU only shifts out data from an ADC and doesn’t shift-in anything. In such 3-wire SPI buses, a single quad digital isolator with 2 reverse channels can be used to implement the SPI bus and the delayed clock. In these cases, there is an added benefit. The half SPI clock period will be

or 20 ns, resulting in an even faster maximum clock rate of 25 MHz.
Although the speed and skews of the digital isolators are significantly better than that of optocouplers, timing skews and distortions between channels still limits the maximum possible SPI clock rate. The extra isolator to delay the clock still consumes around 20% to 25% more power. Thus, using existing isolators, will cost more power and board space while still falling short of the maximum possible benefit of the scheme.
Optimizing The Digital Isolator Delayed Clock Implementation
Analog Devices has developed a digital isolator optimized to deliver the highest possible performance in the delayed clock scheme. The ADuM3150 (Figure 6) is part of the SPIsolator™ series of high speed digital isolators designed to optimize the isolation of SPI buses. The ADuM3150 generates a delayed clock, DCLK, without the use of an extra isolator channel. The DCLK is generated by delaying the standard SPI clock by an amount equal to the round trip propagation delay [2 × tpISO] through the isolator. Figure 6 shows the internal block diagram of the ADuM3150. The delay cell is carefully trimmed at production to match the round trip prop delay through the part, thereby minimizing the timing mismatch between delayed clock and returning slave data. The delay mismatch is not only considerably minimized but also very well defined across wide operating conditions and is guaranteed in the data sheet by the DCLKERR parameter.

Figure 6. ADuM3150 SPIsolator Delay Clock Implementation.
The DCLKERR is a measure of how much the delayed clock is out of sync with the slave data and therefore the sign of the DCLKERR indicates whether the delayed clock leads or lags slave data. Since the delayed clock is used to sample the slave data into the master, it shouldn’t lead the data. DCLK lagging the data is acceptable as long as it doesn’t miss sampling the data bit altogether. The ADuM3150 data sheet specs the DCLKERR between –3 ns and 8 ns and the PWD at 3 ns. Accounting for maximum leading DCLKERR and PWD, the SPI clock rate is

or 12 ns, a maximum clock rate of 40 MHz. ADuM3150, with a maximum data rate of 40 MHz, is able to match this high SPI clock rate without any of the size, cost, and power penalties associated with using an extra isolator channel.
| Clock delay mechanism | Major tSKEW contributors | Max SPI speed (MHz) | Remarks/Comments |
| Single-channel Opto1 tpISO = 40 ns | PWD = 8 ns tPSK = 20 ns |
6.25 | • Large board area • High power • Timing characteristics vary over lifetime • High cost |
| Single-channel Opto2 tpISO = 20 ns | PWD = 2 ns tPSK = 16 ns |
11.75 | • Large board area • High power • High speed optos very expensive • Timing characteristics vary over lifetime • Very high cost |
| Digital isolator tpISO = 32 ns | PWD = 2 ns tPSK = 10 ns tPSKOD = 5 ns |
25 | • Moderate to high board area in 4-wire SPI case • High power • Moderate cost |
| Integrated delay
digital isolator: ADuM3150 tpISO = 14 ns |
PWD = 3 ns DCLKERR = 3 ns |
40 | • No added board area • Lowest power • Minimum tSKEW, due to trimmed delay • Well characterized DCLKERR • Lowest cost |
Conclusion
In order for oversampling to be a useful tool in increasing dynamic range in sensor applications, there must be a high enough multiplier of the sampling frequency compared to the frequency of interest to provide significant noise reduction. The delayed clock scheme presented here provides a path to improving the throughput of an isolated SPI interface and increase sample rates. This method will provide a boost to the max SPI clock rate across the available isolation technologies. The digital isolation technology provides significant advantages over the older optocoupler because of the tight control of skew between channels and other distortions in the signal chain. ADI has taken this technology further by optimizing an SPI specific isolator, the ADuM3150, to provide low skew integrated delayed clock function without the overhead and power consumption of the older technologies and methods. This will enable sample rates of up to 1 MSPS when paired with a fast ADC by allowing up to 40 MHz data transfers though the isolated SPI port. The ADuM3150 is part of a series of SPI specific digital isolators that improves integration with the high channel count ADuM3151/ADuM3152/ADuM3153 as well as the added functionality of the ADuM3154 that supports multiple isolated slaves.




















