半導体による高精度の温度検出 −±0.1ºC単位の温度測定に関する自叙伝的考察
概要
本稿では、最新世代の半導体温度センサーの精度について検討します。これらのセンサーはデジタル出力で、リニアライゼーションを必要とせず、パッケージ・サイズが小さい上に低消費電力です。その多くは、アラーム機能を使ってシステムに故障の可能性を警告するようにプログラムすることができます。
はじめに
電子産業ではこれまで以上のレベルの精度が求められており、これは温度検出についても例外ではありません。温度検出ソリューションは数多く存在し、それぞれに長所と短所があります。半導体温度センサーは非常に高い直線性を備えていますが、他のソリューションのような精度は望めませんでした。しかし、半導体温度検出における最近の進歩により、半導体ソリューションを使って高い分解能と精度を実現することは可能になったと言えます。
新しい冷凍庫
2020年3月、英国ではまさにロックダウンが開始されようとしていました。世の中はスーパーマーケットの閉鎖に備えて食料の買いだめに動いており、この先どうなるのかは不透明でした。そんな折、ブランブル家の冷凍庫が動かなくなってしまいました。オンラインで新しい冷凍庫を探す私の頭の中には、ケニー・ロジャースの歌「ルシール」にある「なんて時に出て行っちまったんだい…」という歌詞がリフレインしていました。数日後に届いた新しい冷凍庫のフロント・パネルにはデジタル温度計が取り付けられていましたが、これはブランブル夫人のご希望でした。推奨温度設定は–18ºCで、1時間後には設定温度になって食品を入れる準備が整いました。私は温度の指示値には懐疑的でしたが、食品を凍らせることができる限り気にしませんでした。しかし、問題が1つありました。エンジニアというのは常に何かが気になるものですが、見かけは賢人のようなデジタル表示がじっと私を見つめ、その自信ありげな指示値で私に挑んでいるように感じられた数日が過ぎると、とうとう我慢ができなくなりました。我が家のキッチンに新たに加わったこの冷凍庫が謳う精度を、テストしないではいられなくなってしまったのです。
温度センサー
産業用アプリケーションに使われている温度センサーには様々な種類があり、それぞれに長所と短所があります。これらの温度センサーの動作については詳しい文献が多数存在するので、ここで詳細を繰り返すことはしませんが、概要を以下に示しておきます。
熱電対
熱電対は低コストで中程度の精度を備えており、非常な高温の測定に使われます。これらのセンサーは、それぞれ異なる金属で作られた2つの接点を異なる温度に維持したときに生成される電圧に依存しています。この原理は1821年にトーマス・ゼーベックにより発見されました。K型熱電対(クロメル合金とアルメル合金を使用)の場合は約41µV/°Cの電圧を出力し、1000°Cを超える温度の測定に使用できます。ただし、ゼーベック効果は2つの接点の温度差に依存するので、高温側接点で温度を測定する間、低温側接点を既知の温度に保つ必要があります。皮肉なことに、温度差を測定するためには低温接点にもう1つの温度センサーが必要で、これにはAD8494のようなデバイスが適しています。熱電対は物理的に小さいので熱質量も小さく、温度変化に素早く反応します。
RTD
中程度(500°C未満)の温度を測定する場合、産業界では測温抵抗体(RTD)が広く使われています。これらのデバイスは、抵抗値が温度と共に増大する金属製の素子で構成されており、通常は白金(Pt)が使われます。実際、産業界で最も多く使われているのがPT100センサーで、この名前は、白金製で0°Cでの抵抗値が100Ωであることから付けられたものです。これらのデバイスは熱電対のような高温測定には使用できませんが、高い直線性を備えており、指示値の再現性も優れています。PT100には高精度の駆動電流が必要です。この電流は、温度に比例した正確な電圧降下をセンサーに発生させます。PT100の接続ワイヤの抵抗はセンサーの抵抗測定に誤差を発生させるので、ケルビン検出が一般的であり、3線式または4線式のセンサーが使われます。
サーミスタ
低コストのソリューションが必要で測定温度が低い範囲の場合は、ほとんどがサーミスタで十分です。これらのデバイスは非線形性が強く、スタインハート・ハート式(Steinhart-Hart equation)に基づく特性を有しており、温度の上昇と共に抵抗が減少します。サーミスタの利点は、温度変化が小さくても抵抗の変化が大きいことです。そのため非線形性があるにも関わらず、高い精度を実現することができます。また、熱応答が速いこともサーミスタの特徴です。個々のサーミスタの非線形性は正確に分かっているので、LTC2986などのデバイスを使って補正することができます。
至るところにダイオードはあれども、(Vbeが)下がるものは1つもなし…
最終的に、我が家の新しい家電品の正確さをテストするために私が選んだのは、半導体温度センサーでした。これらのセンサーは、そのまますぐに使用することができます。冷接点温度補償やリニアライゼーションは不要で、アナログ出力とデジタル出力を使用でき、キャリブレーションも事前に行われています。しかし最近まで、その精度はそれほど高くありませんでした。電子機器が正常な状態にあるかどうかを示すには十分な精度は備えていましたが、例えば±0.1°C程度の精度が求められる体温などの測定には不十分でした(ASTM E1112標準による)。この状況は、±0.1°Cの測定分解能を持つADT7422と、±0.2°Cの測定分解能を持つADT7320半導体温度センサーの出現によって変わりました。
半導体温度センサーは、トランジスタのVbeの温度依存性を利用しています。この依存性は、エバース・モル式(Ebers-Moll equation)によって次のように近似されます。

ここで、Icはコレクタ電流、Isはトランジスタの逆飽和電流、qは電子の電荷(1.602 × 10–19クーロン)、kはボルツマン定数(1.38 × 10–23)、Tは絶対温度です。
式1のコレクタ電流を表す式はダイオードの電流についても当てはまりますが、では、なぜすべてのアプリケーション回路がダイオードではなくトランジスタを使用しているのでしょうか。実際には、ダイオード内の電流には、電子がpn結合の空乏領域を通過する際にホールと再結合することによって生じる再結合電流も含まれており、これがVbeと温度に伴う非線形性をダイオード電流に生じさせます。この電流はバイポーラ・トランジスタにも生じますが、これはトランジスタのベースに流れ込むのでコレクタ電流には表れてきません。したがって、非線形ははるかに小さくなります。
上の式を変形すると次式が得られます。

IsはIcと比較すると小さいので、式2の「1」の項は無視することができます。これにより、Vbeの変化はIcの対数変化に対して直線的になることが分かります。また、kとqは一定であるため、IcとIsが一定ならば、温度に対するVbeの変化が直線的になることも分かります。トランジスタに流れ込むコレクタ電流を一定にして、Vbeが温度と共にどのように変化するかを測定することは、難しくありません。
Isはトランジスタの形状に関係しており、温度に大きく依存します。多くの半導体デバイス同様、その値は温度が10°C上昇するごとに2倍になります。この変化が電流にもたらす影響は対数関数によって低減されますが、Vbeの絶対値はトランジスタごとに異なるので、キャリブレーションが必要になるという問題が残ります。したがって、実際の半導体温度センサーでは2つの同じトランジスタを使って、一方のトランジスタへのコレクタ電流を1 × Icに強制し、他方を10 × Icに強制しています。集積回路内で同じトランジスタとレシオメトリック的に正確な電流を作り出すことは容易であり、ほとんどの半導体センサーがこのアーキテクチャを使用している理由もここにあります。電流の対数的変化によってVbeが直線的に変化し、Vbeの差が測定されます。
式2から、2個のトランジスタを同じ温度に保った場合、これらのVbeの差は次式で与えられます。

したがって、

以上から次式が得られます。

各トランジスタに異なる電流を流してVbeの違いを測定することにより、非線形のIs項、Vbeの絶対値の違いによる影響、およびトランジスタの形状に関係するその他の非線形性の影響が除去されました。k、q、およびln10はすべて定数なので、Vbeの変化は絶対温度に比例します(PTAT: Proportional To Absolute Temperature)。電流の10倍の変化に対し、2つのVbeの差は温度と共に約198µV/°Cで直線的に変化します。これを実現する回路の簡略図を図1に示します。

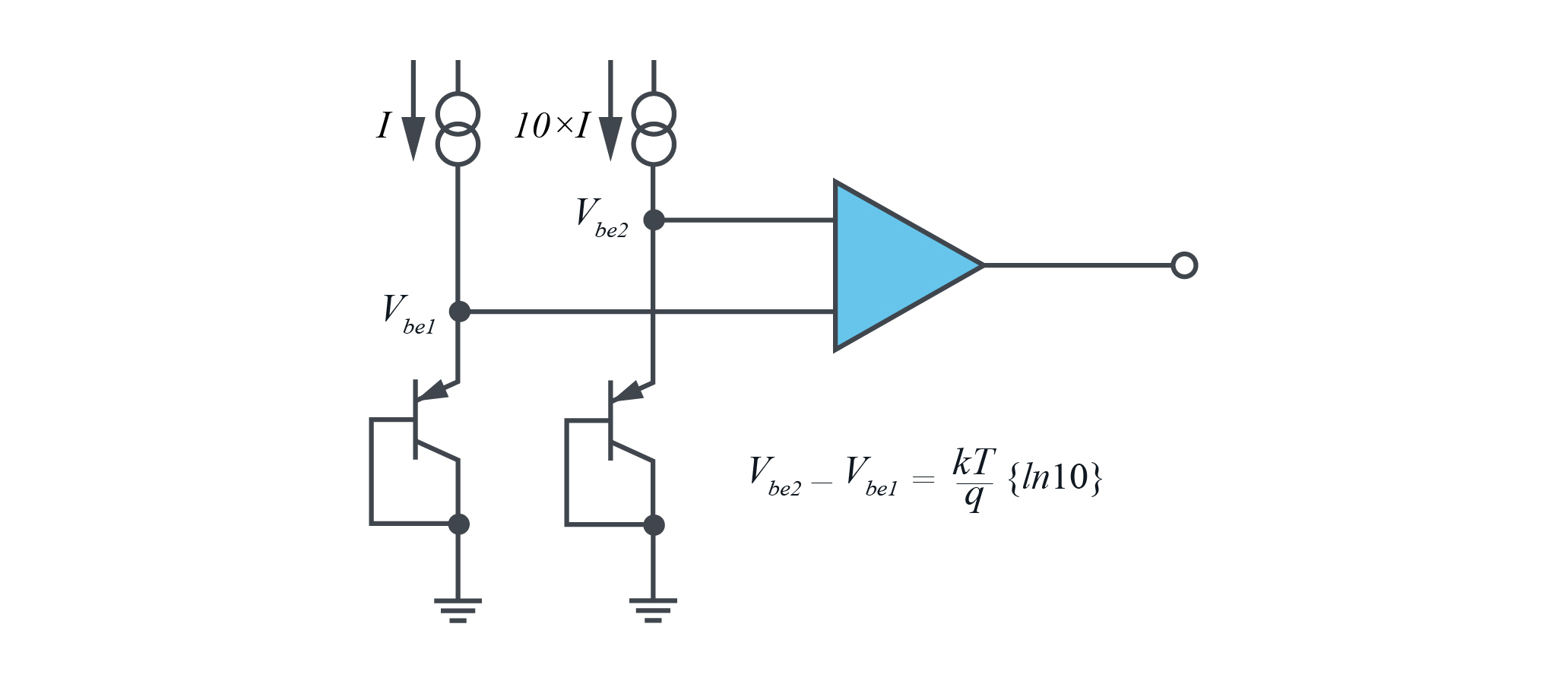
図1. 温度を測定するための基本的回路
図1の電流は慎重に選ぶ必要があります。電流が大きすぎると、トランジスタ内にある内部抵抗の著しい自己発熱と電圧降下によって、正しい結果が得られなくなります。逆に電流が小さすぎると、トランジスタ内のリーク電流によって誤差が非常に大きくなります。
また、上に挙げた式はいずれもトランジスタのコレクタ電流に関係するのに対して、図1では一定のエミッタ電流がトランジスタに流されている点にも注意する必要があります。トランジスタは、コレクタ電流とエミッタ電流の比率が確定される(なおかつ1に近い値となる)ように設計できるので、コレクタ電流はエミッタ電流に比例した値となります。
これは話の開始点に過ぎません。半導体温度センサーで±0.1°Cの精度を得るには、広範な特性評価と調整を行う必要があります。
鳥だ! 飛行機だ!
いや、スーパー温度計だ! そう、そんな温度計は存在します。未補正の半導体温度センサーは、シリコン油で満たした槽に入れて正確な温度値まで加熱し、補正する必要があります。この場合の温度測定はスーパー温度計で行います。これらのデバイスは、小数点以下5位以上の精度で測定を行うことができます。センサー内のヒューズを切って温度センサーのゲインを微調整し、式y = mx + Cに基づいてその出力を直線化します。シリコン油は温度分布が極めて均一なので、ほとんどのデバイスを1回で補正することができます。
ADT7422は、25°C~50°Cの温度範囲で±0.1°Cの精度を備えています。この温度範囲は人体の標準体温に近い38°Cを中心としていることから、ADT7422は正確なバイタル・サインのモニタリングに最適です。また、ADT7320は工業用アプリケーション向けとして±0.2°Cの精度に調整されていますが、ADT7422より広い–10°C~+85°Cの範囲で使用できます。


図2. 厚さ0.8mmのPCBに取り付けたADT7422
しかし、問題は半導体温度センサーのキャリブレーションだけではありません。極めて高精度の電圧リファレンスが必要とされるのと同様、ダイに加わるストレスはセンサーの精度を損なう可能性があり、PCB、リード・フレーム、プラスチック・モールディング、露出パッドなどの熱膨張もすべて考慮に入れる必要があります。ハンダ処理プロセスにも、固有の問題がいくつかあります。ハンダのリフロー・プロセスは部品の温度を260°Cまで上昇させるので、プラスチック・パッケージを軟化させると共に、ダイのリード・フレームに歪みを生じさせます。したがって、部品が冷却されてプラスチックが再硬化すると、ダイに機械的応力が封じ込められる結果となります。アナログ・デバイセズのエンジニアは数ヵ月の時間をかけて精緻な実験を繰り返し、PCBの厚さは0.8mmがスイート・スポットであり、ハンダ処理後でも±0.1°Cの精度を実現できることを発見しました。
私のソーセージは正確には何度で冷凍されているのか
私はADT7320をマイクロコントローラとLCDディスプレイに接続して数百行のCコードを記述し、センサーを初期化してデータを取り出しました。ADT7320は、32個の1を連続してDINピンに書き込むことによって、簡単に初期化できます。設定レジスタは、ADT7320が16ビットの精度で連続して変換を行うように設定しました。ADT7320から一度データを読み出した後は、次の変換を行えるようにするまでに少なくとも240msの遅延が必要です。非常に低速のエンド・マイクロコントローラも使用できるようにするために、SPIは手動で記述しました。このADT7320を冷凍庫の中に約30分間置いて、我が家の新しい冷凍庫の中が最終的に何度に落ち着いているのかを調べました。図3は、冷凍庫内の温度が–18.83°Cであることを示しています。


図3. –18.83°Cの冷凍庫内温度
このようなレベルの温度精度で食品を保存する必要はありませんが、これは感動的な精度だと思います。更に私は、ある夏の日にオフィスの温度を測定しました。図4に示すように、その指示値は22.87°Cでした。


図4. 22.87°Cのオフィス室温
まとめ
半導体温度センサーは長い道のりを経て極めて正確なものとなり、非常な高精度でバイタル・サインをモニタリングすることも可能になりました。これらのセンサー内部を構成する技術は、しっかりと確立された原理に基づいていますが、それを使用して1°C未満の精度レベルを実現するために必要な調整を行うには、大変な努力が求められます。このレベルの精度が実現できたとしても、機械的ストレスやハンダ処理は、何時間もかけて実現した成果を簡単に帳消しにしてしまうおそれがあります。
ADT7320とADT7422は、PCB上にハンダ付けした後でも1°C未満の精度レベルを実現することができるように行われた多年にわたる特性評価の結晶とも言える製品です。
著者について
{{modalTitle}}
{{modalDescription}}
{{dropdownTitle}}
- {{defaultSelectedText}} {{#each projectNames}}
- {{name}} {{/each}} {{#if newProjectText}}
-
{{newProjectText}}
{{/if}}
{{newProjectTitle}}
{{projectNameErrorText}}