はじめに

以降の 2 冊の技術ノートでは、アナログ入力段（アナログ・フロントエンド）こみで ADC（Analog to Digital Converter）でのノイズ特性最適化をどうするかについて、NF（Noise Factor/Noise Figure）を指標として考察してみます。

なおこの技術ノートでは「前段の増幅回路（フロントエンド）と ADC とのシステム」を「系」と表現します。

白状いたしますと（汗）【その 1】

かなり前の話しですが、アナログ・フロントエンド（信号源の電圧・電流を増幅したりフィルタしたりする、系の前段の信号処理回路）から ADC 入力に現れるノイズ電圧実効値レベルの求め方について、とあるセミナーでお話ししたことがありました。

それはこの技術ノートでも説明するような方法、つまり SPICE シミュレーションを用いて、1Hz あたりの出力ノイズ電圧密度スペクトルを得て、それを電力密度にして周波数領域で積分することで、アナログ・フロントエンド出力のノイズ電圧実効値レベルを求められます、というお話しでした。そして（以降でも示す話しですが）ADC 自体の入力換算ノイズ・レベルはデータシートに記載されていますので、それらにより「相互の比較ができます」という結論をお話ししました。

しかしそのときに「求め方は分かった。それではどうすれば最適状態を実現できるか」というご質問をいただいたのです。「そういえば何かの書籍に書いてあったな」とそのときは思ったものの、適切な応答ができませんでした。

その後もことあるごとに、これをどう考えれば良いのか、また「どの書籍に書いてあったのかなぁ」と長く彷徨っていました。とあるときに、ふと「そうだ」と思い立ち式を立ててみて、「あー、なるほど…」と納得し、この技術ノートを書けるまでに至ったのでした。ということで「白状いたしますと、最初は分かっていせんでした」（汗）。

白状いたしますと（汗）【その 2】

上記で「何かの書籍に…」と示したように、手持ちの蔵書のどこかに書いてあった記憶はあったのですが、これも白状すると（すでにしていますね…汗）なかなか当該箇所を見つけることができませんでした。この技術ノートを執筆するなかで、想定される書籍をあらためて数冊ひっくり返しながら探してみると、 図 1 の書籍[1]に記載があることが分かりました！

なんとご丁寧にそのページには、誰だか知りませんが…付箋を張ってあります（笑）。当時も印象が強かったのでしょう。しかし改めて見てみると、この技術ノート・シリーズにおける NF に関する検討からすると、「ちょっと導出がおかしそうだな」と感じさせるものでした。付箋を張ったときは、式の背景を見出すことができず、衝撃的な（？）印象を受けたのでしょうが、背景を解釈できると、印象も変わってくるものです…。

これまでの 2 冊の技術ノートでは

これまでも2冊の技術ノートで NF について考えてきました。そこではRFシステムなどが例となる『50Ωで整合終端された系』の NF 計算、つぎに OP アンプ増幅回路などが例となる『整合終端ではない系』のNF計算、さらに『カスケード接続した50Ωで整合終端された系全体』のNF計算、つづいて『カスケード接続した整合終端ではない系全体』のNF計算を見てきました。

『50Ωで整合終端された系』では、カスケード接続してもしなくても、各段の信号源側（前段の出力）インピーダンスは50Ωになっていました。そのためそれぞれの信号源抵抗のサーマル・ノイズは50Ωで決定することになります。

『整合終端ではない系』においては、各段での NF の定義があいまいであるため、各段で付加されるノイズを「自乗和平方根」Root Sum Square（RSS）の計算で積み上げていけば答えが出ることが分かりました。

この考え方が理解できることで、これ以降の 2 冊の技術ノートで説明する、アナログ・フロントエンドと、その後段に接続された ADコンバータとによる、ミックスド・シグナル・システム（系）での NF の計算方法が理解できます。

この前編の技術ノートではそのウォーミング・アップとして、 ADC の量子化ノイズの考え方、そして有効ビット分解能 ENOB を探究してみましょう。

なお、今回と次回は、2020 年 10 月 14 日と 15 日に開催された「2020 年アナログ技術セミナー」でご説明した内容とかなりかぶりますので、ご参加された方は復習のつもりで読んでいただければ幸いです。

量子化ノイズとはどんなもの

まずAD変換における量子化ノイズとはどのようなものか考えてみましょう。

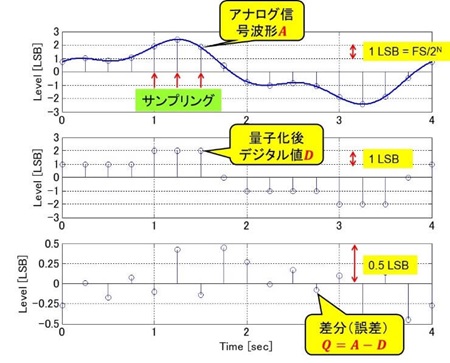
図 2 の一番上は、アナログ信号とそれをサンプリングする動作を示しています。アナログ信号波形𝐴は連続信号です。横軸は時間、縦軸は電圧です。縦軸の 1 ディビジョンは 1 LSB、つまりフルスケール電圧𝐹𝑆を、ビット数𝑁の2^𝑁で割ったものになります。LSBとは Least Significant Bit を略したもので、そのままでは「最下位ビット」と表現されるものですが、AD変換においては「最小分解能」、つまり信号を検出する最小ステップ変化を意味します。

赤の矢印で示したタイミングでサンプリング動作が行われます。このアナログ信号波形𝐴がデジタル値𝐷にサンプリングされると、図 2 の中央の図のように時間と振幅が離散化します。時間はサンプリング周期で離散化し、振幅も ADC の分解能である 1 LSB ステップで離散化し、デジタル値𝐷になります。

縦軸の振幅のみに着目すれば、もともと振幅が連続で変化していたものが、1 LSB を最小とするステップの電圧値に収まる、逆にいうとずれが生じることになります。

つづいて図 2 の一番下をご覧ください。この縦軸は下限が－0.5 LSB、上限が+0.5 LSBになっています。デジタル値𝐷はさきほどお話ししたように、真値𝐴から 1 LSB を最小とするステップの電 圧値にずれることになります。それにより、実際のアナログ信号の大きさ𝐴と離散化されたデジタル値𝐷の差分、

これが真値である𝐴に対しての量子化ノイズ𝑄になります。

本来のアナログ信号の大きさ𝐴が、異なる大きさである離散化されたデジタル値𝐷に変換されるわけですから、その「ずれ」の差分が誤差量𝑄であり、誤差イコール「量子化ノイズ𝑄」と考えることができます。𝑄は真値である𝐴に対しての誤差ですから、 ±0.5 LSB の範囲になります。

量子化ノイズにより得られる SNR を計算する

つづいて SNR（Signal to Noise Ratio; SN 比）を求めるため、量子化ノイズ𝑄の電圧実効値レベルと、ADCフルスケールをフル・ スイングとする信号の電圧実効値レベルを計算してみましょう。

量子化ノイズ電圧実効値を求める

図 3 は量子化ノイズ電圧実効値𝑉_𝑁𝑄を求める考え方です。実効値は Root Mean Square; RMS とも呼ばれます。図 2 で量子化ノイズ 𝑄を示しました。これは±0.5 LSB の範囲ですが、そこで生じる分布は平均的になっています。これを「一様分布」といいます。同図の横軸のスパンはサンプリング周期𝑇_𝑆です。

この図は量子化ノイズ𝑄の分布を表した、ヒストグラム的な電圧分布と考えてください。縦軸は AD 変換による誤差量𝑄を示しています。誤差𝑄がサンプルごとで－LSB/2 から+LSB/2 の間で一様に発生しているイメージです。ここでは－LSB/2 から +LSB/2の間の電圧スパン、つまり ADCの 1ステップを𝑉_𝐿𝑆𝐵としています。

この誤差𝑄を

ただし

と表し、Root Sum Square; RSS の考え方で、まず−𝑇_𝑆/2から+𝑇_𝑆/2まで積分し

この平方根をとると

これが量子化ノイズ電圧実効値𝑉_𝑁𝑄になります。1 ビット最小分解能、1 LSB（=𝑉_𝐿𝑆𝐵）に対して1/√12となるわけです。

入力正弦波波形の電圧実効値を求める

図 4 は ADC フルスケール電圧をピーク・ツー・ピークとする、正弦波波形の実効値𝑉_{𝐹𝑆_𝑟𝑚𝑠}を求める考え方です。ADC の入力電圧スパンをADCフルスケール𝐹𝑆とします。たとえば電源電圧が 3.3V で単電源であれば、ADC 入力は下限が 0V で上限が 3.3V で、それにより ADC フルスケール𝐹𝑆 = 3.3Vとなります。

ここに ADC のフルスケール電圧と等しい正弦波のフル・スイングが加わったとします。なおフルスケール電圧幅を𝐹𝑆と表記していきます。

ピーク電圧は𝑉_𝑃𝐾 = 𝐹𝑆/2、実効値はさらにこの1/√2となり、これにより ADC フルスケール電圧でフル・スイングする正弦波の実効値電圧𝑉_{𝐹𝑆_𝑟𝑚𝑠}が

と得られます。

量子化ノイズにより得られる SNR を求める

さきほどの計算をもとに、量子化ノイズから求められる ADC の 理論的 SNR を計算してみます。ポイントは、前回、前々回の技術ノートで示してきたように、SNR は電圧の自乗値、電力相当比で考えることです。自乗することで1Ωを仮の抵抗値とした電力値に相当します。電圧の比ではありませんので注意してください。

まず SNR の基本的な式は

ここで𝑃_{𝑁𝑂𝐼𝑆𝐸}は量子化ノイズ電力、𝑃_𝑆𝐼𝐺はフルスケール信号電力です。これは dB でない SNR の真値です。

ここで量子化ノイズの影響による理論的 SNR 𝑆𝑁_𝑄を計算してみましょう。さきの二つの実効値を式(6)に代入してみます。

分母は𝑃_{𝑁𝑂𝐼𝑆𝐸}に相当する量子化ノイズ電圧実効値𝑉_𝑁𝑄の自乗値、分子は𝑃_𝑆𝐼𝐺に相当する ADC フルスケール電圧の実効値𝑉_{𝐹𝑆_𝑟𝑚𝑠}の自乗値です。𝑉_𝐿𝑆𝐵は𝑁を ADC のビット数として

これから上記の式(7)は

なお、ここで得られた理論的 SNR 𝑆𝑁_𝑄は、入力信号のピーク・ツー・ピークが ADC フルスケール電圧になるという条件でのSNR なので注意してください。信号レベルが低下すれば実質の SNR は低下することになるわけです。

つづいてこれを dB に変換します。dB にしたものを𝑆𝑁𝑅_{𝑄_𝑑𝐵}とします。電力比なので10 log となり、

さきほど得た𝑆𝑁_𝑄をここに代入します。

これが量子化ノイズから得られる理論的 SNRを dBで表したものになります。

実例の ADC の SNR とノイズ量を計算してみる

実例を示してみましょう。ここでは 12 ビット ADC AD7276 を取り上げてみます。まず AD7276 をご紹介しましょう。この製品は TSOT 8 ピン・パッケージで超小型なADCなのです。

AD7276 12ビットA/Dコンバータ、3MSPS、8ピンMSOP、 6 ピン TSOT パッケージ

https://www.analog.com/jp/ad7276

【概要】

AD7276 は 12 ビット、高速、低消費電力の逐次比較型 ADC です。2.35～3.6V の電圧範囲の単電源で動作し、最大 3MSPS のスループット・レートを実現します。 AD7276には、55MHz を超える入力周波数を処理できる低ノイズ、広帯域幅のトラック／ホールド・アンプが内蔵されています。（後略）

さて AD7276 のデータシートに掲載されている SNR スペック 𝑆𝑁𝑅_{𝑆𝑃𝐸𝐶}は 70dB です。

ADC でノイズが付加されるようすは、図 5 のように、ADC 入力段で生じるノイズと、これまで考えてきた量子化ノイズ𝑄、これらがそれぞれ入力信号に足し算されるイメージとして表すことができます。これを理論的には「加法性; Additive」と表現します。ADC では量子化ノイズ𝑄だけではなく、このように入力段で足し算されるかたちでモデル化されるノイズが、別にもあると理解しておいてください（これはリファレンス電圧のノイズも含まれます）。

まずさきに式(11)として導出した理論的 SNR 𝑆𝑁_{𝑄_𝑑𝐵}を求めてみましょう。さきの式(11)の𝑁に 12 を代入し、計算してみると

 

となります。これはデータシートに記載されている SNR スペッ ク𝑆𝑁𝑅_{𝑆𝑃𝐸𝐶} = 70dBより 4dB良好な数値です。つまり量子化ノイズ以外の要因、入力段で生じるノイズの影響度が大きいということです。

AD7276 の実際のノイズ・レベルを求める

つづいて AD7276 での実際のノイズ実効値レベルを計算してみましょう。この計算はSNRスペック𝑆𝑁𝑅_{𝑆𝑃𝐸𝐶} = 70dBに対して考えるものです。ADC 入力段のノイズ𝑉_{𝑁_𝐼𝑛𝑝𝑢𝑡}と量子化ノイズ電圧実効値𝑉_𝑁𝑄が合わさった、ADC の全入力換算ノイズ電圧実効値𝑉_{𝑁_𝑎𝑑𝑐}のレベル

を求めるものです。

電源電圧 VDDを 3.5Vと仮定して考えます。このとき AD7276ではフルスケール電圧𝐹𝑆も 3.5V になります。この電圧がフル・ス イング入力信号正弦波のピーク・ツー・ピーク電圧に相当します。

ADC のフルスケール電圧𝐹𝑆がピーク・ツー・ピーク電圧となる正弦波の実効値𝑉_{𝐹𝑆_𝑟𝑚𝑠}は、

と計算できます。

ここから AD7276 の実際のノイズ・レベルを求めてみましょう。 SNR の計算式［式(7)を修正］

を用います。SNR スペック𝑆𝑁𝑅𝑆𝑃𝐸𝐶 = 70dB なので、AD7276 の全入力換算ノイズ・レベルの実効値𝑉_{𝑁_𝑎𝑑𝑐}はフルスケール電圧の実効値𝑉_{𝐹𝑆_𝑟𝑚𝑠} = 1.24Vから－70 dB となり、式(13)を変形し

と計算できます。すなわち AD7276 では、ADC 入力段のノイズと量子化ノイズが合算したものとして、入力換算𝑉_{𝑁_𝑎𝑑𝑐}で 392μ Vrms が発生していると計算することができます。

系全体として考える ADC における有効な分解能

ここで「アナログ・フロントエンドも含めた系の SNR に対して、適切な、有効な ADC 分解能は」という課題を考えてみましょう。

信号源抵抗𝑅_𝑆をもつ信号源からの電圧を、アナログ・フロントエンドで増幅、信号処理して ADC に加える、図 6 のような回路 （系）を考えます。アナログ・フロントエンドの意味は最初に示しましたが、ここではとくに信号源を取り込む入力部分から ADC までのアナログ回路を指しています。

アナログ・フロントエンドから ADC に加わるノイズを𝑉_{𝑁_𝑎𝑓𝑒}とします。ADC で付加される、量子化ノイズも含んだ全入力換算ノイズを［先に式(12)で示したように］𝑉_{𝑁_𝑎𝑑𝑐}とします。この 𝑉_{𝑁_𝑎𝑓𝑒}と𝑉_{𝑁_𝑎𝑑𝑐}の合算のノイズが ADC に加わったとき、検出できる、信号本来の最小電圧は？という計算をしてみましょう。

これはつまるところ、この ADC での分解能は何ビットまでが有効かということに相当します。

アナログ・フロントエンドの全ノイズ電圧実効値を得る

アナログ・フロントエンドから ADC に加わる全ノイズ電圧実効値𝑉_{𝑁_𝑎𝑓𝑒}は簡単に算出できます。

まずシミュレーションにおいて LTspice を用いることで、1Hz あたりの出力ノイズ電圧密度スペクトルを、図 7 のように計算することができます。（繰り返しますが）ここで得られたこのようなシミュレーション結果は、1Hz あたりの電圧「密度」になりますので、注意してください。

先に示した𝑉_{𝑁_𝑎𝑓𝑒}は全rmsノイズ量、つまり実効値ですから、このグラフの電圧「密度」を Root Sum Square RSS の考え方で、自 乗値つまり電力密度にして、周波数領域で積分します。でも、その計算は難しそう、面倒と感じるのではないでしょうか。

なお、実機でもアナログ・フロントエンドから ADC に加わる全ノイズ電圧実効値𝑉_{𝑁_𝑎𝑓𝑒}は、ノイズ・メータとかスペクトラム・アナライザを使って実測できます。

LTspice でノイズ電圧実効値𝑉_{𝑁_𝑎𝑓𝑒}を求めるのは簡単です。図 7 のラベルを CTRL + 左クリックでクリックすると、図 8 のように ノイズ電圧実効値𝑉_{𝑁_𝑎𝑓𝑒}、つまりトータル・ノイズを表示できます。この例ではアナログ・フロントエンドのノイズ電圧実効値として𝑉_{𝑁_𝑎𝑓𝑒} = 525μVrms が得られました。

系全体のノイズ電圧実効値を得る

アナログ・フロントエンドと ADC こみこみの、系全体のノイズ電圧実効値𝑉_{𝑁_𝑠𝑦𝑠}を求めてみます。これは「ADC 入力換算で考える系全体で生じるノイズの合算値」です。これも

としてアナログ・フロントエンドのノイズ電圧実効値𝑉_{𝑁_𝑎𝑓𝑒}と ADC の全入力換算ノイズ𝑉_{𝑁_𝑎𝑑𝑐}を Root Sum Square; RSS で計算 します（自乗することで 1Ωを仮の抵抗値とした電力の足し算となります）。

ここまでの例では、アナログ・フロントエンドのノイズ電圧実効値𝑉_{𝑁_𝑎𝑓𝑒}= 525μVrms 、AD7276 の全入力換算ノイズ電圧実効値𝑉_{𝑁_𝑎𝑑𝑐} = 392μVrms なので、

として系全体のノイズ電圧実効値（ADC 入力換算）を計算できます。

ここまでの計算から系全体のシステム SNR を求める

さきの系全体のノイズ電圧実効値𝑉_{𝑁_𝑠𝑦𝑠}と ADC フルスケール電圧の実効値𝑉_{𝐹𝑆_𝑟𝑚𝑠}から、系全体のシステム SNR 𝑆𝑁𝑅_𝑠𝑦𝑠を求めることができます。

さらにシステム SNR から「有効ビット分解能」Effective Number Of Bits; ENOBというものを求めることができます。ENOBはAD 変換システムとして何ビットまで有効かという指標で、量子化ノイズ理論的 SNR 𝑆𝑁𝑅_{𝑄_𝑑𝐵}の式(11)から導出できます。

式(11)では分解能𝑁が与えられていましたが、ここでは𝑁を求める逆算的なイメージです。この式(11)を𝑁について解きます。

この式の𝑆𝑁𝑅_{𝑄_𝑑𝐵}をシステム SNR 𝑆𝑁𝑅_𝑠𝑦𝑠に置き換えることで

もともと分解能𝑁であったものが ENOB として得られます。システム SNR 𝑆𝑁𝑅_𝑠𝑦𝑠の dB 値は

なお確認のため再度示しておきますが、𝑉_{𝐹𝑆_𝑟𝑚𝑠}は ADC フルス ケール電圧実効値、𝑉_{𝑁_𝑠𝑦𝑠}は系全体のノイズ電圧実効値です。

𝑆𝑁𝑅_{𝑄_𝑑𝐵}を求める際は、式(17)の分母は量子化ノイズ電圧𝑉_𝑁𝑄でしたが、これを系全体のノイズ電圧実効値𝑉_{𝑁_𝑠𝑦𝑠}とすることで、システム SNR 𝑆𝑁𝑅_𝑠𝑦𝑠が得られます。そして計算した数値を式 (16)の𝑆𝑁𝑅_𝑠𝑦𝑠に入れることで、ENOB を求めることができます。

ENOB は系全体のノイズ量での ADC 有効ビット数

ENOB は、系全体のノイズ電圧実効値（ADC 入力換算）𝑉_{𝑁_𝑠𝑦𝑠}を既知としたとき、ADC で有効となる分解能のビット数を概算する指標になるわけです。これにより系全体で何ビットまで有効かを計算できます。

なお導出手順からわかるように、系全体のノイズ電圧実効値（ADC 入力換算）𝑉_{𝑁_𝑠𝑦𝑠}が量子化ノイズ電圧𝑉_𝑁𝑄と同じ大きさになるときの分解能𝑁を、ENOBとして計算していることになります。

AD7276 を用いたアナログ・フロントエンドも含 めた系で ENOB を計算してみる

それでは実際に AD7276 とここまで見てきたアナログ・フロントエンドの回路（図 7 にシミュレーション結果を示したもの）とで、どれだけの ENOB が得られるかを計算してみましょう。

先の図 7、図 8 の計算では、AD7276 に加わる系全体のノイズ電圧実効値（ADC 入力換算）𝑉_{𝑁_𝑠𝑦𝑠} = 655μVrmsでした。また AD7276 は、電源電圧 3.5 V だと、フルスケール電圧の実効値 𝑉_{𝐹𝑆_𝑟𝑚𝑠}は 1.24V になります。これにより𝑆𝑁𝑅_𝑠𝑦𝑠は

システム SNR 𝑆𝑁𝑅_𝑠𝑦𝑠 = 65.5dB と計算できます。ここから ENOB を計算してみます。

ENOB は 10.6 ビットと得られます。

ここではアナログ・フロントエンド側のノイズが大きいためということもありますが、12 ビット ADC AD7276 を用いたこの AD 変換の系においては、10.6 ビットの有効ビット分解能 ENOB が実現できるということになります。

アナログ・フロントエンドのノイズ量から ADC を選定する ためにもこの計算は用いられる

なお、アナログ・フロントエンド回路のノイズ𝑉_{𝑁_𝑎𝑓𝑒}だけに着目し ENOB を得て、それにより ADC を選定（ADC のビット数を決定）する計算もできます。これも良く利用される計算方法です。

AD 変換（離散値変換）での折り返しを考慮すると

AD変換では離散値に変換されることによる、折り返しの問題があります。アナログ・フロントエンド側のノイズも図 9 (a)のように折り返されてしまいます。ここまでの議論に関して、この問題をどう取り扱えばよいか考えてみましょう。

一般的な AD 変換におけるサンプリングであれば、よく知られているようにナイキストのサンプリング定理を満足するかたちで、サンプリング周波数𝑓_𝑆の 1/2 以下の帯域（ここを 1st Nyquist Zone と呼びます）を考えます。しかしこれ以上の周波数帯域の信号そしてノイズも、同図のようにサンプリング動作により、この1st Nyquist Zoneに折り返されます（図中ではNyquistをNYQと表記しました）。「1st Nyquist Zone に高域の成分が見えてくる」と言ったほうがよいかもしれません。

そうするとここまで説明してきた、とくに図 7 で示したようなノイズ・スペクトルも、折り返しにより 1st Nyquist Zone に現れるはずと気づくと思います。

しかし実際は同図(b)のように、アナログ・フロントエンドでのアンチエイリアシング・フィルタにより、ノイズ自体も 1st Nyquist Zone内のものが支配的となり、高域のノイズによるノイズ・フロアの上昇は考えなくてもよいケースが多くなります。

それでもハイスピードな ADC などを使用する場合には、注意すべきことでしょう。

なお、1st Nyquist Zone より上の周波数に分布するノイズ、それが 1st Nyquist Zone に折り返された全体量を計算する場合でも、 図8の計算方法をもちいることで𝑉_{𝑁_𝑎𝑓𝑒}を得ることができます。折り返される量も Root Sum Square（RSS）の計算になりますか ら、結局は同じでよいということなんですね。

この話題は次回も取りあげます。

まとめ

量子化ノイズの電圧実効値はLSB/√12になります。そこから量子化ノイズによる理論的 SNRが計算できます。とはいえ ADCの実際の SNR スペックのほうが劣化している場合もあります。これは入力換算として他のノイズの影響があるからです。

また系全体のノイズ電圧実効値（ADC 入力換算）を求めることでシステム SNR が計算でき、システム SNR から「有効ビット分解能」ENOBを求めることができます。それにより AD変換の系として有効となるビット数が得られます。これにより何ビット の ADC が系において適切か把握できるようになります。

次回は

次回はいよいよ、アナログ・フロントエンドと、その後段にADコンバータが接続された、ミックスド・シグナル・システム（系）での NF の計算方法を考え、ADC の分解能をどう考慮すればよいか、そしてフロントエンドと ADC のノイズ配分（フロントエンドの増幅率）をどう最適化すればいいかを、じっくりと解きほどいていきたいと思います。

著者について

石井 聡

1963年千葉県生まれ。1985年第1級無線技術士合格。1986年東京農工大学電気工学科卒業、同年電子機器メーカ入社、長く電子回路設計業務に従事。1994年技術士（電気・電子部門）合格。2002年横浜国立大学大学院博士課程後期（電子情報工学専攻・社会人特別選抜）修了。博士（工学）。2009年アナログ・デバイセズ株式会社入社、現在に至る。2018年中小企業診断士登録。
デジタル回路（FPGAやASIC）からアナログ、高周波回路まで多...