はじめに

今回以降の技術ノートは、2020 年 10 月実施のアナログ技術セミナーでの講演「高いSNRのAD変換システムを実現するテクニックと理論」についての補足となるものです。講演では60分という時間制限のため、このシリーズで説明する内容のほんの一部を講演内に、それ以外はボツにしてしまいました。

この技術ノートそして以降の技術ノートと、またもや何冊になるか分からない、複数冊の技術ノートになりそうですが、「まあ、ここに座って。ゆっくり酒のみながら、お話ししましょうよ」という感じで、じっくり解き明かしてみたいと思います。

2020 年アナログ技術セミナーは初めてのオンライン配信

2020 年 10 月 14 日と15 日に開催された「2020 年アナログ技術セミナー」は、初めてのオンライン配信となりました。

新型コロナ・ウイルスが流行を始めた2020 年の春、社内で「キックオフ・ミーティング」が開催されました。そのときの計画は「2020 年、夏開催。東京会場は◎◎、大阪会場は◎◎」と、会場も決まっていました。それ以降、新型コロナ・ウイルスの流行が拡大し、最初は「開催時期を遅らせて会場で開催」という方向性を模索していました。しかし時が経つにつれ状況が大変厳しくなり、担当者もギリギリまで、難しい判断に迫られていました。そのギリギリの時期に最終判断を行い、「今年はオンライン配信として実行」と決定されました。担当者も「できれば熱気溢れる実会場で開催したい」との強い希望を持っていましたが、残念ながらというか、この環境下に適応するうえでは致し方ない最善の選択肢を選ぶこととなりました。

その一方で、地域的・距離的制限でいままで会場にいらしていただくことが叶わなかった皆様も、オンライン配信によりご聴講いただけたのではという正の側面もあったかと存じます。

そういう私はキックオフ以前から、「今年はADCのノイズについて説明しよう」といろいろ技術検討を進めてきました。その集大成がこの技術ノート・シリーズなのですが、最初の話しのとおり、講演では60 分の時間制限かつ、聴講の皆様の理解／必要性を優先し、エッセンス（必要最小限）のみをプレゼンテーション内容としました。そしてほんの一部をAppendixに掲載、残りは全てボツという、残念な結論だったのでした。

そこで「その全容をこの技術ノートに書き留めよう」と思い立ち、シリーズとして書きだしたものであります。とくに以降で示す ADCを含めたシステムでのノイズ最適化の解説は、手前味噌ではありますが、なかなかこういう解析までした記事はないものかと、ご参考になるものではないかと思っております。

OPアンプのカスケード接続でのノイズ指数は？さらにADCも含んだシステムでのノイズ特性はどう考える？

図 1 は通信システムなどの教科書でよく見る、アンプを3段カスケード接続（従属接続）にしたとき、全体のNF（ノイズ指数／雑音指数）がどうなるかを示すものです。この図のキモは「1段目のアンプがロー・ノイズ特性を決定する支配的要因」ということですが、それをNFという指標で考えるというものです。なお、おのおののアンプの信号源側と負荷側は、50Ωで整合終端した（マッチングした）条件での規定です。

しかし、このNFを少し踏み込んで考えていくと、どうも腹落ち感がないというか、腑に落ちないような壁を感じるのではないかと思います。今回はこのイントロダクションをご説明したいと思います。

ところでNF（ノイズ指数／雑音指数）とは

NF（ノイズ指数／雑音指数）は、名前は聞いたことがあるという方が多いのではないでしょうか。

NFは図 2 のように、入力と出力がある系（この技術ノートでは「複数段の増幅回路システム」を「系」と表現します）において、入力信号の電力レベルとノイズの電力レベルをそれぞれSNR（Signal to Noise Ratio; SN比）として

と表し、出力の信号レベルとノイズ・レベルもSNRとして

と表したとき、その系におけるノイズ特性を

として示すものです。式(3)は真値で答えを得るもので、慣例的に NF = Noise Factorと呼びます。式(4)は dB で答えを得るもの で、慣例的にNF = Noise Figureと呼びます。どちらもNF、また日本語になるとどちらも「ノイズ指数／雑音指数」ですから、「やっかい」な話しです（笑）。

現場では一般的に dB で考える Noise Figure を用いますが、この技術ノートでは理論的しくみを考えていくことから、真値である Noise Factorを用いていきますので、注意してください。

さきのとおり「電力（電圧ならその自乗）」で考えることがポイントです。そのため式(1)、式(2)において、𝑆_𝐼𝑁は系の入力信号電力、𝑆_𝑂𝑈𝑇は系の出力信号電力、𝑁_𝐼𝑁は系の入力ノイズ電力、𝑁_𝑂𝑈𝑇は系の出力ノイズ電力です。

なお残念なお話しですが、このしくみが良く分からないまま書かれている記事、書籍には「電力で考える」ということが記載されていませんのでご注意ください。ひいき目にみれば「当然のこととして、そんな当たり前なことは説明していないんだ」という見方もありますが…。

そういう私も、中堅レベルになるまで「電圧で考えるのか？電力で考えるのか？」の答えを見つけることができませんでした。その糸口は、少し難しい話しになりますが、ノイズが「無相関な信号」であること、またノイズごとの合算は「電力の足し算」つまりRoot Sum Square（RSS）で考えるというところがポイントです。

まず最初の腹落ち感のよくないこと「𝑵_𝑰𝑵はどう考える？」

式としては上記で表されるわけですが、どうも「腹落ち感が良くない」式ではないかと思います。いちばんは「𝑆_𝐼𝑁と𝑆_𝑂𝑈𝑇は信号だから規定／測定できるし、𝑁_𝑂𝑈𝑇は測定すれば何とかなる」。「しかし𝑁_𝐼𝑁はどう考えるんだ？」と思うことではないでしょうか。

つづいて腹落ち感のよくないこと「横軸が周波数？」

さらにもう一つ「腹落ち感が良くない」ことがあります。たとえば低ノイズ RF アンプ、ADL5523のデータシート [1]の Figure 4 から抜粋した図 3 から分かることは、「横軸が周波数」ということです。ここでADL5523を紹介しておきましょう。

ADL5523低ノイズ・アンプ、400MHz～4GHz

https://www.analog.com/jp/adl5523

【概要】

ADL5523 は高性能 GaAs pHEMT の低ノイズ・アンプです。この製品はシングル・ダウンコンバージョンの IF サンプリング・レシーバのアーキテクチャ、あるいはダイレクト・ダウン・コンバージョンのレシーバにおいて、高いゲインと低ノイズ指数を提供します。

ADL5523は、アクティブ・バイアスとDCブロッキング・コンデンサを集積した高レベルな IC で、設計の柔軟性を損なわずに、非常に容易に使うことができます。（後略）

同図中の一番したのプロットがNFを示していますが、説明したように「横軸が周波数」です。SNRそしてNFは信号とノイズの比に関連する指標ですが、なぜ「横軸が周波数なんだ？」と不思議に思うのではないでしょうか。

これは「1Hz あたりのノイズ密度で考える」というのが答えです。実際の NF や素子のノイズ特性を考えるうえでは、（このWEBラボでも何度も出てきましたが）1Hz帯域つまり「ノイズ密度」で考えることが一般的です。

またまた更に腹落ち感のよくないこと「信号の 1Hz あたりの電力密度？」

しかし、でも、そうすると、またさらに「腹落ち」しないところがでてきます。「ホワイト・ノイズは周波数によらず一定密度なので、1Hz あたりのノイズ密度という概念は分かるが、NF計算において信号の 1Hz あたりの電力密度をどう考えるのか？」という疑問が湧いてくるのではないでしょうか。

信号は特定の周波数において帯域が広がったかたちでスペクトルが形成されます。「信号の 1Hz あたりの電力密度？」という疑問も当然でしょう。

ここに NF 計算（算出）のテクニック（1Hz 帯域、電圧密度で考えることを起点として）があるのです。実は「信号の 1Hz あたりの電力密度」は NF の計算では必要がないのです…。

入力ノイズ電力は信号源抵抗のサーマル・ノイズ

まず「𝑁_𝐼𝑁はどう考えるんだ？」の答えは「𝑁_𝐼𝑁は信号源抵抗のサーマル・ノイズ電力を用いる」ということです。信号源は信号電圧源と信号源抵抗から構成されるものであり、信号源抵抗からはサーマル・ノイズが発生します。つまり信号源は「信号電圧源」と「サーマル・ノイズ電圧源」（なお並列で考えれば「サーマル・ノイズ電流源」）から構成され、これらから入力信号のレベルと、入力ノイズのレベル、そこから信号対ノイズの比、SNR（𝑆𝑁_𝐼𝑁）を定義できます。それでは図 2 に示した系を用いて NF を考えていきましょう。

整合終端した系での入力ノイズ電力密度

最初は入出力が整合終端されている状態を考えます。まず系の入力ノイズ電力密度𝑁_𝐼𝑁 [W/Hz]を規定してみます。𝑁_𝐼𝑁は信号源抵抗のサーマル・ノイズ電力です。

図 4 のように信号源抵抗𝑅_𝑆とその抵抗𝑅_𝑆から生じたサーマル・ノイズを消費する負荷抵抗𝑅_𝐿を考えます。ただし𝑅_𝑆 = 𝑅_𝐿（整合終端）とします。高周波システムにおいては、𝑅_𝑆 = 𝑅_𝐿 = 50Ωと考えればより現実的でしょう。ともあれこのとき𝑅_𝐿には

の1Hzあたりの電力密度が生じます。ここで𝑘はボルツマン定数、𝑇は絶対温度です。この𝑃_𝑅𝐿がイコール𝑁_𝐼𝑁になります。整合終端した系においては、負荷抵抗𝑅_𝐿に生じる信号源抵抗からのサーマル・ノイズ電力が𝑁_𝐼𝑁になります。なお𝑁_𝐼𝑁は抵抗𝑅_𝑆,𝑅_𝐿の大きさに依存しません。つまり50Ωでなくてもいいのです。

整合終端しない系での入力ノイズ電圧密度

整合終端をしない、たとえば低周波OPアンプ回路などで考える場合は、信号源抵抗𝑅𝑆の「ノイズ電圧」（これまた図 4 に示してあります）を用います。図 4 のように、負荷抵抗𝑅_𝐿に𝑘𝑇の電力密度が生じるのだとすれば、信号源抵抗𝑅_𝑆の 1Hz あたりのサーマル・ノイズ「電圧」密度は

として計算できます。ここから、抵抗での分圧や信号増幅など、普通に入出力での電圧レベルを計算するのと同じように、式(6)のノイズ電圧が出力に現れる大きさを計算することができます。 NF の計算ではそれを自乗して用いればよいのです。

ここまでで「入力信号の電力レベル𝑆_𝐼𝑁は説明しないの？」と感じるかと思いますが、以降に説明していくように、この変数は NF の計算では使用しません（その変数が消えてしまうため）。

整合終端した系での NF を考える

さて、まずは50Ωで整合終端した系（高周波システムがこの主たる例ですが）を仮定して、NFを考えてみましょう。ここまで信号源抵抗のサーマル・ノイズが、入力信号の𝑆𝑁𝑅の𝑁_𝐼𝑁に相当すると説明しました。𝑁_𝐼𝑁 [W/Hz]は「1Hz 帯域あたりの電力密度」として［式(5)同様で］

これと併せて、信号源から系への入力信号電力𝑆_𝐼𝑁も、数値がいくつとは規定せずに（実はこの変数は消えてしまうため）、「1Hz 帯域あたりの電力密度」としてみます。

ここで式(1)、式(2)、式(3)を利用して、

ここで図 2 のように当然ながら

𝐺は系の電力増幅率です。この式を式(8)に代入すると、

と計算できます。信号電力の変数（𝑆_𝐼𝑁）は消えています。「入力信号電力𝑆_𝐼𝑁を、数値がいくつとは規定せずに」と示したのは、このようにその変数が消えてしまうからなのです。

さらに𝑁_𝑂𝑈𝑇 [W/Hz]は

なお𝑁_𝐴𝑀𝑃は系で生じ、出力に現れるぶんのノイズ電力密度です（ここでは特に、「信号源を除く増幅回路部分」を「系」と表していると考えてください）。信号源抵抗のサーマル・ノイズ電力密度𝑁_𝐼𝑁は信号同様、系の電力増幅率で𝐺倍され、出力に現れるという考え方です。この式を上記の式(10)に代入すると、

これは図 5 のように書き直すことができます。𝑁_𝐴𝑀𝑃/𝐺は系自体から生じるノイズ電力密度を入力換算としたものです。𝑁_𝐴𝑀𝑃/𝐺は、信号源抵抗のサーマル・ノイズ電力密度𝑁_𝐼𝑁と足し算され、系全体の入力換算ノイズ電力密度を形成します。それが系の電力増幅率で𝐺倍され、出力に𝑁_𝑂𝑈𝑇として現れる、というモデルで考えることができます。

ここまでくれば腹落ち感がだいぶ出てくるのではないでしょうか。ここで申し上げたいことは、式(12)を［わざわざ（汗）］再掲してみると

この式から、NF（Noise Factor; F）というのは

・系全体のノイズ電力密度を入力換算で考えたとき

・系から生じたノイズ電力密度を入力換算とした電力（𝑁_𝐴𝑀𝑃/𝐺）が

・どれだけ系全体のノイズ量に加わっているか

ということ、つまり

・信号源のサーマル・ノイズ電力密度に対して

・系で生じ、付加されるノイズ電力密度が

・どれだけ影響を与えるか

を示すものだと分かります。そして「電力で考える」というのは、整合終端した系であるからこそ、この計算が成立するわけですね。

整合終端ではない系での NF を考える

一方でOPアンプなど一般の増幅回路では、整合終端になっていませんから、単純な電力伝達の考え方だけではNFの計算ができません。つまり単純に「電力で考える」というものを適用できません。このような場合はどう計算をするか、つづいて考えてみましょう。

いよいよ本格的に「なんだか腑に落ちない」というあたりに踏み込んできました（笑）。

入力ノイズ電力に相当する大きさ

図 6 のような非反転 OP アンプ増幅回路を考えます。信号源抵抗の大きさを𝑅_𝑆とすると、𝑅_𝑆から生じるサーマル・ノイズのノイズ電圧密度𝑉_{𝑁_𝑅𝑆}は式(6)で与えられます。ここで

信号源抵抗𝑅_𝑆のノイズ電圧密度𝑉_{𝑁_𝑅𝑆}を自乗したもの

がこれまで説明してきた𝑁_𝐼𝑁に相当します。これは負荷抵抗𝑅 = 1Ωに加わる電力𝑃 = 𝑉²_{𝑁_𝑅𝑆}/𝑅 = 𝑉²_{𝑁_𝑅𝑆} として考えるもので、

理論的に考えるアプローチでは、自乗する計算のつじつま合わせのために、このように「𝑅 = 1Ω」として考えることが一般的です。

系で生じ付加される入力換算ノイズを得る

次にOPアンプ自体や帰還抵抗により、系（シツコクてすいませんが、「信号源を除く増幅回路部分」を「系」と表していると考えてください）で生じた複数のノイズ要素（信号源抵抗のサーマル・ノイズ以外）それぞれの入力換算量𝑉_𝑁𝑥を考えます。𝑥 は𝑥番目の要素を意味します。以下の式(14)以降で説明していくように、図 6 のような非反転 OP アンプ増幅回路で生じ、入力換算ノイズを形成する要素は、

・帰還抵抗のサーマル・ノイズ（電圧密度）

・OP アンプ自体の入力換算電圧性ノイズ（電圧密度）

・OP アンプ自体の非反転入力の入力換算電流性ノイズが「信号源抵抗」で電圧降下となったもの（電圧密度）

・OP アンプ自体の反転入力の入力換算電流性ノイズが「帰還抵抗」で電圧降下となったもの（電圧密度）

となります。「系で付加される」分の全ての入力換算ノイズ電圧密度𝑉_{𝑁𝐴𝐷𝐷_𝐼𝑅}は、𝑉_𝑁𝑥それぞれの要素を「電力の足し算」つまり Root Sum Square（RSS）として足し算します。

ここで𝑉_𝑁𝑥は（先にも示しましたが）𝑥番目の要素のノイズ源から生じるノイズ電圧密度です。計算は自乗してそれぞれを足し合わせ（Σ）、ルート（√ ）をとるものです。RSS の考え方の根底は、それぞれのノイズ源がお互いにランダム、つまり相関が無い（無相関な）信号同士だというしくみのうえに立脚して います。結局は式(11)での計算と同じです。𝑉_{𝑁𝐴𝐷𝐷_𝐼𝑅}は以降でも使うので緑色でハイライトしました。

ノイズ・ゲインを考えるとだいぶ話しが厄介だ

これらノイズ源が系の出力に現れる影響度（電圧増幅率）は、「ノイズ・ゲイン𝐴_𝑁𝐺」倍したものになります。

「ノイズ・ゲイン」という用語が出てきましたが、「ノイズ・ゲイン」はこの『回路設計 WEBラボ』でも時々出てきた用語で、

図 7 のように OP アンプの入力換算電圧性ノイズ（赤丸で示した電圧源）が、何倍で出力に現れるかを定義する増幅率＝ ゲイン です。この図の回路構成から分かるとおり、ノイズ・ゲインは非反転増幅回路の信号電圧増幅率に等しくなります。

さて式(14)で「電力の足し算」つまり Root Sum Square（RSS）で足し算した𝑉_{𝑁𝐴𝐷𝐷_𝐼𝑅}を「ノイズ・ゲイン」倍するわけですが、 図 6 の回路は非反転増幅回路なので、回路の電圧信号増幅率𝐴_𝐶𝐿 がそのままノイズ・ゲイン𝐴_𝑁𝐺になります。これならまあ簡単で良いわけですが、回路構成が異なると（たとえば反転増幅回路や加算回路などだと）、ノイズ・ゲイン𝐴_𝑁𝐺は信号電圧増幅率𝐴_𝐶𝐿と一致しないことがあり、単純ではなくなってきます。

これはホントに話しが厄介だ

出力に現れるノイズ電力密度で考えてみましょう。まず信号源抵抗𝑹_𝑺から発生し、出力に現れるノイズ電力密度𝑁_𝑅𝑆は

なお𝑅_𝐿 = 1Ωで考えています。信号源抵抗から生じるノイズ電圧𝑉_{𝑁_𝑅𝑆}（式を追いやすいように青色でハイライトしました）は、 図 8 のように等価的に信号源抵抗に直列に接続されるノイズ電圧源です（図 4 でも示しました）。つまり信号電圧源と直列に接続されていることになり、出力には信号電圧増幅率𝐴_𝐶𝐿倍（電圧比）で現れることになるわけです。そのため式(15)では𝐴_𝐶𝐿が用いられ、また電力増幅率となり自乗になっています（繰り返しますが𝑅_𝐿 = 1Ω）。

出力に現れるノイズ電力密度のうち「系で生じた」ノイズ要素 のみ［式(14)で示したもの］の成分𝑁_𝐴𝑀𝑃は

系で生じた入力換算ノイズが出力に現れる影響度（電圧増幅率）は「ノイズ・ゲイン𝐴_𝑁𝐺倍」したものになります。式(14)で示したように、𝑉_{𝑁𝐴𝐷𝐷_𝐼𝑅}は以降で式を追いやすいように緑色でハイライトしています。

これらにより出力に現れるトータルのノイズ電力密度𝑁_𝑂𝑈𝑇は

式(10)をもちだし、 

これから𝐺 = 𝐴²_𝐶𝐿として、Noise Factor を計算すると、

となり、式(12)と比較しても厄介になることが分かります。ノイズ・ゲイン𝐴_𝑁𝐺と信号電圧増幅率𝐴_𝐶𝐿とが一致しないことがあるからです。非反転増幅回路の場合は、𝐴_𝑁𝐺 = 𝐴_𝐶𝐿になりますから、

と簡単にはなります。

系の出力ノイズを得たほうが簡単だ

さきの式(18)は、入力換算ノイズ電圧密度𝑉_{𝑁𝐴𝐷𝐷_𝐼𝑅}を主体に考えたものです。しかし式(11)の𝑁_𝑂𝑈𝑇、系出力の全ノイズ電圧密度 𝑉_{𝑁𝑂𝑈𝑇_𝑇𝑂𝑇𝐴𝐿}を先に求めて、それを信号電圧増幅率𝐴_𝐶𝐿で割り、さらに信号源抵抗のサーマル・ノイズ電圧密度である𝑉_{𝑁_𝑅𝑆}で割ったほうが、見通しよさそうだと気がつきます。つまり

これは前出の式(10)と同じとなります。式の右辺は自乗していますが、これは「電力で考える」ということです。

また別のアプローチとして、系の出力に着目して（出力換算で）考えることもできます。式自体は式(20)と同じですが

式(20)と式(21)、これらのようにすれば、ノイズ・ゲイン𝐴_𝑁𝐺の影響を考えることなく、NFを計算できることになるわけですね。

こうすれば LTspice でも簡単に NF を評価できる

上記のような考え方を活用すれば、増幅系の NF を LTspice で簡単に評価できることに気がつきます。

図 9 は LT1028[2]で信号電圧増幅率を 100 倍（𝐴_𝐶𝐿 = 100）にして、信号源抵抗𝑅_𝑆を10Ω、1kΩ、100kΩと変化させた、LTspice のシミュレーション回路図です。LT1028は超低ノイズの OP アンプで、簡単にご紹介しますと、

LT1028 超低ノイズ・高精度・高速オペアンプ

https://www.analog.com/jp/lt1028

【概要】

LT1028(利得－1 で安定)/LT1128(利得+1 で安定)では、0.85nV/√Hz(1kHz)および1.0nV/√Hz(10Hz)など新しいノイズ性能の規格が得られます。この超低ノイズとともに優れた高速仕様(利得・帯域幅積が LT1028 では75MHz、 LT1128 では 20MHz)、無歪み出力、および高精度パラメータ(0.1µV/°Cのドリフト、10µVのオフセット電圧、 30,000,000 の電圧利得)が得られます。LT1028/LT1128 の入力段はほぼ 1mA のコレクタ電流動作によって低電圧ノイズを達成していますが、入力バイアス電流はわずか 25nAです。（後略）

SPICE シミュレーションで各素子の影響度は、出力換算で結果が表示されます。図中の信号源抵抗に相当する RS も出力換算として、LTspice ではV(rs)という関数で「出力換算ノイズ電圧密度」が得られます。

そこで式(21)を用いてシミュレーション結果を

V(onoise)**2/(V(rs)**2)

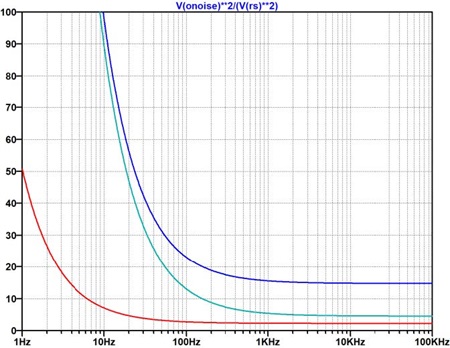
と計算させることにより、簡単に Noise Factor を得ることができます。「**2」という演算は自乗するという意味です。シミュレーション結果を図 10 に示します。

青のプロットは信号源抵抗が100Ω、赤色は1kΩ、空色は 10kΩです。100Hz から下のあたりで NFが劣化（上昇）しているのは、 1/fノイズの影響です。また信号源抵抗の値を変えていくと、NF が変化していることが分かります。

これは信号源抵抗が小さいと、信号源抵抗のサーマル・ノイズ電力密度𝑁_𝐼𝑁［式(6)、式(13)で示した、信号源抵抗のサーマル・ノイズ電圧密度𝑉_{𝑁_𝑅𝑆}の自乗値］が小さくなることが理由です。

しかし10kΩにおいては、また NF が上昇しています。これは LT1028 の入力換算電流性ノイズ（電流密度 1pA/√Hz）が 10kΩに流れ、電圧降下になったもの（電圧密度で10nV/√Hz）が、アンプ入力で発生し、付加ノイズとして影響が出てくることが理由です。10kΩの信号源抵抗から生じるサーマル・ノイズ電圧密度は 12.9 nV/√Hzになりますから、それとほぼ同じ電圧降下になるわけです。

NF は信号源抵抗に大きく依存する

一般論としてここで注目すべきことは、「NF は信号源抵抗に大きく依存する」ということです。しつこくて申し訳ありませんが

また

ここで信号源抵抗𝑅_𝑆が大きくなれば、それに応じて NF も向上（低下）してくることが分かります。つまり信号源抵抗が大きくなれば「見かけ上（というのが正しいのか分かりませんが…）、 NF は向上（低下）する」のですね。

思い出してみると昔々、とある JFET のデータシートに信号源抵抗と NFのグラフが掲載されていたのを見たことがあります。そこにはまさしく信号源抵抗を大きくすると、NFが低下してくる特性がプロットされていました。この説明と同じなわけですね。

電流性ノイズの小さい CMOS OP アンプでシミュレーションしてみる

さきの LT1028は電流性ノイズ密度が 1pA/√Hzで、10kΩの信号源抵抗ではその影響度が見えてくるというものでした。そこでここでは、電流性ノイズ密度が低い AD8616 [3]という CMOS OP アンプを使って、あらためてシミュレーションしてみます。 AD8616 は私もよく使う OP アンプで、ご紹介しておきますと、

AD8616 オペアンプ、デュアル、高精度、20MHz帯域、レール to レール、CMOS

https://www.analog.com/jp/ad8616

【概要】

AD8615／AD8616／AD8618 はそれぞれシングル／デュアル／クワッドのレールtoレール入力／出力の単電源オペアンプで、非常に低いオフセット電圧、広い信号帯域幅および低い入力電圧、電流ノイズを特長としています。これらのアンプは特許収得済みのトリミング技術を用いており、レーザ・トリミングを使わずに並外れた高精度を実現しています。全てのアンプは、+2.7V～+5V の単電源での動作が完全仕様規定されています。（後略）

AD8616 は電流性ノイズ密度が 0.05pA/√Hzなので、10kΩで生じる電圧降下も 0.5nV/√Hzで、影響度がかなり低下します。さきに示したように、10kΩの信号源抵抗から生じるサーマル・ノイズ電圧密度は 12.9 nV/√Hz なので桁が全く違います。

シミュレーション回路は、図 9 から OP アンプを交換したものです。LTspice に入っているモデルは AD8618 しかありませんでし たので、AD8618 を用いました。AD8618 は 4 個入りのアンプであり、中身は AD8616 と一緒です。シミュレーション結果を図 11 に示します。式(12)や式(13)からの予想通りの結果になっていることが分かります。

まとめと次回予告

NF について、50Ωで整合終端したケースでの考え方と、整合していない OPアンプ増幅回路のケースでの考え方をそれぞれ説明しました。「なんだか腑に落ちない」NF の計算ですが、整合終端したケースであれば複雑ではないことから、ご理解いただけたのではと思います。

一方で OPアンプ増幅回路など整合していないケースでは、なんだか七面倒な話しかつ、どうも「腹落ち感のない」…、「腑に落ちない」話しであることが（「そういう話しだ」というだけでも結構ですが）お分かりいただけたものかと思います。

また NFは信号源抵抗の大きさに依存することも注意点で、これもさらに NF自体を「腹落ち感のない」…、「腑に落ちない」ものにしていく要因だといえるのではないでしょうか。

整合終端ではないケースの NFについて、今回は非反転増幅回路で考えてきました。次回は系（ホント、シツコクてすいません （涙）。「信号源を除く増幅回路部分」を「系」と表しています）の入力抵抗が低くなる反転増幅回路で、NF がどうなるかをまず考えていきます。つづいて図 1 で示した、カスケード接続（従属接続）にしたときの系全体の NF 計算方法について、50Ωで整合終端したケースと、OP アンプ回路など整合していないケースについて、それぞれどう考えればよいかをお話ししていきたいと思います。

それにより、さらに以降の技術ノートで説明する、アナログ・フロントエンドとその後段に AD コンバータが接続された、系全体での NF をどう考えるかの下地を作ってみましょう。