要約
Nonideal cable dispersive effects can affect system performance. This application note discusses the two main loss effects related to cables (skin-effect and dielectric losses), and presents a simple method of modeling the cable for use in standard SPICE simulators.
A similar version of this article appears on EDN, July 30, 2012.
Introduction
Cables are used in many high-frequency board designs and can become a critical element in the signal path. This is especially true for signals that exceed 500MHz. If not modeled as part of that system, cables can lead to unexpected system performance degradation and to costly time delays in debugging and corrections. Even with this understood, cables are notoriously difficult to model correctly. Using a simple transmission line model may not effectively model this element because it is difficult to model a cable both in the frequency and the time domains.
Cable nonideal dispersive effects can affect system performance. These cable effects are seen¹ on drivers, buffers, and comparators. In the driver or buffer, the low-frequency dribble up (Figure 1) primarily degrades propagation delay versus pulse-width dispersion; it also degrades minimum pulse time and rise time. In the comparator, the low-frequency dribble up primarily degrades delay versus pulse width and propagation delay versus overdrive; it also degrades the minimum pulse width. This application note will discuss the two main loss effects related to cables: the skin effect and dielectric losses. We will then present a simple method of modeling the cable for use in standard SPICE simulators.

Figure 1. Example of cable loss effects (simulated results from Figure 3 below).
Why Model a Cable?
As frequencies start to exceed 500MHz, the cable starts to noticeably impact the bandwidth of the signal path and begins to degrade this path in many ways. To understand the effects of cables at all frequencies, the cable needs to be modeled. However, based on that model, more intelligent decisions can be made about the type of cable to be used. Moreover, the parameters of interest that are being degraded in the signal path can then be understood.
Cable Losses
There are two main loss mechanisms with cables: skin-effect and dielectric losses.
Skin-Effect Losses
At high frequencies, the signal tends to propagate along the surface of the conductor. This is known as skin effect. (Note that this application note will not rigorously discuss skin-effect losses.) The skin depth, δ, is defined as:

Where ω is the frequency in radian per second; µ is the conductor's permeability in H (Henries per meter); and σ is the conductor's conductivity in S (Siemens per meter).
Equation 1 shows that the skin depth decreases with the square root of the frequency. Alternatively, since the lower the skin depth the higher the resistance per unit length, then the resistance per unit length, RL, increases with the square root of frequency.
Therefore, RL = 1/Wδσ, where W is the conductor's cross-sectional width (for a circular wire, W = 2πr). Rewriting:

Dielectric Loss
The dielectric constant of insulators has an imaginary component. The dielectric constant, ε, is defined as ε = ε' + jε'' = ε'(1 + jtanδ), where ε' is the real component of the dielectric constant; and tand is the loss tangent or dissipation factor of the dielectric. The dielectric constant affects the capacitance and the Cl (capacitance per unit length) will change to Cl(1 + jtanδ).
Total Cable Loss
By including the skin-effect and dielectric losses in the model, an ideal cable model (per unit length) can be now modified to include those losses (Figure 2). Here Ll, Rl, and Cl are the per unit length for inductance, resistance, and capacitance, respectively.

Figure 2. Ideal cable representation.
The propagation constant is defined as jk = √ZY, where Z is the distributed series impedance and Y is the distributed parallel admittance.
From Figure 2 we see:

Using a Taylor-Expansion approximation:

Further simplifying:

Where Zo is the cable's characteristic impedance; εr is the relative dielectric constant; and c is the speed of light.
We are actually seeking the cable gain, H(ƒ). Therefore, H(ƒ) = e-jkl, where l is the length of the line.
Using the findings above:

Where:

Therefore, skin-effect losses (α1) dominate at lower frequencies and dielectric losses (α2) dominate at higher frequencies.
Note that in real-world cables H(ƒ) varies somewhat from the approximations given above. However, this model is accurate enough for most automated-test-equipment (ATE) work, where the attenuation increases to 6dB at the most.
We will be using Equations 6, 7, and 8 later to model the cable.
SPICE Approximations
Unfortunately, H(ƒ) cannot be modeled well in the time-domain SPICE and electromagnetic (EM) simulators. Typical EM simulators generate a lumped transmission line approximation. The lumps must be small enough to look like a transmission line at the frequency of interest, and the lumped elements must vary with frequency. This typically generates a very big model for longer lines.
S-parameter data from manufacturers can also be used to model the frequency response of the cable. But S-parameters only model the AC response and not the transient response. S-parameter extraction requires very accurate equipment, setups, and calibrations, and is not always readily available. You also need to have a different set of S-parameters for each cable length, which again is difficult to obtain.
Alternatively, H(ƒ) can be approximated by a multiple-pole/zero-fit network. This pole/zero network models both the AC and transient performance. The pole/zero fits the magnitude very well, but the phase-fit error can be significant. Because the phase is linear with frequency, it appears as an ideal transmission line and can, thus, be eliminated. A -3dB pole/zero fit matched an EM simulator within 3 degrees phase error up to the -3dB point.
There are two notable shortcomings to a pole/zero network model:
- The pole/zero network does not include the ideal phase-dependent part of H(ƒ)—the part that varies linearly with frequency. This is usually not needed, since the ideal phase lag looks like an ideal transmission line. If the phase of H(ƒ) is needed, add an ideal transmission line in series with the pole/zero network.
- The pole/zero network assumes matched characteristic impedance over all frequencies. Ll changes with frequency. For reasonable losses (less than 6dB), the change in Ll is insignificant. For larger losses, the pole/zero network would err.
The Model
The model, shown in Figure 3, consists of six cells. Five of these cells are configured with a pole and a zero response. The sixth cell has just a pole response. Thus, the entire model is made up of six poles and five zeroes. Six poles and five zeroes were chosen to give a "good" fit. There is no reason why you could not reduce or increase the number of poles and zeroes. The trade-off will be accuracy. The "dribble up" plot shown in Figure 1 was simulated from Figure 3.
Figure 3 is a model of 30 meters, or 100 ft of RG58U cable. The values of the components for this model will be developed later and will be shown to match very closely to the measured data. The advantages of the model in Figure 3 are its simplicity, its high-level abstraction that allows for fast simulations, and its accuracy. You can also run both AC and transient analysis on it. Figure 4 shows the basic representations of the pole/zero and pole configurations used in the Figure 3 model.

Figure 3. Final model for 100 feet of RG58U cable, modeled with a 6-pole/5-zero approach.

Figure 4. Representation of the pole/zero and pole, cascaded together in Figure 3.
Pole/Zero Derivation (based on Figure 4):
VOUT/VIN = (1 + R2 × C1 × S)/(1 + (R1 + R2) × C1 × S)
Pole = 1/(2 × π × (R1 + R2) × C1), Zero = 1/(2 × π × R2 × C1)
Pole Derivation (based on Figure 4)
VOUT/VIN = 1/(1 + R1 × C1 × S)
Pole = 1/(2 × π × R1 × C1)
Figure 5 shows the conceptual and graphical representation of how the pole/zero concept is fitted to the real response.
Note that we are modeling a 30m or 100ft. RG58U cable. As will be seen by the GNUPLOT-generated plot, the fit is very good all the way out to better than -30dB. In general, it is more accurate to model cables out to -6dB.

Figure 5. Graphical representation shows how the 6-pole/5-zero model fits the real response.
Derivation of the Model
Appendix A is a GNUPLOT file that uses the physical constants of the cable. In this example, we use the RG58U cable and mathematically define the cable response utilizing Equations 6, 7, and 8 above. It then plots this response. The GNUPLOT file mathematically models the pole/zero and pole responses, as shown in Figure 3, and then calculates the values of the Rs and Cs. The calculation involves the use of the GNUPLOT "FIT" function. This function will do a least-square fit to find the poles and the zeroes. It will plot this calculated response, or "fit," and overlay this on the cable's response, as defined by the physical parameters. Appendix A shows that the real response of the cable, defined by the cable's physical properties, is accurately matched by the least-square fit, based on a 6 pole/5 zero fit.
Finally the GNUPLOT file calculates the R and C values for Figure 3, which then becomes the model and can be simulated by any SPICE simulator. Finally, we overlay the real cable response, the least-square approximation, and then the simulated plot from the model. It will be shown that all three plots agree very closely and, hence, confirm the model.
Figures 6 and 7 are SPICE simulations from the derived model of the 100ft. RG58U cable.
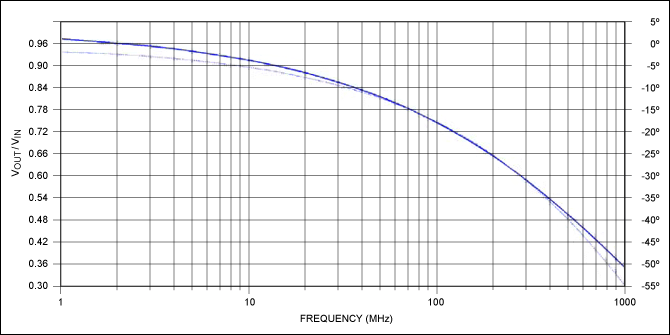
Figure 6. Frequency response of Figure 3 (our model). SPICE response of the schematic model.

Figure 7. GNUPLOT-generated plot of the physical model and calculated pole/zero model.

Figure 8. AC input impedance plot of Figure 3 (our model); SPICE response of the schematic model.
Procedure to Create the Model
- Obtain manufacturer's data for the physical characteristics of the cable:
- Magnetic permeability (u = 1.2e6H/m)
- Speed of light (c = 300me6 mps)
- Conductivity of the signal wire (copper = sigma = 58.6e6 spm)
- Characteristic impedance of the cable (for RG58U = 50Ω)
- Relative dielectric constant for the insulator material (for RG58U, er = 2.3 for solid polyethylene)
- Loss tangent of the insulator (for RG58U, tand = 0.00035)
- Signal cable width (for RG58U = 4.5e × 10-4 m = 0.00045m)
- Cable length: this will be the only parameter that will vary and can be passed.
- Run the GNUPLOT program in Appendix A.
- Create the first estimates for wp1 to wp6 and wz1 to wz5 (poles and zeroes). The program in Appendix A already has these first estimates.
- If the error as shown in Appendix B is greater than a few percent, insert the calculated poles and zeros back into the GNUPLOT program and run and reiterate until the error is below a few %. If you do not do this and have large errors in the calculated "fit," you will get errors in the calculations of the Rs and Cs for the final model.
- Adjust the Rs and Cs as calculated in the GNUPLOT program in Appendix A and printed in Appendix B into the Figure 3 schematic.
- Run an AC sim for Figure 3. Review that the frequency response matches the GNUPLOT responses, as shown in Figures 6 and 7. If they agree, you are done.
- You can then run various lengths of the cable to create new models for these different lengths. The schematic becomes the model and will show both transient and frequency characteristics of the cable.
Summary
This application note showed a simple approach to modeling a signal cable by obtaining just the physical data for that cable. This process extends to all cables. A cable signal's characteristics are defined by its physical construction and the materials used. The more normal approach is to obtain S-parameter sweeps or create distributed RLC elements to model the cable. These do have their place. S-parameters are limited to AC analysis only and must be redone for every cable and length of that cable. The major limitation of S-parameters is their lack of transient information. S-parameters can be hard to retrieve. Either the manufacturer supplies these parameters or you must have expensive equipment to extract these parameters and perform methodical calibration routines. Distributed models allow for AC and transient modeling, but they are difficult to obtain. Distributed models to obtain an accurate model can also be quite large and slow down SPICE simulations tremendously.
The greatest advantage of the model presented here is that none of the above restrictions apply. Rather, you get or determine:
- A simple modeling interface
- Need only obtain the physical information of the cable.
- The pole/zero fit provides a very accurate model of the loss response.
- The model parameters for the poles and zeros are easily calculated to create the schematic.
- The only parameter in this model is the length of the cable.
- It is easy to compose a library of cables from the physical parameters and pass these calculated Rs and Cs to a circuit that remains the same.
- Quick, easy "what if analysis" right at your bench
- Can easily be ported to MATLAB® for greater GUI flexibility.
This model does have its limitations, as discussed. Many versions of cable models can be more accurate, but they also can be very complex and unwieldy. This approach gives a very simple method for modeling a cable, and the method has very good accuracy over at least a -6dB loss. While it models well past this loss, you would have to account for impedance and phase differences if these impact the design.
Appendix A. GNUPLOT File
# GNUPLOT File that: #1) Calculates the frequency response after calculating the skin effect and dielectric effects, using only the physical parameters of the cable. #2) It then plots the frequency response caused by these physical parameters and stores that information in a file called droop.csv. #3) We then define a pole/zero and pole response, based on frequency, the pole, and the zero. #4) We cascade five pole/zeroes and one pole. #5) We then calculate the six poles (wp1 to wp6) and the five zeroes (wz1 to wz2) using the GNUPLOT "Fit" function. #6) We then calculate a SPICE-equivalent schematic with Rs and Cs defined by the poles and zeroes. #7) We plot the calculated physical response and overlay that with the mathematically calculated fit, based on a 6 pole/5 pole fit. #8) The Rs and Cs are passed onto a SPICE high-level schematic, and this models the cable. This schematic can then run AC or transient simulations. #9) Lastly, we run the SPICE model and obtain the response and compare this to the physical response and the mathematical response. All three responses must lie on top of one another to ensure a good model fit. # Frequencies of interest fmin = 1e+6 # minimum frequency (Hz) fmax = 1e9 # maximum frequency (Hz) # Physical constants u=1.26e-6 # magnetic permeability (H/m) c=300e+6 # speed of light (m/s) # Line-specific constants for cable sigma=58e+6 # copper conductivity (S/m) z0=50 # characteristic impedance (Ohms) er=2.3 # relative dielectric constant RG58U cable (solid Polyethylene) tand=0.00035 # loss tangent/dissipation factor (polyethylene) w=2*pi*4.5*10-4 # cross-sectional cable width (m) #l is line length (m) l=30 # Attenuation constants a1=(l/(2*w*z0))*sqrt(pi*u/sigma) # skin effect. Same as Equation 6. a2=(l*pi*tand*sqrt(er))/c # Dielectric Effect. Same as Equation 7. print "a1=", a1 print "a2=", a2 # Plot the loss including skin and dielectric effects plot [f=fmin:fmax] exp(-a1*sqrt(f)-a2*f) # Plotting Equation 8. set terminal table set logscale x set output 'droop.csv' set title "Cable Response via Physical Descripton vs Mathematical Fit" set xlabel "Frequency"; set ylabel "Amplitude (v)" set xrange [1e6:1e9] #Setup for plotting to terminal replot set terminal x11 set output fscale=1e9 # Define pole zero and pole equations # pole/zero pz(x,p,z)=(1+((2*pi*x)/(2*pi*z))**2)/(1+((2*pi*x)/(2*pi*p))**2) # pole p(x,p)=1/(1+((2*pi*x)/(2*pi*p))**2) # Eq2 # 6-pole fit - cascading 6 pole/zero and one pole utilizing pz(x.p.z) and p(x,p). Where x is the frequency. f6(x)=sqrt(pz(x,wp1,wz1)*pz(x,wp2,wz2)*pz(x,wp3,wz3)*pz(x,wp4,wz4)*pz(x,wp5,wz5)*p(x,wp6)) # Define our initial estimates wp1=7e-3*fscale; wz1=8e-3*fscale; wp2=6e-2*fscale; wz2=7e-2*fscale; wp3=2.5e-1*fscale; wz3=3.5e-1*fscale; wp4=.25*fscale; wz4=0.1*fscale; wp5=.5*fscale; wz5=1*fscale; wp6=12*fscale # Call GNUPLOT's "fit" function to calculate poles and zeroes by least square method fit f6(x) 'droop.csv' using (10**$1):2 via wp1, wz1, wp2, wz2, wp3, wz3, wp4, wz4, wp5, wz5, wp6 #Overlay the Cable Characteristics vs the Mathematical Fit. plot 'droop.csv' using (10**$1):2, f6(x) #Calculate Rs and Cs for pole/zero schematic normalized for a 50 ohm characteristic impedance. #Pole Zero1 r1= 50*((wz1/wp1)-1);c1=1/(2*pi*50*wz1) #Pole Zero2 r2= 50*((wz2/wp2)-1);c2=1/(2*pi*50*wz2) #Pole Zero3 r3= 50*((wz3/wp3)-1);c3=1/(2*pi*50*wz3) #Pole Zero4 r4= 50*((wz4/wp4)-1);c4=1/(2*pi*50*wz4) #Pole Zero1 r5= 50*((wz5/wp5)-1);c5=1/(2*pi*50*wz5) #Last Pole c6=1/(2*pi*50*wp6) print "r1=",r1;print "c1=",c1 print "r2=",r2;print "c2=",c2 print "r3=",r3;print "c3=",c3 print "r4=",r4;print "c4=",c4 print "r5=",r5;print "c5=",c5 print "c6=",c6 pause -1 'Hit return to continue'
Appendix B. Output Log of GNUPLOT File Run in Appendix A
After 480 iterations the fit converged. Final sum of squares of residuals: 5.84016e-06 Rel. change during last iteration: -4.6111e-06 Degrees of freedom (ndf): 89 rms of residuals (stdfit) = sqrt(WSSR/ndf) : 0.000256164 Variance of residuals (reduced chisquare) = WSSR/ndf: 6.56198e-08 Final set of parameters Asymptotic Standard Error ======================= ========================== wp1 = 646510 +/- 1.679e+04 (2.596%) wz1 = 670473 +/- 1.775e+04 (2.647%) wp2 = 5.03764e+06 +/- 1.362e+05 (2.703%) wz2 = 5.27773e+06 +/- 1.462e+05 (2.77%) wp3 = 8.39629e+07 +/- 1.863e+06 (2.219%) wz3 = 9.95475e+07 +/- 2.375e+06 (2.385%) wp4 = 2.22295e+07 +/- 5.627e+05 (2.531%) wz4 = 2.43028e+07 +/- 6.414e+05 (2.639%) wp5 = 2.8391e+08 +/- 4.841e+06 (1.705%) wz5 = 3.99073e+08 +/- 7.35e+06 (1.842%) wp6 = 9.06085e+08 +/- 6.952e+06 (0.7673%) r1=1.85319306240795 c1=4.74754480502755e-09 r2=2.38294740571777 c2=6.03118500463386e-10 r3=9.28066392395646 c3=3.19756688710695e-11 r4=4.66322485796558 c4=1.30976817734003e-10 r5=20.2815653367384 c5=7.97623211328647e-12 c6=3.51302554048115e-12 Hit return to continue




















