傾斜測定の一般的なアプリケーション
アナログ・デバイセズは、加速度センサーとジャイロスコープを集積したシングルチップ製品を提供しています。本稿では、この種の製品のことをコンボ品と呼ぶことにします。本稿のテーマは、そのコンボ品による傾斜測定の精度はどうすれば高められるのかということです。例えば、乗用車では、電動パーキング・ブレーキ(EPB:Electric Park Brakes)という機能が使われています。これを使用すれば、平坦な路面だけではなく、傾斜のある路面でも停止することができます。この EPB 機能は、1軸または 2 軸の加速度センサーで傾斜を測定することによって実現されます。一般に、EPB では、制御ユニットの専用モジュールに、低 g (小さい g の測定)に対応する x 軸/y 軸または z 軸の加速度センサーが配置されます。近年は、横滑り防止装置(ESC: Electronic StabilityControl)が、より多くの車両に採用されるようになりました。というのも、多くの国では、車両の横滑りや横転を防止するために、ESC の装備が法律によって義務づけられるようになったからです。この ESC は、低 g の加速度センサーとジャイロスコープをシングルチップに集積したコンボ品を使用して実現されるケースが増えています。コンボ品によって傾斜測定を行うことで、スタンドアロン型の EPB モジュールを車両に備え付ける必要はなくなり、車両のコストを大幅に削減することができます。ただし、ESC に一般的に用いられるコンボ品は、傾斜の検出用に最適化されているわけではありません。そのため、コンボ品による傾斜測定では、必要な精度が得られないことがあります。コンボ品は x/y 軸または x/y/z軸に対応します。傾斜測定には、一般的には x 軸が使用されます。EPB モジュールで使用される低 g の従来型加速度センサーの場合、エンジン・ルーム内で垂直に配置されて Z 軸が使われることがあります。精度を高めるには、検出軸を重力と垂直に配置する必要があります。これについては後述します。

図 1. x 軸加速度センサーとz 軸加速度センサーの使用方法
車両の傾斜測定では、精度についての評価が非常に重要な意味を持ちます。ある車両が完全に平らな地面に駐車しているケースを考えます。その場合、加速度センサーによって得られる角度は 0° になるはずです。一方、傾斜面に駐車している場合には、ブレーキ・システムが正しく作動するように、傾斜を正確に検出する必要があります。

以下の式をご覧ください。

ここで、AOUT は加速度センサーの出力(単位は g)、Θは傾斜面の傾き(単位は °)です。これを変形すると以下の式が得られます。


sinΘ は非線形の関数なので、AOUT と Θ の関係も非線形になります。線形性は 0° 付近で最も高くなります。それは測定精度も最も高くなるということを意味します。逆に、Θ が 0° からだんだん大きくなるにつれて、測定精度は低下します。路面の傾斜角は 0° に近いので、検出軸は重力と垂直に配置する必要があります。
車両の傾斜測定を前提とする場合、あらゆる傾斜角に対応するシステムを開発しようとする必要はありません。現実の路面の場合、傾斜角が 30° を超えることはめったにないからです。±30° の範囲だけを対象とし、精度にかかわる要因について解析すれば十分でしょう。
システム・レベルの測定精度には、以下に示す要因が寄与します。
- 感度誤差と初期絶対オフセット
- 非線形性
- 初期絶対オフセットからの総変化量
- ノイズ
感度誤差と初期絶対オフセット
感度誤差
ここで言う加速度センサーの感度とは、センサーの伝達関数(加速度センサーにおける入力と出力の関係)において、+1 g と -1 g の間に現れる傾きのことです。また、感度誤差とは、各デバイスに生じる感度のばらつきのことです。ある加速度センサーの場合、感度は最大で 3%程度になります。

初期絶対オフセット
初期絶対オフセットとは、25°C程度(例えば、25±5°C)の条件下で、製造直後のモジュールにおいて測定されたオフセットのことです。特定の品種の初期絶対オフセットは、多数のデバイスを対象として測定されたオフセット値の標準偏差を使って定義されます。
2 点キャリブレーション
傾斜測定における主な誤差要因は、オフセット誤差と感度誤差です。これら 2 つの誤差は、検出結果に許容できないレベルの誤差をもたらす可能性があります。オフセット誤差と感度誤差を除去するには、加速度の出力を対象としてキャリブレーションを実施する必要があります。傾斜測定の場合、オフセットと感度については 1 回のキャリブレーションが実施されます。オフセット誤差と感度誤差に着目すると、加速度センサーの入力と出力の間には次の関係があります。

ここで、AOFFSET は、オフセット誤差(単位は g)、Gainは加速度センサーのゲイン(理想的な値は 1)、AACTUALは、加速度センサーに加わる実際の加速度(単位は g)です。
基本的なキャリブレーション方法としては 2 つの手法を挙げることができます。1 つは 1 点キャリブレーションです。加速度センサーに 0 g のフィールドを適用して出力を測定します。1 点キャリブレーションではオフセット誤差を補正します。ゲイン誤差は補正できません。0 g のフィールドで測定した出力を、実際の出力値から差し引くことにより、オフセット誤差を除去できます。簡単に実施可能なキャリブレーション方法ですが、感度誤差を除去できないので、高い精度が必要な場合には適していません。もう 1 つの方法は、1 g 反転キャリブレーションです。これは +1 g と -1 g を使用する 2 点キャリブレーションです。+1 g と -1 g の各フィールドで加速度出力を測定します。その結果は、以下のような式で表されます。

ここで、A+1 g と A-1 g は、それぞれ +1 g と -1 g に対応する測定値です。AOFFSET はオフセットを表します。単位はいずれも g です。
これらの結果から、以下のようにしてオフセットとゲインを求めることができます。

この 1 回のキャリブレーションを実施した後、次の式によって実際の加速度を求めることができます。

AOUT の単位は g です。キャリブレーションを実施する度に、オフセット誤差と感度誤差が除去されます。
非線形性
加速度センサーの非線形性とは、線形の入力に対して線形に出力される理想的な加速度 AFIT に対する実測値 AMEAの最大偏差のことです。実測値のデータには、加速度センサーのフルスケール範囲に対応する結果が含まれている必要があります。非線形性は、Max(|AMEA - AFIT|) で求められます。

ここで、AMEA は、ある入力加速度 gn における出力加速度の測定値、AFIT は gn における出力加速度の予測値です。
ほとんどの加速度センサーまたはコンボ品は、所定の入力範囲(例えば、30 mg ± 2 g の範囲)において非線形性を示します。傾斜測定の場合、入力傾斜角は ±30° の範囲内だと考えられます。そのため、出力加速度は ±500mg(±1 g × sin 30°)の範囲内になります。したがって、この範囲の非線形性について再評価する必要があります。非線形性は、入力範囲の全体に対して線形に現れるわけではありません。そのため、この誤差要因について正確かつ定量的に評価を行うことは困難です。データシートに、±2 g の入力範囲に対して非線形性が 30 mg と記載されている製品があったとします。その場合、非線形性の保証値としては安全側に振りすぎていると考えられます。±500 mg の範囲に対する誤差の計算においては、10mg を使用する方が理にかなっているでしょう。
初期絶対オフセットからの総変化量
初期絶対オフセットからの総変化量とは、温度、ストレス、経年劣化の影響によって生じるオフセットの最大偏差のことです。この偏差は、対象となるデバイスにおける初期絶対オフセットの値を基準として測定されます。これは、精度(つまりはトータルの誤差)に対して最も大きな影響を及ぼす要因になります。
温度、ストレス、経年劣化といったあらゆる要因の中で、オフセットの総変化量に最も大きな影響を及ぼすのは温度です。一般に、変化量の温度依存性を表すグラフは 2次曲線(通常は回転放物線)になります。この誤差要因を除去するには、システム・レベルの 3 点キャリブレーションが必要になります。任意のデバイスに対し、温度による出力の変化量は、以下に示す手順によって校正することができます。
ステップ 1:
デバイスの出力応答は、オフセットの分だけずれています。そのオフセットの値を Δ N0 と表すことにします。温度に関するキャリブレーションの最初のステップでは、周囲温度におけるオフセットである Δ N0 を除去します。


ステップ 2:
次に、高温環境下でデバイスの試験を行います。それによって新たに得られた情報を使用し、オフセットを補正するための 1 次式を生成します。


ステップ 3:
残りのオフセットを補正するために、既存の式に 2 次成分を追加します。2 次曲線の式は以下のようになります。
この式は、2 次曲線(放物線)を表す一般的な式です。回転成分はステップ 1、2 で除去されています。
この 2 次曲線は、以下に示す 3 つの点を通ります。

これらを使用することにより、温度係数 a、b、c を求めることができます。

すべての温度係数(ΔN0、ΔN1、ΔN2、a、b、c)の情報は、システムの不揮発性メモリに格納しておきます。また、システムには温度センサーが必要になります。そして、システムは、電源を投入した際に必ず加速度センサーのキャリブレーションを実行するように構成します。それにより、温度によるオフセットの変化を確実に補正します。
ノイズ
1 つのサンプリング・データを基にして行った傾斜測定は、信頼できない可能性があります。仮に、加速度センサーでは全くノイズが発生していなかったとします。そうだとしても、傾斜測定は自動車のエンジンがかかった状態で行われます。傾斜測定は、エンジン、通過車両、車内で体を動かす搭乗者などによってもたらされるすべての振動を抑えて行うべきです。そのための最良の方法は、最小データ・レートの要件を下回ることなく、できるだけ長い間にわたってデータを取得し、平均化を実施することです。この手法により、RMS ノイズを低減することができます。
ノイズのサンプリングを行い、以下のような分散が得られたとします。

確率変数に対する平均化により、以下の分散が得られます。

ノイズの分散は σ2 で一定なので、次の式が得られます。
同じ n 個の無相関ノイズの値を平均化すると、ノイズのパワーが 1/n に低減されます。そのため、RMS ノイズは1/√n に低減されることになります。
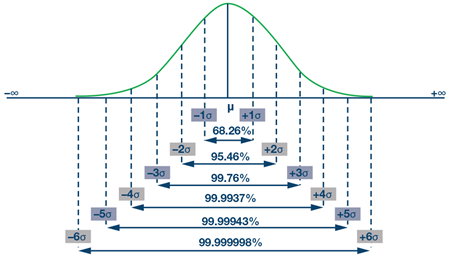
ランダム・ノイズはガウス分布に従います。したがって、RMS ノイズはガウス分布の標準偏差に等しくなります。6σ の範囲内に収まる確率は 97% 以上です。
例えば、1 kSPS のデータを 100 ミリ秒ごとに平均化するとします。その場合、RMS ノイズは最大で 0.4 mg となります。6σ を平均値からの距離として使用すると、その時点におけるピーク・ノイズの計算値はわずか 2.4 mg になります。
RMS 値に乗じる数値は、製品のミッション・プロファイルの統計的要件によって異なります。例えば、乗じる数値として 6 を選択する(ピーク to ピーク・ノイズをRMS ノイズの 6 倍とする)場合、その製品の使用期間中に最も厳しい条件が発生する確率が変化します。ここで、RMS ノイズは、製品のデータシートに記載された固定値です。RMS 値は標準偏差であり、1σ の範囲を意味します。1σ の範囲には 68.26% しか含まれないので、これを計算に使用するのは適切ではありません。そのため、RMS ノイズに乗じる数値としては、より大きい値を選択しなければなりません。乗じる数値が大きいほど、網羅する範囲が広くなります。
理論的には、RMS ノイズに乗じる数値によって、アルゴリズムを適用している期間中の故障回数が決まります。ノイズは、時間に対してランダムな変数であるからです。ノイズは予測可能なものではありませんが、統計的な計算によって答えを得ることは可能です。
EPB モジュールのアルゴリズムによる予測の実行回数が14 万 6000 回(1 日当たり 20 回で 20 年間)であるとします。使用期間中に一度の故障も許されないとすると、最大故障率は 1/146000 × 100 = 0.00068% となります。
ガウス分布における σ の範囲を見ると(図11)、6σ の範囲における不良率は 0.00034% です。そこで、RMS 値に乗じる数値として 6 を選択すると、146000 × 0.00034%= 0.5 < 1 となります。これは、統計的には、20 年の使用期間にわたって EPB モジュールが故障することはないということを意味します。
以上の内容をまとめると、次のような式として表すことができます。

ここで、E は使用期間においてワースト・ケースを上回ることが予想される回数です。M は使用期間におけるアルゴリズムの実行回数、r はワースト・ケースを上回る確率です。これに基づいて、RMS ノイズに乗じる数値を合理的に求めることができます。
まとめ
本稿は、アナログ・デバイセズの「ADXC1500」、「ADXC1501」をベースとして執筆しました。それぞれ、2 軸/3 軸の加速度センサーとジャイロスコープを組み合わせたコンボ品です。表 1 に、誤差に関連するすべての項目が、キャリブレーションの実施前後でどのような値になるのかをまとめました。オフセットの総変化量は 2 次曲線で表される性質を持ち、温度による変化量はオフセットの総変化量の 80% を占めると想定できます。また、RMS ノイズの最大値に乗じる数値は 6 としました。
ジャイロスコープと 3 軸加速度センサーを組み合わせることにより、新たなアプリケーションを実現することができます。特に、車載安全システムや産業用オートメーションの分野では、数多くの応用例を想定できます。堅牢な横滑り防止機能や横転検出機能などを実現する車載安全システムには、高い信頼性と精度が求められます。そのようなシステムを設計するには、本稿で示した誤差要因を最小限に抑えることが不可欠です。安全を確保するための各種技術は、ABS(アンチロック・ブレーキ・システム)、トラクション・コントロール機能、ヨー・コントロール機能など、自動車に搭載されている従来のシャーシ制御システムをベースとしています。
| 誤差要因 | キャリブレーションの実施前 | キャリブレーションの実施後 | キャリブレーション方法 |
| 感度誤差 | 30 mg | 0 mg | 2 点キャリブレーション |
| 初期絶対オフセット | 15 mg | 0 mg | 2 点キャリブレーション |
| 非線形性 | ±500 mg の範囲で 10 mg | ±500 mg の範囲で 10 mg | なし |
| オフセットの総変化量 | 50 mg | 10 mg | 3 点キャリブレーション |
| ノイズ | 24 mg | 2.4 mg | 100 回の平均化 |
| トータルの誤差 | 129 mg | 22.4 mg | |
| 精度 | 7.4°(ワースト・ケース) | 1.28°(ワースト・ケース) | 度 |
謝辞
本稿の執筆にあたり、多くの有益な意見を提供してくれたアナログ・デバイセズの Matthew Hazel と Brian Lariveeに感謝します。

