Phase Noise of Integer-N and Fractional-N PLL Synthesizers

Low phase noise is essential when generating high frequency, high linearity signal sources. Phase noise is a measure of the undesirable change or variation in phase of a signal. It is measured in the frequency domain and equates to jitter in the time domain. When using a PLL synthesizer, the total phase noise is made up of a compilation of the various circuit blocks and components that each contribute to the final value. The various contributing components/circuits include the voltage-controlled oscillator (VCO), the reference clock and associated circuitry, the phase-frequency detector and various internal buffers.

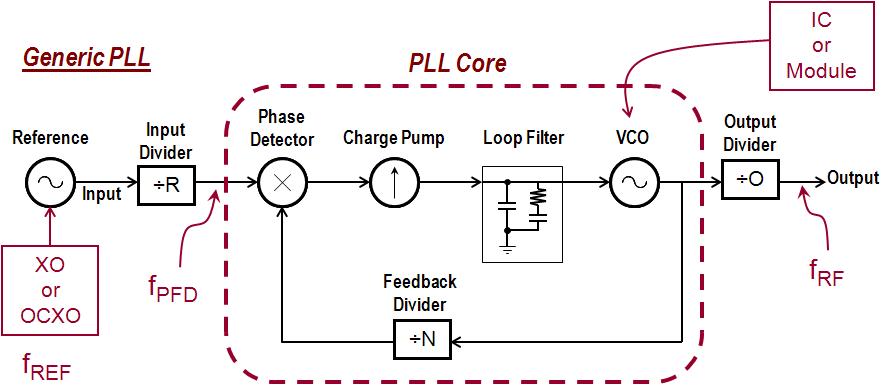
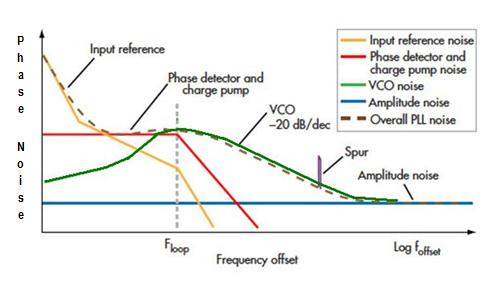
The phase noise can be separated into the contributing portions of each component/circuit and includes the reference noise, the phase frequency detector noise, the VCO noise, and wideband noise (due to amplifiers/buffers and other internal circuitry) that establishes the out-of-band phase noise floor.

 

 

When deciding between an integer-N vs. fractional-N PLL synthesizer, one must consider the significance of the total phase noise, cost, step-size, PLL design complexity, spurious noise (fractional spurs due to accumulator or delta sigma in a fractional-N), integer boundary spurs (also a fractional-N effect) and reference spurs) and the loop lock time. 

Advantages of a Fractional-N PLL

A fractional-N (frac-N) PLL synthesizer has several key advantages over an integer-N PLL, though in some instances these advantages may not be significant for the customer depending on the application. It allows larger reference frequency values, which results in a smaller multiplier term N. Since the PLL's phase noise is multiplied by the value of N chosen (f_OUT = f_REF * N) and frac-N PLLs require smaller values for N, the phase noise increase due to multiplying the reference frequency by N will decrease by 20log(N) dB, but this is partially offset by an increase in phase frequency detector noise of  - 10log(f_PFD) dB (for simplicity, we assume the reference divider value R is 1 so that f_REF = f_PFD; larger integer values result in even more noise). Another advantage is the smaller step-size or higher resolution. A frac-N allows step sizes on the order of tens of Hertz, while an integer-N may result in tens of kilohertz. The frac-N also will lock faster when compared to a similar integer-N solution. This is because the lower value of N allows a wider loop filter bandwith, which in turn allows a faster lock time.

Disadvantages of a Frac-N PLL

The biggest disadvantages of a frac-N PLL are the fractional and integer boundary spurs it generates, its increased complexity from a usage standpoint (the loop filter has to be designed) and in some instances a higher cost. These are reasons why a customer may opt for an integer-N PLL. LTC's new frac-N PLL devices mitigate these disadvantages. They are designed to yield very low integer boundary spurs, and their fractional divider uses an advanced, 4th order ΔΣ modulator, which produces no fractionalization spurs. With regard to complexity, our FracNWizard software features advanced PLL design and simulation capabilities, which simplify the loop design effort.

Examining the Data Sheet for Differences

When reviewing integer-N and frac-N data sheets, one may be confused by the fact that some of the phase noise specifications look similar, even though the frac-N supposedly has lower phase noise. For example, looking at the front page of the LTC6947 data sheet, three phase noise specifications are given in the "Features" section: the normalized in-band phase noise floor, the normalized 1/f noise and the wideband out-of-band phase noise floor. The values for each are -226dBc/Hz, -274dBc/Hz and -157dBc/Hz. For the LTC6945 the numbers are -226dBc/Hz, -274dBc/Hz and -157dBc/Hz.

 

 

 

The key is that the first two specifications are normalized. This means that they are calculated without consideration for the other circuit elements that are needed to complete the design, which allows engineers to do a side-by-side comparison.  However, this does NOT give the true value that will be obtained by the user; instead it is a "figure of merit". When we "unnormalize" the value in a real-world application, the PLL N divider value and the reference clock frequency are factors in the final value.

Normalizing is why a Frac-N and a Integer-N can have similar values.  When used in a typical application, a Frac-N will usually result in a much lower in-band phase noise because it generally allows for a much higher reference frequency (or PFD frequency), and as previously mentioned this yields a smaller value for the N-divider (N), which reduces the overall phase noise.

As an example, for an LTC6945 integer-N PLL synthesizer solution with a 100kHz frequency step size and a 3GHz output, the PFD is set to 100kHz. In the same example using the LTC6947 frac-N PLL, the PFD can be set at a much higher frequency. Let's chose 50MHz. This results in a maximum frequency error of ~100Hz (50MHz/2^18)/2 – the divide by 2^18 is because of the 18-bit delta sigma modulator used by the LTC6947), or 1000 times smaller steps.

Continuing the example, the in-band phase noise of the frac-N 3GHz output will be roughly 27dB lower than that of the integer-N assuming similar normalized in-band phase noise values (see pg. 21 of the LTC6947 data sheet Figure 11 for the complete equation). Though the LTC6947 frac-N PLL has 1dB worse normalized in-band phase noise in frac-N mode, it provides 26dB lower in-band phase noise floor than the LTC6945 integer-N.

One final note is that since the phase noise floor is not dependent on spurious components, both the frac-N and integer-N PLLs have a similar value.

Analog Devices offers both integer-N (LTC6945/LTC6946) and Frac-N (LTC6947/LTC6948) PLL synthesizers. Both types offer excellent phase noise performance. If smaller frequency step size and lowest phase noise is desired, a Frac-N is best. If lower cost and less complexity is desired, choose an integer-N PLL. Click here for our complete line of PLL synthesizers.