要約
This application note uses common data conversion theorems to analyze the impacts of resolution and sample rate in a band-limited signal generation application. The conclusion is that the SNR performance improvement, due to the 16-bit LVDS interface bus, provides improved signal-to-noise (SNR) over a 14-bit Interface bus.
Introduction
Analog Devices manufactures a family of 16-bit radio frequency digital-to-analog converters (RF DACs) designed to provide high performance, wide-band signal generation. The first device in this family was the MAX5868, which was introduced in 2012, employs a parallel 16-bit double-data rate (DDR) low-voltage differential signal (LVDS) interface bus. Figure 1 shows the simplified block diagram from the MAX5868 datasheet.

Figure 1. MAX5868 Simplified Block Diagram
One aspect of the design has resulted in an oft-repeated question: Why is the interface 16 bits yet the DAC is shown as 14 bits in the MAX5868? A short and sweet explanation is that the noise floor is determined by quantization noise, thermal noise, and jitter noise (clock noise). If the input interface were only 14 bits, the quantization noise would dominate the thermal noise.
The resolution of a data converter has a direct impact on the SNR performance of the device. In the case of a DAC, there are three primary sources of output noise: thermal noise, jitter noise, and quantization noise. These sources combine to determine the total SNR as shown in the following calculation:
 Equation 1
Equation 1
Where:
SNRQUANT = SNR due to quantization
SNRJIT = SNR due to clock jitter
SNRTHERM = SNR due to thermal noise
Another common theorem in data conversion is the calculation of ideal SNR as a function of device resolution assuming no thermal or jitter contributions; in other words, the SNR due to only quantization (SNRQ) as follows:
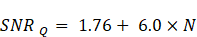 Equation 2
Equation 2
Where:
N = number of bits of resolution.
While Equation 2 is most often mentioned in reference to analog-to-digital converters (ADCs), it is equally useful in determining the impact of quantization noise in DAC applications. The result of the calculation applied to DACs is the aggregate noise within the entire Nyquist bandwidth due to quantization.
The SNR due to quantization is useful information, but we need to compare this against the other terms in Equation 1 to determine the impact of the resolution of the DAC and input interface. We also need to consider the update rates at the various stages to make the comparison meaningful. In order to facilitate this analysis, we will convert the calculated SNRQ to an ideal noise spectral density (NSDQ) due to quantization. We will also estimate the level for the SNRTHERM (NSDT) term against which the quantization noise will be compared.
The results will show that the NSDQ level at each stage of the MAX5868 ensures that the thermal noise is dominant and that further increases to the core DAC resolution are unwarranted.
Calculating Noise Spectral Density Due to Quantization
Noise spectral density is a measure of the noise power, typically expressed in dBm or dBmV, within a specified bandwidth and usually normalized to 1Hz. Since this is an absolute power, we will use the full-scale output power specification of the DAC as our reference point, allowing the conversion of SNRQ to noise density due to quantization.
The first step in the conversion to NSD is to calculate the total noise power due to quantization within the Nyquist BW. We will call this term PQ and compute it as follows:
 >Equation 3
>Equation 3
where:
PF = the output power specification of the DAC, in dBm and based on a full-scale sinewave.
The next step is the conversion of the noise power to a power spectral density value. We will assume that the noise is evenly distributed across the Nyquist zone of the converter and use it in the following equation:
 Equation 4
Equation 4
where:
BW = Nyquist Frequency
Now, let us apply the above theory using the MAX5868 specifications. First, we will look at the core 14-bit DAC independent of the input interface. Then, we will examine the input interface and see how the resolution and sample rate affect performance.
The full-scale output power specification of the MAX5868 is 0dBm when generating a 100MHz sinewave using a 4.96Gsps update rate. The parameters then for the three equations needed to compute NSDQ14 (Equations 2, 3, and 4) are as follows:
N = 14, DAC core resolution, (Eq. 2)
PF = 0, DAC full-scale output power (PF) (Eq. 3)
BW = 2.48GHz, fDAC/2 (Eq. 4)
Substituting these values give the following results.



Now let us look at the NSDQ16, noise density at the input interface using 16 bits. We first note that Analog's 16-bit RF DAC products all use interpolation between the input interface and the DAC core. The use of interpolation reduces the frequency of the input data, which in turn reduces the Nyquist BW. The interpolation rates for the Analog RF DAC portfolio of products can range from 4 times to as much as 24 times the DAC input data rate (fDATA). The upper limit for the input data rate is 625MHz, DDR, for the MAX5868 device. The DDR data is sent to the DAC as complex values: 16 bits of I and 16 bits of Q, interleaved in time. These combine through complex modulators to provide a Nyquist BW of 625MHz (625MHz I + 625MHz Q = 625MHz BW). Substituting these values (16 bits, and 625MHz BW) in Equations 2 and 4 results in a NSDQ16 of -182.5dBm.



We have now calculated two values for SNRQ that will be used to calculate two SNRTOTAL values, one for the input resolution (16 bits) and one for the output (14 bits). Next, we will determine the thermal noise contribution at the DAC output. The common definition for calculating thermal noise is given in the following equation:
 Equation 5
Equation 5
Where:
k = Bolzmann's constant, 1.38064852 × 10-23m2kg s-2 K-1
B = Bandwidth in Hertz
T = Temperature in Kelvin
The resultant NSDT is -173.9 dBm/Hz when calculated for a 1Hz BW at 25°C (298.15°K).
By simply comparing these three NSD results (NSDQ14, NSDQ16 and NSDT), we see that the noise contribution due to quantization is below the thermal noise floor; ~2.5dBm/Hz lower at the DAC output, and nearly 12dBm/Hz lower at the digital input. However, to complete the exercise, we will calculate SNRTOTAL.
The total SNR equation from above has three terms, all in SNR, that are required for a solution. We have calculated only one of these, we must convert the thermal noise spectral density (NSDT) value to SNRT, and we need SNRJ which we have yet to address. In fact, SNR due to clock jitter is a subject for another time and for the sake of this exercise, we will assume NSDJ and NSDT to be equal and substitute that value for these two terms. The calculation of SNR due to thermal noise is a two-step process. The first step is to integrate the NSD over the Nyquist bandwidth to get the total noise power. Once we have the noise power, we can calculate it in relation to a full-scale DAC signal, or 0dBm as specified for the MAX5868. The resulting SNRT value is 75.84 for the 14-bit DAC core. The actual calculations are shown below.
 (thermal noise power over Nyquist)
(thermal noise power over Nyquist)


 SNR due to thermal noise
SNR due to thermal noise
Substituting the values back into the SNRTOTAL equation, we arrive at:


 Total theoretical SNR for 14-bit resolution
Total theoretical SNR for 14-bit resolution
Finally, let us recalculate the total SNR using a 16-bit DAC input interface at 625MHz:


 >Total theoretical SNR for 16-bit resolution
>Total theoretical SNR for 16-bit resolution
Comparing Results
The discussion and calculation of quantization noise and SNR may be interesting, it does not really explain why the MAX5868 has a 16-bit interface and a 14-bit DAC. Tables 1 and 2 show the noise (NSD and SNR) for 12-bit to 16-bit resolutions and sample rates of 625MHz and 4.915MHz. The interesting fact is that the resolution has no impact on the total SNR at a given sample rate.
| Resolution (Bits) | Update Rate (MHz) | SNRQ (dB) |
NSDQ (dBm/Hz) |
SNRTOTAL (dB) |
| 12 | 6.25E+08 | 74 | -1.59E+02 | -91.96 |
| 13 | 6.25E+08 | 80.02 | -1.65E+02 | -91.96 |
| 14 | 6.25E+08 | 86.04 | -1.71E+02 | -91.96 |
| 15 | 6.25E+08 | 92.06 | -1.77E+02 | -91.96 |
| 16 | 6.25E+08 | 98.08 | -1.83E+02 | -91.96 |
| Resolution (Bits) | Update Rate (MHz) | SNRQ (dB) |
NSDQ (dBm/Hz) |
SNRTOTAL (dB) |
| 12 | 4.92E+09 | 74 | -1.68E+02 | -83.01 |
| 13 | 4.92E+09 | 80.02 | -1.74E+02 | -83.01 |
| 14 | 4.92E+09 | 86.04 | -1.80E+02 | -83.01 |
| 15 | 4.92E+09 | 92.06 | -1.86E+02 | -83.01 |
| 16 | 4.92E+09 | 98.08 | -1.92E+02 | -83.01 |
However, these tables also show that noise spectral density due to quantization noise (NSDQ) is directly impacted by resolution and the update rate, while the SNRTOTAL is only impacted by the update rate. Comparing a given resolution across sample rates, it is clear that the total SNR is dominated by the thermal and clock jitter noise terms, and while the SNRQ improves by 6dB for every additional bit, the total SNR is flat regardless of the resolution.
Conclusion
Optimizing the performance of a DAC involves many considerations. To ensure the device has adequate resolution for a given task, the quantization noise must be considered at each stage in the digital domain, especially when interpolation is employed. While the 12- to 16-bit resolution has no impact on the total theoretical SNR, the increase of the sample rate does distribute the quantization noise over a wider region, effectively lowering the noise floor (NSD).




















