要約
このアーティクルでは、信号の元の情報を消失することなくサンプリングと復元をおこなうための理論的な手法を示します。また、エイリアシングの効果についても取り上げます。オーバサンプリングとアンダサンプリングの入力周波数の比較例としてMAX19541 ADCを使用します。
この記事に類似した内容が、2005年1月号の「RF Design」誌に掲載されています。
はじめに
最近のアプリケーションでは、ほとんどの場合、アナログ信号をサンプリングしてディジタル形式に変換し、その信号に対していろいろな操作を行ってから、最終的にアナログ信号に復元することが必要となります。この記事で考察する主要な問題点は、元の情報を完全に保持した状態でどのようにしてアナログ信号をサンプリングして復元するかということです。
帯域制限された信号
はじめに、帯域制限された信号に限定して考察します。その理由は、後で述べるように、数学的また物理的に表すことができるからです。信号のスペクトル振幅が、カットオフ周波数と呼ばれるスレッショルドを超えたすべての周波数に対してゼロになる場合に、その信号は帯域制限されているといわれます。図1のG(f)がこのような信号ですが、αを超える周波数についてはスペクトルがゼロです。この場合、値αが、このベースバンド信号の帯域幅(BW)でもあります(ベースバンド信号αの帯域幅は正の周波数についてのみ定義されています。負の周波数は実世界では意味を持たないからです)。
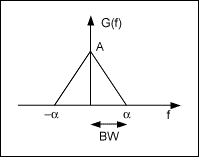
図1. 信号G(f)の周波数スペクトル
次のステップは、g(t)のサンプリングを実施することです。この動作は、間隔Tによって分離されたデルタ関数の列をg(t)に乗算することによって、数学的に表すことができます。デルタ関数をg(t)に乗算することによって、デルタ関数が生じた時点に一致するg(t)の値のみを選択します。つまり、他のすべての時刻についての積はゼロに等しくなります。これは、周波数fSAMPLING = 1/Tでg(t)をサンプリングすることと類似しています。この動作は、式1で表されています。サンプリングされた新しい信号が、s(t)です。

次のステップは、サンプリングされた信号s(t)のスペクトルを求めることです。これは、フーリエ変換を行うことで得られます。

上記の積分の計算は少し厄介です。これを簡略にするために、s(t)がg(t)とインパルス列の実効乗算値であることに注目します。また時間領域における乗算が、周波数領域の畳み込みに相当することにも注目してください(この主張の証明については、フーリエ変換についてのテキストを参照してください)。S(f)は、次式で表されます。

また、式3のアスタリスクが、乗算ではなく畳み込みを表していることに留意してください。元の信号g(t)のスペクトルは既知であるため、後はインパルス列のフーリエ変換を求めるだけです。これを実行するには、インパルス列が周期関数であること、したがってフーリエ級数で表せることを認識する必要があります。結果は、次式のようになります。

ここで、フーリエ係数は、次のようになります。

式5において、積分の範囲は1周期についてのみ規定されています。これは、デルタ関数を取り扱う場合に問題にはなりません。ただし、次の置換を行えば、上式をより確実なものにすることができます。すなわち、積分は、負の無限大から正の無限大までのフーリエ積分に置き換えることが可能で、デルタ関数の周期列は単一デルタ関数、すなわち周期信号のベースに置き換えることができます。この結果、次のように式5を書き換えることができます。
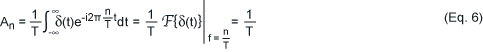
次に、デルタ関数の列は、以下の簡易な数式で表すことができます。この数式は容易にフーリエ変換が可能です。

信号はフーリエ変換から合成することができるため、次のようになります。

また、以下も成立します。
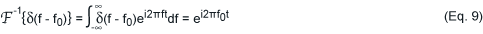
最終的に、次式で表すことができます。

この結果が得られた後、サンプリングしたベースバンド信号に再び注目しましょう。ここでは、フーリエ変換を次式で表すことができます。

2つの信号A(f)とB(f)の畳み込みは、次のように定義されます。

また、S(f)は、以下のように表すことができます。

式13は、ここまでの考察の結果ですが、これは一般的にサンプリング定理と呼ばれます。時間領域におけるT秒間隔でのサンプリングによって、非サンプリング信号のスペクトルを毎秒1/Tサイクルで繰り返すことを示しています。図2は、結果をグラフで表しています。この結果によって、最初の問題点に明確かつ直観的に答えることが可能になります。つまり、どのようにして、元の信号の情報を完全に保持した状態でサンプリングするかということです。

図2. サンプリングした信号s(t)の周波数スペクトル
エイリアシングの影響
サンプリングされていないベースバンド信号のすべての情報を保持するには、スペクトルを繰り返すときにスペクトルの「島」を重複させないようにすることが必要です。重複してしまった場合(この現象をエイリアシングという)、サンプルから元の信号を抽出することはできなくなります。図3に示すように、エイリアシングによって、見かけ上、高い周波数が低い周波数になってしまいます。

図3. エイリアシングの影響を受けた信号の図
エイリアシングを回避するには、1/T ≥ 2αすなわち1/T ≥ 2BWの条件を維持する必要があります。この結果は、サンプリング周波数に関して、次のように表すことができます。

このように、エイリアシングが生じないサンプリングに必要な最小限のサンプリング周波数は2BWです。この結果は一般的に、ナイキスト基準として知られています。
図3は、エイリアシングの影響を受けたサンプリング信号を表しています。高周波成分fHがはるかに低い周波数で現れることに留意してください。ローパスフィルタを使用して元のスペクトルを分離し、他のすべてのスペクトルを削除する(減衰させる)ことによって、サンプリング信号から信号を回復することができます。つまり、カットオフ周波数αのローパスフィルタで信号を抽出しても、エイリアシング高周波は除去されず、対象となる信号は破損されるということです。
エイリアシングによって対象の信号が破損されることを念頭において、バンドパス信号と呼ばれる特殊な帯域制限の信号を検討します。バンドパス信号は、下限がゼロでない帯域幅を特徴とします。図で説明すると、図4に示したバンドパス信号は、周波数αLとαUの間に信号エネルギを持ち、帯域幅はαU - αLと定義されます。したがって、バンドパス信号とベースバンド信号の主な違いは、帯域幅の定義にあります。つまりベースバンド信号の帯域幅は、その最大周波数に等しくなりますが、バンドパス信号の帯域幅は上限と下限の周波数の差になります。

図4. バンドパス信号の説明図
これまでの考察から、この信号のサンプリングによって1/Tの間隔でそのスペクトルを繰り返すということがわかります。このスペクトルには、ゼロと、その信号の下限周波数の間に大幅なゼロ振幅帯域が含まれているため、実際の信号帯域幅はαUより小さくなります。したがって、周波数領域においてより小さな偏移を使用することが可能で、スペクトルがゼロからαUまでのすべての周波数を占有する信号の場合に必要な周波数より低いサンプリング周波数が可能となります。たとえば、αU/2の信号帯域幅を想定します。ナイキスト基準を満たすには、サンプリング周波数はαUに等しくなり、サンプリング信号のスペクトルは、図5のようになります。

図5. サンプリングしたバンドパス信号のスペクトル
このサンプリングではエイリアシングは発生していません。したがって、完全なバンドパスフィルタがあれば、サンプルから元の信号を取り出すことができます。この例では、ベースバンド信号とバンドパス信号間の差異に留意することが重要です。ベースバンド信号の場合には、帯域幅したがってサンプリング周波数は単に、存在する最大周波数によって決まります。バンドパス信号の場合には、帯域幅は通常、最大周波数よりも小さくなります。
これらの特性によって、サンプリング信号の回復方法が決まります。最大周波数の値が同じであるベースバンド信号とバンドパス信号を考えてみます。バンドパス信号では、回復方法に元の信号スペクトルを分離するバンドパスフィルタが含まれる場合にのみ、より低いサンプリング周波数が許されます(図5の白い四角形の部分)。ベースバンドの回復に使用されるローパスフィルタは、元のバンドパス信号を回復することはできません。図5に示す網掛け領域が含まれるからです。したがって、ローパスフィルタを使用して図5のバンドパス信号を回復する場合、エイリアシングを回避するために2αUでサンプリングする必要があります。
このように、帯域制限された信号は、ナイキスト基準が守られている場合にのみサンプリングして完全に回復することが可能です。バンドパス信号の場合、信号の回復がバンドパスフィルタで行われているときにのみ、ナイキスト基準によってエイリアシングが発生しないことが保証されます。それ以外の場合は、さらに高いサンプリング周波数が必要です。この認識はどのアナログ-デジタルコンバータのサンプリング周波数を選択する場合でも重要です。
最後に考慮すべき点は、帯域制限された信号に関する前提です。数学的には、信号は決して本当の意味で帯域制限することはできません。フーリエ変換の定理では、信号が時間的に有限である場合、スペクトルは無限の周波数にまで拡大され、またその帯域幅が有限であれば、その期間は時間的に無限となります。当然ですが、期間が無限の時間領域信号は不可能であるため、本当の意味で帯域制限された信号は得られないということになります。ただし、実際の信号のほとんどは、スペクトルの限られた部分に多くのエネルギが集中しています。上述の分析はこのような信号には有効です。
正弦波信号のサンプリング
エイリアシングに固有の、高い周波数が低い周波数に見えてしまうという現象を説明する極めて簡単で都合のよい実際的な方法は、正弦波信号をサンプリングすることです。純粋な正弦波信号のスペクトルは、各周波数におけるスパイク(デルタ関数)のみで構成されているからです。したがって、純粋なトーンによるエイリアシングは、スパイクがある場所から別の場所へ移動するときに見られます。この、別の場所はイメージと呼ばれますが、実際にはエイリアシング信号です。
以下に示した結果は、MAX19541の125Msps、12ビットADCで取得したものです。図6は、入力周波数fIN = 11.5284MHzの場合のコンバータ出力におけるスペクトルを示しています。このデータは、主要なスパイクがちょうどこの周波数で発生することを示しています。他にも、コンバータの非直線性によって生じる高調波のスパイクがいくつかありますが、ここでの議論とは関係ありません。サンプリング周波数fSAMPLING = 125MHzは、ナイキスト基準で求められる、入力周波数の2倍以上であり、したがってエイリアシングは発生しません。

図6. MAX19541 ADCでサンプリングした信号のスペクトル。ここでは、fSAMPLING = 125MHz、fIN = 11.5284MHzです。
次に、入力周波数をfIN = 183.4856MHzに増大したときに主要なスパイクの位置がどうなるかを考えてみます。この入力周波数はfSAMPLING/2より大きいため、エイリアシングの発生が予想されます。得られたスペクトルを図7に示します。主要なスパイクの位置が58.48MHzに変化していること、またこれがエイリアシング信号であることがわかります。言い換えると、58.48MHzにイメージが現れますが、実際にはこの周波数は入力信号に含まれていません。図6と図7のどちらについても、ナイキスト周波数までのスペクトルだけをプロットしていることに留意してください。これは、スペクトルは周期的なものであり、この部分に基本的な情報がすべて含まれているからです。

図7. MAX19541 ADCでサンプリングした信号のスペクトル。ここでは、fSAMPLING = 125MHz、fIN = 183.4856MHz




















