電流モードステップダウンコントローラ用の正確な制御ループモデル

要約

ピーク電流モード制御が電源設計者に好まれるのは制御入力と出力間の伝達関数が一次周波数応答特性となるためです。一次モデルを基にした制御ループの設計手法は90°に近い位相マージンが期待されます。しかし、実際に得られる位相マージンはクロスオーバ周波数、動作デューティサイクル、およびスロープ補償の大きさに依存して90°よりもずっと小さくなります。これは制御ループの電流コンパレータのサンプリングの影響によります。以下に述べるアプリケーションノートはこのサンプリングの影響を考慮して、正確に位相マージンを予測するMAX1954A電流制御コントローラに対する制御ループの設計手法を説明しています。しかし、ここで述べる解析はMAX1954Aに固有ではなく、現在売られているほとんどの電流モードステップダウンICに適用可能です。

一次モデル

図1にステップダウンコンバータの標準的な電流モード制御ループが示されています。一定周波数のクロックCLKがハイサイドMOSFETをオンにします。PWMコンパレータの反転入力におけるスケール変換したインダクタ電流が制御電圧のv_cを超えるとQ1はオフになります。このように、vcによってピークのインダクタ電流が設定されて出力電圧のv_oが一定になります。このことによって出力インダクタの電流源の振舞いが決定されて、制御入力から出力までの伝達関数が一次特性になります。補償ランプのv_sがPWMコンパレータの二番目の反転入力に与えられて、0.5を超えるデューティサイクルでのサブハーモニックスによる不安定性を防ぎ、ノイズ耐性を改善します。電流モード制御に関連する波形が図2に示されています。

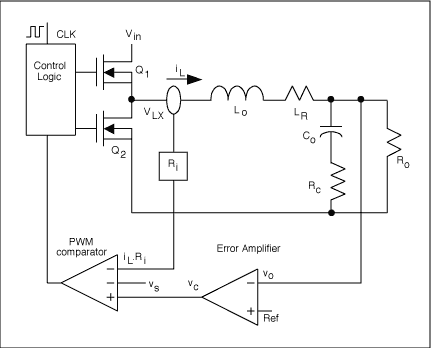
Figure 1. Peak current-mode control scheme.

図1. ピーク電流モード制御方式

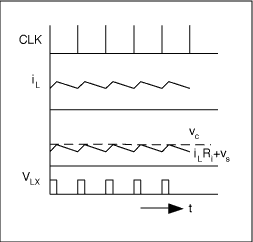
Figure 2. Current-mode control waveforms.

図2. 電流モード制御波形

ピーク電流モードコントローラの設計で使われる制御入力と出力間の伝達関数は次の式で与えられます。

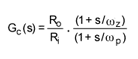
Equation 1

上の式は出力コンデンサC_oと負荷抵抗R_oによるポールのω_pを決定します。この式は出力コンデンサとその等価直列抵抗(ESR)のR_cによるゼロのω_zも決定します。上のモデルで決定される利得と位相は実際に観測される値とは異なりますが、その理由は各サイクルで1回だけサンプルされる電流波形によるPWMコンパレータ内の｢サンプルホールド｣効果によるためです。サンプリング効果を考慮するには上述の式による簡単なピーク電流モード制御モデルはスイッチング周波数の半分の周波数にあるダブルポールを含むように変更しなければならないことが[1]に示されています。

位相マージンを求める方法

次に電流モードコントローラのMAX1954Aに対してこの高周波効果を考慮し、位相マージンを正確に求める制御ループの設計手法を説明します。この設計を行うためにMAX1954Aの評価キットの回路図を使用します。MAX1954Aの評価キットのデータシートとMAX1954Aのデータシートの両方が入手可能です。

正確な制御入力と出力間に伝達関数は次の式で与えられます。

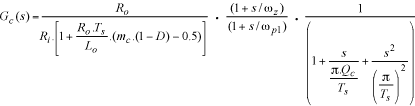
Equation 2

ここでデューティサイクルは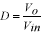、サンプリング効果特性係数は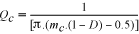、スロープ補償係数は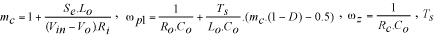はスイッチング周期、S_eはスロープ補償ランプ(補償している場合)、R_iは電流検出アンプの利得と電流検出抵抗(MAX1954Aの場合はハイサイドMOSFETのR_{ds_on})の積、R_oは負荷抵抗、V_oは出力電圧、そしてV_inは入力電圧です。MAX1954Aの評価キットの回路では以下の設計パラメータが適用されています。

V_in = 11V
V_o = 1.5V
D = 0.136
m_c = 1
S_e = 0 (MAX1954Aの場合、このデューティサイクルで印加されるスロープ補償はごくわずかです)
T_s = 3.3µS
R_c = 9mΩ
C_o = 180µF
L_o = 2.18µH
R_o = 0.3125Ω
R_i = 0.063

補償回路はMAX1954Aのデータシートの推奨どおりに設計します。正確なモデルで予測される制御入力と出力間の伝達関数およびオープンループ利得はMathCadを用いてプロットして、図3と図4に示します。MAX1954Aの評価キットで測定した実際の制御入力の出力間のループ利得およびオープンループ利得の伝達関数は、それぞれ、図5と図6に示します。

Figure 3.Control-to-output gain and phase plots from MathCad.

図3. MathCadによる制御入力と出力間の利得と位相のプロット

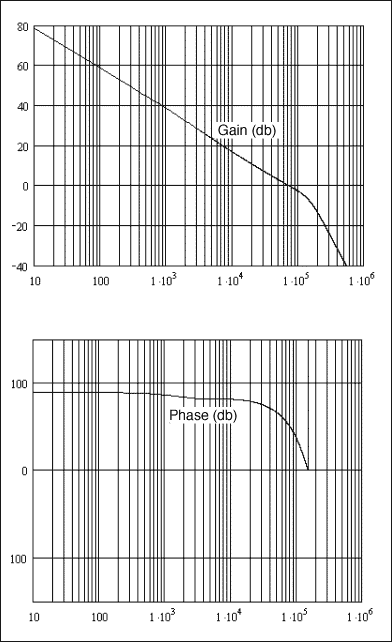
Figure 4.Open-loop gain and phase plots from MathCad.

図4. MathCadによるオープンループの利得と位相のプロット

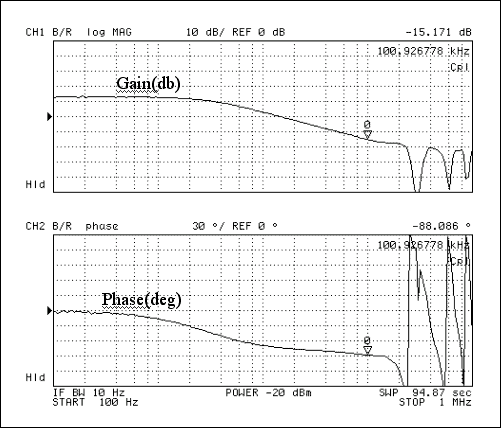
Figure 5. Measured control-to-output gain and phase plots.

図5. 測定された制御入力と出力間の利得と位相のプロット

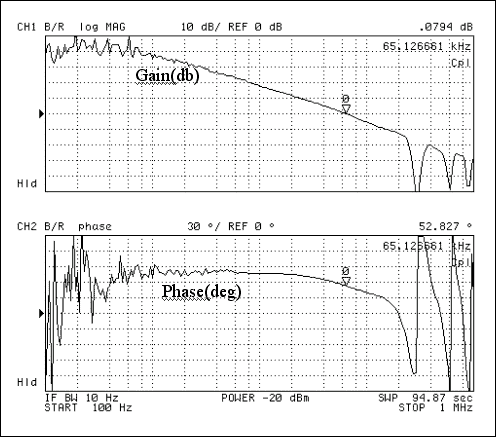
Figure 6.Measured open-loop gain and phase plots.

図6. 測定されたオープンループの利得と位相のプロット

モデルから予測した制御入力と出力間の利得と位相は測定した値によく一致しています。101kHzでは、モデルでは利得は-13.5dBで位相遅れは-95°です。この測定されたプロットでは-15.1dBの利得と-88°になります。モデルによるオープンループ利得および位相のプロットからクロスオーバ周波数が70kHzで位相マージンは56°を示しています。測定プロットではクロスオーバ周波数は65kHzで位相マージンは52.8°です。一次モデルはおよそ90°の位相マージンと予測され、構成部品のより大きなバラつきを許容します。したがって、正確な安定性のマージンを得るためには、クロスオーバ周波数が低いピーク電流モードの設計においても、サンプリングの効果を考慮するモデルの使用を推奨します。