AN-1094: Multiplying DACs—Fixed Reference, Waveform Generation Applications
Introduction
Used with an amplifier with sufficient ac performance, a multiplying digital-to-analog converter’s (DAC) R-2Rarchitecture makes it ideal for low noise, low glitch, fast settling applications. This application note details the basic theory behind current output multiplying DACs, and why these DACs are suitable for waveform generation from a fixed dc input reference.
Basic Theory
Multiplying DACs offer an ideal building block for waveform generation applications. The buffered current output DAC architecture is based on a noninverting gain amplifier structure. A multiplying DAC uses an R-2R architecture to replicate the functionality of the variable RDAC resistor shown in Figure 1. The input impedance to the DAC seen at the VREF pin is fixed, while the output impedance is code dependent to give the equivalent variable RDAC value. See also, www.analog.com/MultiplyingDAC.
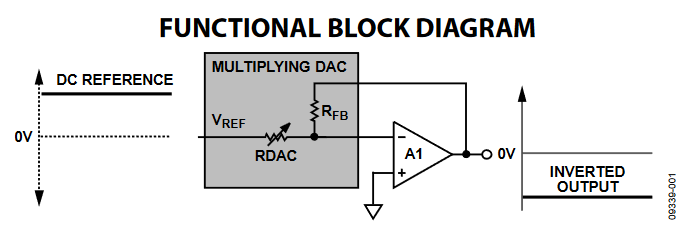
Figure 1. Unipolar Inverting Configuration.
The terms AD55xx and AD54xx used in this application note reference the multiplying DACs listed on www.analog.com/MultiplyingDAC.
Multiplying DACs
In a multiplying DAC, current is steered to either the virtual ground connected to the IOUT1 node or the ground node (in some parts this is the IOUT2 node), which allows for a very low glitch output voltage (see Figure 2).
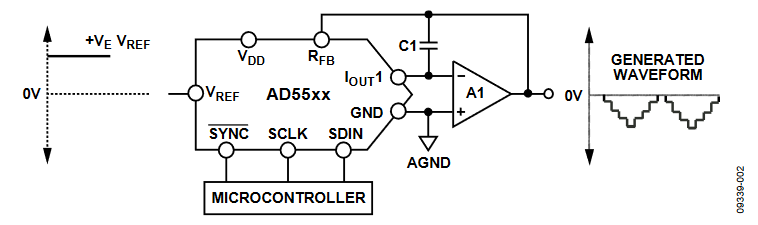
Figure 2. Multiplying DAC, VOUT = 0 V to −VREF.
One of the key advantages in using an IOUT DAC in this configuration is that the integrated RFB resistor is matched to the RDAC equivalent resistor allowing for very low gain temperature coefficient errors.
When an output amplifier is connected in unipolar mode, as shown in Figure 2, the output voltage is given by:
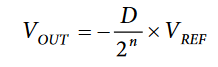
where:
D is the fractional representation of the digital word loaded to the DAC.
D = 0 to 255 (8-bit AD5450)
= 0 to 1023 (10-bit AD5451)
= 0 to 4095 (12-bit AD5452)
= 0 to 16,383 (14-bit AD5453)
= 0 to 65536 (16-bit AD5543)
n = the number of bits.
The output signal of a multiplying DAC is proportional to the product of the reference input and the digital input number.
Bipolar Operation
In some applications, it may be necessary to generate a bipolar output voltage from a fixed input reference voltage. This can be easily achieved by adding a second amplifier and some external resistors as shown in Figure 3.
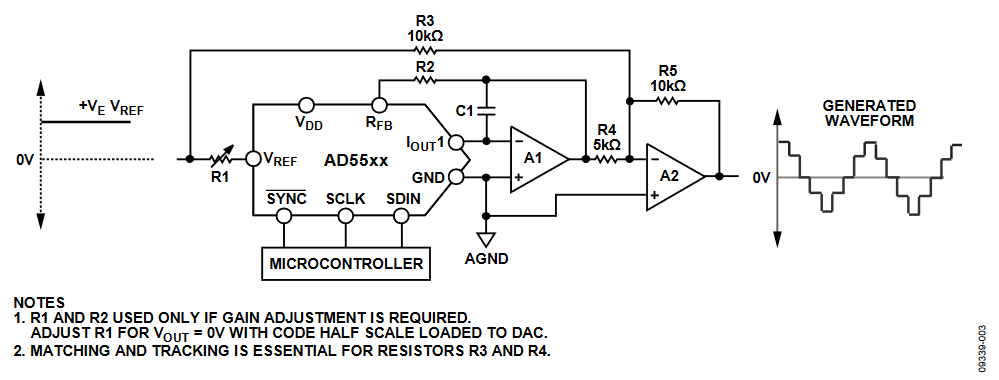
Figure 3. Multiplying DAC, VOUT = −VREF to +VREF.
The second amplifier basically provides a gain of 2, where biasing the external amplifier with an offset from the reference results in bipolar operation.
The transfer function of this circuit shows that both negative and positive output voltages are created as the input data (D) is incremented from zero scale (VOUT = −VREF) to midscale(VOUT = 0 V ) to full scale (VOUT = +VREF).
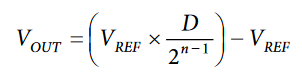
Positive Voltage Input/Positive Voltage Output
To generate a positive voltage output, an external inverting op amp circuit can be used to provide an additional inversion of either the input or the output. Because some multiplying DACs include uncommitted matched resistors (with tracking temperature coefficients), a positive output can be obtained simply by connecting an additional op amp (A2 in Figure 4), which could be the companion op amp within a dual device.
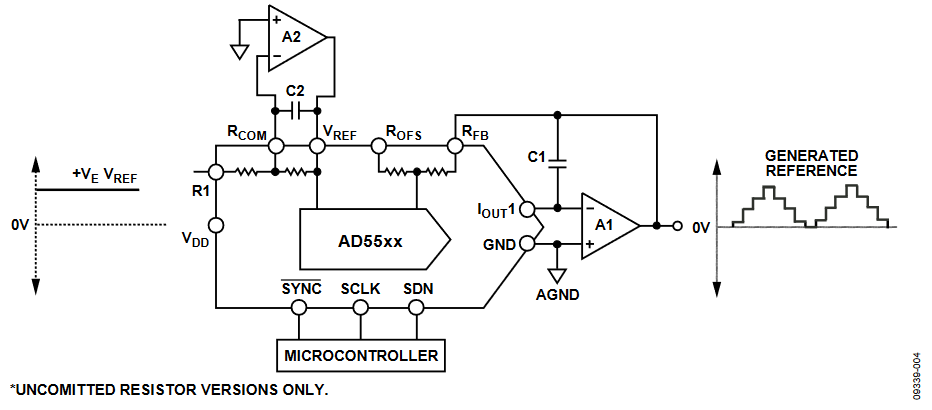
Figure 4. Multiplying DAC, VOUT = 0 V to VREF.
Stability Issues
An important component to take into account in achieving the desired waveform conditioning signal is the compensation capacitor. The internal output capacitance of the DAC introduces a pole into the open-loop response that can cause ringing or instability in the closed-loop ramp profiling circuit. To compensatefor this, an external feedback capacitor, C1, is usually connected in parallel with the internal RFB of the DAC (see Figure 2). If the value of C1 is too small, it can produce ringing at the output, and if the value of C1 is too large, it can adversely affect the settling time of the system. Because the internal output capacitance of the DAC varies with code, it is difficult to fix a precise value for C1. The value is best approximated according to the following equation:
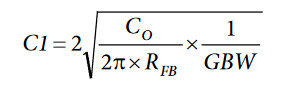
where:
GBW is the small signal unity gain bandwidth product of the op amp in use.
CO is the output capacitance of the DAC.
Key DAC Specifications for Waveform Generation
Some of the key selected ac specifications that must be taken into account when generating a waveform from a fixed reference input voltage include settling time, midscale glitch, and digital SFDR.
Settling Time
Provided the DAC is driven from true wideband low impedance sources (reference voltage and grounding pins), it settles quickly. Consequently, the slew rate and settling time of a multiplying DAC is predominantly determined by the op amp. Among the specifications that determine the ac performance of the op amp are its input capacitance, which must be kept to a minimum and the 3 dB small signal bandwidth. Note that the bandwidth of an op amp is limited due to the large load it has to drive in the feedback resistor of the DAC. A feedback resistor of, for example, 10 kΩ is a significant load to drive and is the dominating pole in determining the bandwidth of the circuit configuration.
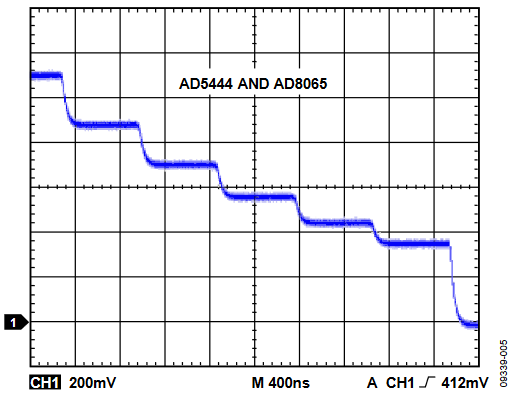
Figure 5. 100 ns Settling Time.
Midscale Glitch
For an R-2R structure, the major glitch, caused by a code change, occurs at the 1 LSB change around midscale. In a 12-bit system, such as the AD5444, the midscale change is the 7FFH to 800H code change or the 800H to 7FFH code change. If significant, these glitches can have an unwanted affect in any motor/valve/actuator control application. When the multiplying DAC tries to change from 7FFH to 800H, the MSB switch in the DAC switches at a slower speed then the other switches. Therefore, for a few nanoseconds, the DAC sees 000H before the MSB switch is set to 1. The orange trace in Figure 6 is an example of this, where the output heads towards 0 V before the MSB switches and brings the DAC output back to 800H.
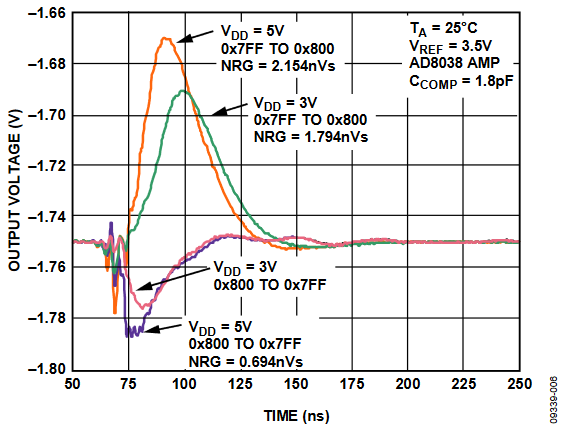
Figure 6. Midscale Glitch.
Digital SFDR
Spurious-free dynamic range (SFDR) is the usable dynamic range of a DAC before spurious noise interferes or distorts the fundamental signal. SFDR is the measure of difference in amplitude between the fundamental and the largest harmonically or nonharmonically related spur from dc to full Nyquist bandwidth (half the DAC sampling rate). Narrow-band SFDR is a measure of SFDR over an arbitrary window size.
An ideal sine wave has an infinite number of points per cycle. However, a digitally created sine wave is limited by the fixed update rate and resolution of a DAC. The number of points per cycle is given by:
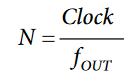
where:
N = number of sample points.
Clock = update rate of DAC.
fOUT = output frequency of a generated waveform.
For Figure 7, a 12-bit AD5444 is used to generate a 20 kHz sine wave with an update rate of 1 MHz. This gives 50 sample points per period. The AD5444 has a maximum update rate of 2.7 MSPS. To generate a waveform with more sample points a faster update rate is required. A parallel interfaced AD5445 has an update rate of 20 MSPS.
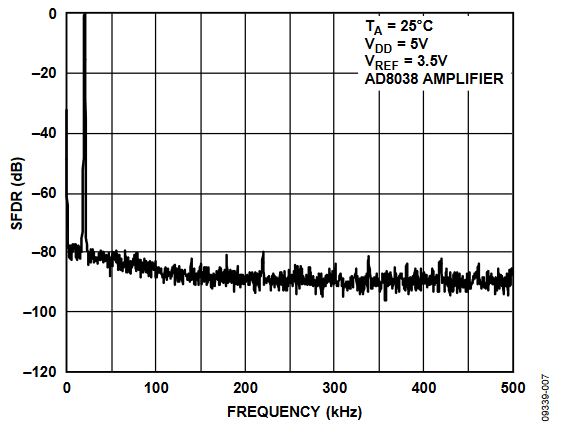
Figure 7. Wideband SFDR, fOUT = 20 kHz, Clock = 1 MHz.
Choosing The Correct Op Amp
Multiplying DAC circuit performance is strongly dependent on the ability of the selected op amp to maintain the voltage null at the ladder output and perform the current-to-voltage conversion. For best dc accuracy, it is important to select an operational amplifier with low offset voltage and bias current to keep errors commensurate with the resolution of the DAC. Detailed op amp specifications are included in device data sheets.
For applications where a digital waveform is to be generated from a fixed dc reference, a high slew rate, high bandwidth, low noiseop amp isrequired. This is to ensure that the output voltage settles accurately and quickly enough before the next DAC code change.
The gain bandwidth of an op amp circuit is limited by the impedance level of the feedback network and the gain configuration. To determine what GBW is required, a useful guideline is to select an op amp with a –3 dB bandwidth that is 10 times the frequency of the reference signal.
If the slew rate of the op amp is not given careful consideration, it can limit the multiplying DAC. As a rule for the AD54xx and AD55xx parts, an op amp with a slew rate of 100 V/µs is generally sufficient.
Table 1 is a selection of operational amplifiers that can be used for multiplying applications.
| Part No. | Supply Voltage (V) | BW @ ACL (MHz) | Slew Rate (V/µs) | VOS (Maximum) (µV) | IB (Maximum) (nA) | Packages |
| AD8065 | 5 to 24 | 145 | 180 | 1500 | 0.006 | SOIC-8, SOT-23-5 |
| AD8066 | 5 to 24 | 145 | 180 | 1500 | 0.006 | SOIC-8, MSOP-8 |
| AD8021 | 5 to 24 | 490 | 120 | 1000 | 10,500 | SOIC-8, MSOP-8 |
| AD8038 | 3 to 12 | 350 | 425 | 3000 | 750 | SOIC-8, SC70-5, SOT-23-5 |
| ADA4899 | 5 to 12 | 600 | 310 | 35 | 100 | LFCSP-8, SOIC-8 |
| AD8057 | 3 to 12 | 325 | 850 | 5000 | 500 | SOT-23-5, SOIC-8 |
| AD8058 | 3 to 12 | 325 | 850 | 5000 | 500 | SOIC-8, MSOP-8 |
| AD8061 | 2.7 to 8 | 320 | 650 | 6000 | 350 | SOT-23-5, SOIC-8 |
| AD8062 | 2.7 to 8 | 320 | 650 | 6000 | 350 | SOIC-8, MSOP-8 |
| AD9631 | ±3 to ±6 | 320 | 1300 | 10,000 | 7000 | SOIC-8, PDIP-8 |
