AN-159: Measuring 2nV/√Hz Noise and 120dB Supply Rejection on Linear Regulators
The Quest for Quiet
Introduction
A quiet, well regulated supply is important for optimum performance with a number of circuit applications. Voltage controlled oscillators (VCOs) and precision voltage controlled crystal oscillators (VCXOs) respond to small changes in their supply very quickly. Phase-locked loops (PLLs) require a stable supply as signal on the supply translates directly to phase noise in the output. RF amplifiers require quiet supplies as they have little to no ability to reject supply variations and regulator variation will appear as unwanted side bands and lower the signal-to-noise ratio. Low noise amplifiers and analog-to-digital converters (ADCs) do not have infinite supply rejection and the cleaner the regulator output is, the higher their performance. These are just a few applications where linear regulators are required to provide quiet power supply rails, but how does one ensure that the regulator is performing as advertised?
Once fully built, one can determine if the supply being used has low enough noise for the application. Oscillator phase noise is measured and compared against results achieved with a known good supply, ADCs are checked to make sure that they are getting the maximum number of bits. These are tricky, time consuming measurements and it would be better to make sure the noise levels are low enough for your needs without expensive trials.
In addition to noise, one must also consider the supply rejection capabilities of the linear regulator. Poor rejection from a linear regulator will bring switching regulator residue or other unwanted signals through, corrupting the hard work done to ensure a clean supply. Extremely low noise from the regulator is worthless if poor supply rejection brings enough signal through to swamp noise levels.
Measuring Output Voltage Noise
Being Quiet is Nothing New
The subject of noise has been broached before. Linear Technology Application Note 83, “Performance Verification of Low Noise, Low Dropout Regulators,” published in March of 2000, describes in detail a method for measuring output voltage noise of regulators down as low as 4µVRMS with confidence. The amplifier circuit and filters in the Application Note gave 60dB of gain across a 10Hz to 100kHz bandwidth. This is a good starting point to determine confidence in measurement of noise levels. New linear regulators such as the LT3042 are now in production with much lower output voltage noise levels.
While the family of regulators released around the publication of Application Note 83 operate with approximately 20µVRMS noise in the 10Hz to 100kHz band, the LT3042 is now available with noise levels as low as 0.8µVRMS across the same frequency band. Reviewing the circuit from Application Note 83 shows an input referred noise floor of 0.5µVRMS, which provides less than 1% error when measuring noise levels as low as 4µVRMS. With output noise levels of 0.8µVRMS, this noise floor is now unacceptable; the regulator itself operates at noise levels only slightly above the measurement circuit. This translates to almost 20% error, making the measurement circuit too significant a factor to be able to measure signals with confidence.
Measuring less than 1µVRMS noise is not a trivial task. Working backward from a 10Hz to 100kHz measurement band, this equates to a noise spectral density of 3.16nV/√Hz (assuming white noise). This is equivalent to the Johnson noise of a 625Ω resistor! Measuring noise at these levels within 5% requires that instrumentation have an input referred noise of 1nV/√Hz; measuring within 1% requires input referred noise of 450pV/√Hz.
What Measurement To Make?
We now have an idea of the noise floor required by instrumentation, but there is a question as to what frequency range is critical and what instrument is to be used to measure the resultant noise. To measure noise spectral density, the regulator output can simply be fed through low noise gain stages1 and then fed into a spectrum analyzer, blocking out unwanted frequencies from measurement. If peak-to-peak or RMS noise is desired, then band stops.
are warranted on the low noise gain stages to ensure that only signal in the desired bandwidth is measured. A commonly used broadband noise measurement frequency range is 10Hz to 100kHz. This encompasses the audio frequency band and ensures minimal side bands for baseband data transmitted over RF. Low noise regulators used in phase-locked loops and high accuracy instrumentation require higher frequency measurements (up to 1MHz and beyond), so we should not limit ourselves to only the 100kHz range. Ideally, band stops would be absolute brick-wall filters at the desired frequency, but the realities of circuit design prevent us from achieving this. Higher order Butterworth filters are selected to maintain maximum flatness in the range of the frequencies of interest as well as their ability to give a better brick-wall approximation. The order of the filter is determined by the error introduced by their equivalent noise bandwidth (ENB): a second-order low pass Butterworth has an ENB of 1.11fH, too high of an error. Fourth-order filters drop the ENB to 1.026fH, which gives error levels of approximately 1.3%. Higher order filters would add unnecessary complexity and cost while accomplishing minimal improvement in performance. Fourth-order filter error is coupled with errors introduced by the input referred noise, indicating that a measurement within 5% requires that input referred noise of the amplifier be targeted to contribute no more than 1% maximum error.
Circuit gain must be considered as well. If the gain is too low, noise of the measurement device will sum in and corrupt measurements the same as input noise of the amplifier. At the same time, instrumentation may not be sensitive enough to provide reliable results. For RMS noise measurements, an HP3400A RMS voltmeter has a bottom range of 1mV, so 60dB is an absolute minimum gain. Based on the noise floor of spectrum analyzers currently commercially available (and available from the secondary market), it was decided that 80dB would work best.
Regulator Measurement Considerations
A block diagram of the noise measurement circuit is shown in Figure 1. Initial DC blocking is followed by an ultralow noise gain stage to amplify the input by AV = 25. Following this is a 5Hz single order high pass to another gain block with AV = 20. This is followed by a 10Hz second-order Sallen-Key filter and one last stage of gain at AV = 20 bringing net gain to 10,000, or 80dB. This is followed by one of three selectable outputs depending on the high end frequency desired; available are a 1MHz limit, the 100kHz band stop discussed earlier, and a wideband output that operates to the limits of the gain stages used (the –3dB frequency is measured at 3MHz). Each output is followed by one last 5Hz high pass filter to block any residual DC.

Figure 1. Filter and Gain Sections for Noise Testing. Butterworth Sections Provide Appropriate Response for Frequency Range.
The actual circuit follows in Figure 2. Here, the DC blocking is shown as a 680µF capacitor followed by a 499Ω resistor. The capacitance and resistance values chosen are one of the major trade-offs in the circuit. The resistor must be low enough in value so that the base currents of the following stage will not cause significant DC error. But if too low a value is chosen, the capacitance required in the filter becomes extremely large. A low resistor value also may allow the filter to become part of the frequency compensation for the regulator under test, changing the results measured. The current values form a 0.5Hz high pass filter.

Figure 2. Implementation of Figure 1. Low Noise Transistor Differential Pairs with Stages Paralleled to Reduce Noise While Providing Gain.
The architecture of the first gain stage is critical. This stage must provide fixed gain while operating with extremely low input referred noise. Based on previous work done by the late Jim Williams in AN124, “775 Nanovolt Noise Measurement for A Low Noise Voltage Reference,” a differential transistor pair driving the inputs of an op amp was chosen to give best bandwidth while still providing low noise. Operating the differential pair at a gain of approximately 80 means that the noise of the transistors dominates and op amp noise is not a significant factor.
The ultralow noise amplifier first stage is formed by two matched pairs of THAT300 transistors in parallel (to lower input-referred noise) followed by an LT1818 configured to give a total gain for the stage of 25. The THAT300 transistors come as four devices in a single SO-14 package and offer good matching characteristics (typical 500µV ∆VBE) and typical 800pV/√Hz noise. The LT1818 was chosen for the high gain-bandwidth product.
Paralleling of input pairs and amplifier stages provides a benefit in terms of noise floor without sacrificing gain. Amplifier circuits are known to show a drop in voltage noise when paralleled, with N stages giving a √N reduction in noise. Paralleling of the transistor pairs lowers the effective noise back to 800pV/√Hz. This noise is then further reduced by paralleling four of the full input stages together for another noise reduction of 2X to 400pV/√Hz. Subsequent addition of noise sources is minimal, allowing us to be close to the 450pV/√Hz desired for 1% accuracy.
Following the first stage, 330µF capacitors and 100Ω resistors provide DC blocking of any offsets that are inherent to the differential transistor pair and op amp. These also provide a 5Hz highpass filter, helping to create the desired low frequency band stop. All four input stages are summed together into a second stage with a gain of 20. As the input has already been amplified at this point, the op amp noise is again a small factor.
The 10Hz second-order high pass is a simple unity-gain Sallen-Key filter; an increase in the Q of this filter is used to help offset the frequency response of the single 5Hz highpass stages and give a 3dB point of 10Hz for the total circuit. Again, the DC blocking of this stage prevents any offsets that may have been amplified in the previous stage from being subjected to additional gain. Failure to block DC between various stages could lead to driving amplifiers to the rails and invalidating measurements. Each stage of gain has been interspersed with a filter to prevent DC from getting through while providing the low end band stop at the same time.
The last stage is a simple inverting amplifier with adjustable gain to compensate for variations in component values. From here, the circuit splits into three output stages. The highest bandwidth comes straight from a follower avoiding low pass filtering, giving the maximum 3MHz bandwidth for noise throughput at full gain. The second output has a 1MHz fourth-order Butterworth low pass filter, and the final output features a 100kHz fourth-order Butterworth low pass filter. All three stages use one final DC blocking RC filter at 5Hz.
Component Choice is Important
Choosing the right components for any circuit is important, but when it comes to ultralow noise measurement, it becomes even more so. The most critical point in the noise amplifier is the input stage; once you get beyond this first stage many of the difficulties drop away. The RC filter used for DC blocking directly at the input must be carefully considered.
The resistor is not one where there is much to debate; a metal film resistor is used to ensure low 1/f noise as compared to thin film resistors. The capacitor is another matter entirely that must be reviewed. In AN124, an expensive wet slug tantalum was used to provide low 1/f noise after being hand-selected for low leakage. When operating as low as 0.1Hz, these characteristics are more important. With a 10Hz low frequency band stop for broadband noise, lower cost capacitors provide acceptable performance. Large multilayer ceramic capacitors are a poor choice as they are piezoelectric in nature; any mechanical vibration injects signal into the circuit that quickly exceeds the measured noise levels. Additionally, the voltage coefficient causes a change in the corner frequency based on the regulator output voltage, an undesirable characteristic. Tantalum and aluminum electrolytic capacitors are not costly and do not show voltage coefficients or mechanical sensitivity. More expensive capacitors such as polyethylene-terephthalate film were considered, but low availability, high cost, and lack of performance gain ruled them out.
Even with these possible choices, capacitors do show noise characteristics that must be considered. Large multilayer ceramic capacitors show low noise operation but have already been ruled out due to their mechanical vibration sensitivity. Tantalum and aluminum electrolytic capacitors show higher levels of noise (see Sikula, et al. in References for further reading). Standard tantalum capacitors were finally chosen for their reasonable cost, good characteristics with bias voltage, and lack of response to physical vibrations. Multiple capacitors are paralleled to get the voltage rating and net capacitance needed, while lowering the contributed noise.
The blocking/filtering between first stage gain blocks and the second stage gain block was also chosen to be tantalum for similar reasons. Even though the gain from the first stage amplified the noise, ceramics were found to generate signal from piezoelectric response beyond desired levels.
Almost any capacitor is suitable for the final output blocking/filtering networks, ceramic capacitors are chosen. The amplified noise is now large enough in relation to piezoelectric response from the capacitors, and the lack of DC offset means that capacitors are close to their expected values. Capacitors for compensation in the first gain stage and also the ones used in the Butterworth filters are C0G, NPO, or polyethylene-terephthalate as these dielectrics show little to no piezoelectric effect or DC bias shifts.
Powering the circuit itself is one last important decision. Battery power from alkaline cells was chosen to provide the quietest source for all stages and prevent possible ground loops in equipment from corrupting measurements. One must remember that all circuits used here do not have infinite supply rejection capabilities and any noise on supplies can make it through to the outputs and potentially affect measurement results. Take this into careful consideration before choosing to supply power from any line-based supply.
Practical Circuit Limitations
The amplifier has practical limitations that cannot be ignored. Given the 80dB of gain provided by the circuit, a signal on the input of 100µVP-P will show as 1VP-P on the output. Running from ±4.5V supplies dictates an output signal is less than ±3.5V in amplitude. Thus, the input cannot see more than ±350µV total amplitude or signal fidelity cannot be guaranteed. Expecting a worst-case crest factor of 10 for Gaussian noise, only 70µVRMS maximum is measurable with this circuit.
From here, making sure the tantalum capacitors are properly biased is also important. For the input blocking capacitor, the transistors are operating almost at ground potential, so a positive output voltage regulator requires that the positive side of the capacitor be connected to the regulator output. Contrarily, the capacitor is reversed when measuring a negative output voltage. For the DC blocking and filtering between the first and second stages, the negative side of the capacitor should be connected to the first stage. Base current of the transistors pulls their bases slightly negative through the 499Ω resistor, and this slightly negative voltage is amplified further through the gain of 25 in the first stage, requiring this orientation.
Calibration, Verification, and Measurement
Once the circuit is built, the gain needs to be verified as well as the input-referred noise. To calibrate gain, 60dB attenuation2 is used to bring the signal from a function generator down to a level that avoids running the amplifier output against the rails. With 100mVP-P at a midrange frequency of 1kHz from the function generator into the attenuator, the potentiometer in the final gain stage is adjusted to give 1VP-P at the output. Adjusting the frequency up and down from 10Hz to 1MHz gives indication that the gain is flat across the desired bandwidth.
Verification of gain and frequency response is done with a network analyzer. The reference signal is fed through the 60dB attenuator into the input of the amplifier. The three separate outputs are connected as the test point, and sweeps across frequency are made. Figure 3 shows the gain as a function of frequency for each of the three outputs, highlighting the excellent flatness and appropriate corner frequencies.

Figure 3. Gain of Circuit in Figure 1. Filter Responses Show Steep Roll-Off at Desired Corner Frequencies.
To verify input-referred noise, short the input of the amplifier to ground and measure the noise at the output. Measurements are taken directly with an RMS voltmeter or oscilloscope; noise spectral density is viewed with a spectrum analyzer. Measured noise spectral density of the wideband output (shown in Figure 4) has 1/f noise with a corner at 200Hz, and white noise characteristics of 5µV/√Hz from 200Hz to 1MHz. Dividing this down by the gain of 80dB indicates input-referred noise is 500pV/√Hz, slightly above the target. Even with the 1/f component, this calculates to 0.15µVRMS over the 10Hz to 100kHz bandwidth, low enough to allow measurement of 1µVRMS over the same bandwidth with confidence. The measurements correlate well with the peak-to-peak noise measured on an oscilloscope as shown in Figure 5.

Figure 4. Noise Spectral Density of Amplifier with Input Shorted Shows 1/f Component. Dividing by 80dB Circuit Gain Yields Input Referred Noise.

Figure 5. Peak-to-Peak Amplifier Noise with Input Shorted (100kHz Range) Correlates to Noise Spectral Density.
Measurements Are Still Not a Simple Task
Several subtle effects cropped up during the design and testing of this circuit that showcased the difficulty in measuring ultralow noise levels. Shorting the input to ground and connecting the output to an oscilloscope reveals much that cannot be seen with an RMS voltmeter or spectrum analyzer. Large signal excursions when using ceramic capacitors for the input filter and second stage filtering showcased their piezoelectric nature from simple finger taps on the bench. This made the case for the switch to solid tantalum capacitors.
What was also apparent was that the noise levels for measurement were so small that extraordinary measures were required to ensure solid results. Placing the amplifier board in front of an older oscilloscope showed a regular 20kHz signal (likely a switching regulator inside the oscilloscope) that was larger in amplitude than the input referred noise. Placing it close to a benchtop multimeter resulted in a large 60Hz signal. Figure 6 shows just how sensitive the amplifier is when placed just a few inches in front of the powered oscilloscope. In both cases, moving the board away from the equipment or changing the orientation of the board would change the amplitude of the signal and turning the equipment off would remove the signal. A few loops of wire around the end of a pencil were connected to a function generator to operate as a small antenna at various frequencies. Not surprisingly, some areas of the board showed circuit loops that were magnetically coupling with the inductors and transformers inside the bench equipment. Some layout improvements were made to help minimize loops, but it was immediately obvious that external shielding would be required.

Figure 6. Signal Shown with Input Shorted and Close to Oscilloscope Highlights Sensitivity to Magnetic Fields.
Shielded Box Construction
Figures 7 and 8 show the internal construction of the shielded box used to house the noise amplifier board. The amplifier board is housed together with six D cell alkaline batteries inside a box constructed from 0.050" thick Mu Metal to give good shielding against low frequency magnetic fields. This is then placed 1/2" inside a box made from 2oz. copper clad, chosen to give good shielding against higher frequencies. These are lastly placed 1/2" inside a steel can (a repurposed cookie tin3) that gives some initial shielding from magnetic fields. The 1/2" air gaps between boxes help with attenuation of fields. For a discussion on materials useful for low frequency magnetic field shielding, please see Appendix A, Materials for Magnetic Shielding.

Figure 7. Shielded Box Construction Uses Mu Metal Inside Copper Inside Steel Tin to Attenuate Fields.

Figure 8. Details of Shielded Box Construction. Note Only Input Coax Shield is Connected to Metal Can to Prevent Ground Loops.
There are a few worthwhile items to note about the construction of this box. The internal amplifier board uses coaxial cable to go from the board out to the input and output BNC connectors. However, one must watch connections for the shield of the coaxial cables; only the input shield is connected to the ground plane of the board and the outermost steel can. Input and output BNC shields connect to the steel can, while coaxial cable shields tie to the board ground on both sides. If the output shield connections were to be connected to the steel can as well, a ground loop is formed that can pick up stray fields. Each layer of the shielding box electrically connects to the one outside it via metal screws and standoffs with the amplifier board isolated by solder mask. These provide connections between each box without connecting to the ground plane of the amplifier board internally and creating possible loops. Last, the steel can itself is given added attention: the inside and outside edges of the can and lid were sanded to remove the decorative paint and clear protective layers to ensure good electrical contact between the lid and can.
It is worth noting that even with all of the attention paid to shielding the circuit, line frequency fields are strong enough to make their way into the noise plot shown in Figure 4. Fortunately, the shielding is enough to minimize signals created by these fields. Even so, one should be fully aware of the potential for fields to interact with this circuit when making measurements.
Measuring Regulator Output Noise
Once the amplifier is checked and calibrated, actual noise measurements are made. Accurately measuring linear regulator output noise and obtaining faithful results requires careful attention to DUT shielding, component choice, layout, and cable management. Figure 9 shows the configuration used for testing a linear regulator, highlighting the construction and shielding used to avoid magnetic fields from intruding on the measurement. Only one instrument is connected at any given time to preclude ground loops from corrupting the measurement.

Figure 9. Noise Measurement Bench Setup. Shielded Box Houses Noise Amplifier, Low Output Impedance of Linear Regulator Removes Necessity for Shielding, but Magnetic Fields Can Still Affect Output.
Battery power is chosen to supply the linear regulator for the same reason as powering the amplifier; the goal is to measure the noise of the linear regulator, not characterize supply rejection. The regulator does not need to be shielded, as the low output impedance of the regulator makes it much less susceptible to low frequency magnetic fields. Connections from the regulator output to the noise amplifier need to be short barrel connectors since long flexible cables will introduce errors due to triboelectric4 effects.
The amplifier output is fed directly into an oscilloscope to measure peak-to-peak noise. As shown in Figure 10, the peak-to-peak noise of the LT3042 is 4µVP-P. A spectrum analyzer plot of the same regulator (shown in Figure 11) shows the noise for various amounts of SET pin capacitance. The RMS noise from 10Hz to 100kHz as a function of SET pin capacitance is shown in Figure 12.

Figure 10. LT3042 Noise in 10Hz to 100kHz Bandwidth. RMS Noise Measures 0.8µVRMS.

Figure 11. Noise Spectral Density Plot Shows Effect of Increasing SET Pin Capacitance on LT3042.

Figure 12. Increasing SET Pin Capacitance Decreases RMS Noise in 10Hz to 100kHz Bandwidth.
Measuring RMS noise requires one to be more fastidious in selecting instrumentation. All RMS voltmeters are not created equal, please review Appendix C, Understanding and Selecting RMS Voltmeters, from AN83, “Performance Verification of Low Noise, Low Dropout Regulators,” for information on types of RMS voltmeters and their performance. This appendix lists many different RMS voltmeters and highlights how some have significant errors, leading to measurements that are more optimistic than reality.
Measuring Regulator Supply Rejection
Just as Important as Noise
Supply rejection for a linear regulator is just as critical as output voltage noise. With poor supply rejection, even the lowest noise regulator will pass signal through to the output, and this can swamp the noise from the regulator. Switching regulators are often employed as preregulators to provide an optimal combination of efficiency, noise, transient response, and output impedance.
Most state-of-the-art switching regulators operate at frequencies from 100kHz to 4MHz. Even with the lowest ESR capacitors, the pulsed nature of energy transfer that defines switching regulators creates output voltage ripple at the switch frequency. These signals cause problems in noise-sensitive video, communications, and other types of circuitry. This has been touched on in Linear Technology Application Note 101, “Minimizing Switching Regulator Residue in Linear Regulator Outputs,” published in July of 2005.
Recently released linear regulators are promising supply rejection in the range of 80dB and above. The LT3042 approaches 120dB of supply rejection at certain frequencies. For testing this, the input must be kept at a low enough amplitude to ensure the small signal response of the regulator is tested as opposed to large signal response, although enough signal must be generated to have a measurable signal at the output. Additionally, the input DC level with the superimposed AC signal must not drive the regulator into dropout or other unwanted operation regions.
Driving the DUT
When testing regulator rejection, the first thing that must be done is to supply a signal to be rejected. This is more complex than just connecting a frequency generator to the device; the AC signal must ride on top of a DC offset and be capable of providing the current required under load.
The circuit used for this purpose was developed by Jim Williams and is shown in Figure 13. In this circuit, a DC reference voltage is generated by A2 and summed with an AC signal on the inverting input of A1. The output of A1 drives Darlington connected transistors that are paralleled with ballast resistors to drive up to 5A output current.

Figure 13. Driver Board Sums AC and DC Voltages to Provide Several Amps at Frequencies to 10MHz.
One major caveat needs to be noted when connecting this circuit to the DUT: input capacitance for the regulator should not be used. The first reason is that the circuit is not optimized for driving capacitive loads and may oscillate. Second, there is no ability for this circuit to sink current; a load must be present to discharge input capacitors, especially as frequency increases. Driving a 50mVP-P sinusoidal signal at 10MHz across a 1µF capacitor requires over 3A of charge and discharge current to prevent signal distortion. If making measurements at light output currents (under 100mA), use a preload to ensure signal fidelity presented to the regulator.
Thinking Ahead
When a device presents very high supply rejection, careful attention must be paid to the details of the instrumentation. If the regulator provides 100dB of supply rejection, a 50mVP-P input signal is reduced to 0.5µVP-P at the output. Increasing the input signal amplitude is possible, but at some point a transition from small signal response to large signal will occur.
For a regulator with high supply rejection, the low amplitude of the output signal is comparable to or smaller than the amplitude of the noise of the device. This suggests that we should amplify the signal much the same that we did for the noise to be able to make accurate measurements. Even with this, the output signal is often hidden by the noise. Fortunately, modern oscilloscopes provide averaging capabilities that allow one to extract the signal from the noise; the average value of random noise is zero. The input signal supplies the trigger needed.
Whether or not the signal is amplified, other possible issues arise when measuring supply rejection. The input and output signals must be measured simultaneously; one needs both input and output amplitudes to know the rejection of the device. A block diagram of the measurement setup is reviewed in Figure 14.

Figure 14. Block Diagram of Supply Rejection Measurement Shows Ground Loops. Switching to Differential to Single-Ended Amplifier Resolves Ground Loops.
Worth noting in the block diagram is that ground loops exist that can corrupt the measurement. The first is the ground loop formed through the common ground of the two oscilloscope channels. This loop passes through the signal amplifier and any signal in the ground loop corrupts the supply rejection measurement, giving results that do not reflect actual performance. The solution to this is to switch the signal amplifier from a single-ended circuit to fully differential. In doing so, both loops are broken and measurement fidelity returns. The second loop (not shown on Figure 14) comes through the AC line ground to the first oscilloscope channel. This loop shows minimal contribution to errors as all signals are large in comparison.
Simple Amplifier for Differential Inputs
A simple amplifier is shown in Figure 15. This amplifier uses a fully differential gain stage on the input with a gain of 40dB followed by a differential to single-ended converter to give another 20dB of gain. Each input has a 200Hz highpass filter to block DC. The LTC6409 was chosen for its high gain-bandwidth product of 10GHz. The second stage is provided by an LT1818 configured as a differential to single-ended converter with a gain of 20dB.

Figure 15. Simple Differential to Single-Ended Amplifier Provides 60dB of Gain.
The input referred noise of this combination of amplifiers runs approximately 1.4nV/√Hz, which means that we should expect less than 2.2µVP-P of noise. At the same time, we expect 4µVP-P of noise from the regulator itself. Compared to the 0.5µVP-P of signal we are expecting at the output of the regulator, this noise completely swamps the signal we are trying to measure. Again, the saving grace is the random nature of noise giving an average value of zero: using a modern oscilloscope with memory, averaging reveals the signal hidden within the noise.
Improved Differential Amplifier
Measurements from extremely high performing linear regulators get even trickier. With only 60dB of gain on the output signal, a 0.5µVP-P signal becomes 0.5mVP-P. This small amplitude is approaching the measurement thresholds of many high end oscilloscopes with 1X probes. Increasing the input amplitude to the linear regulator tenfold gives added headroom, but if regulator supply rejection increases another 20dB, then the problem once again rears its head.
Figure 16 shows the implementation of a higher performance amplifier. It is based on both the noise amplifier of Figure 2 and the previous differential to single-ended amplifier in Figure 15. Now, the LT1818 used for each stage is replaced with LT1994 differential amplifiers that feed back to the differential transistor pairs, still formed by the THAT300 transistor arrays. A second stage of differential gain comes from another LT1994 before being converted to single-ended measurement through the first LT6232. Successive stages for highpass and Butterworth filters follow those in Figure 2. Calibration and verification of circuit response is the same as the low noise amplifier.

Figure 16. Improved Amplifier Provides Differential Inputs with 80dB of Gain.
The setup to measure supply rejection is shown in Figure 17. Measured supply rejection of the LT3042 regulator is shown in Figure 18. It is worth noting that the supply rejection of the regulator approaches 120dB at 100Hz. Verification of this measurement on an oscilloscope necessitates the 80dB of gain from the improved amplifier.
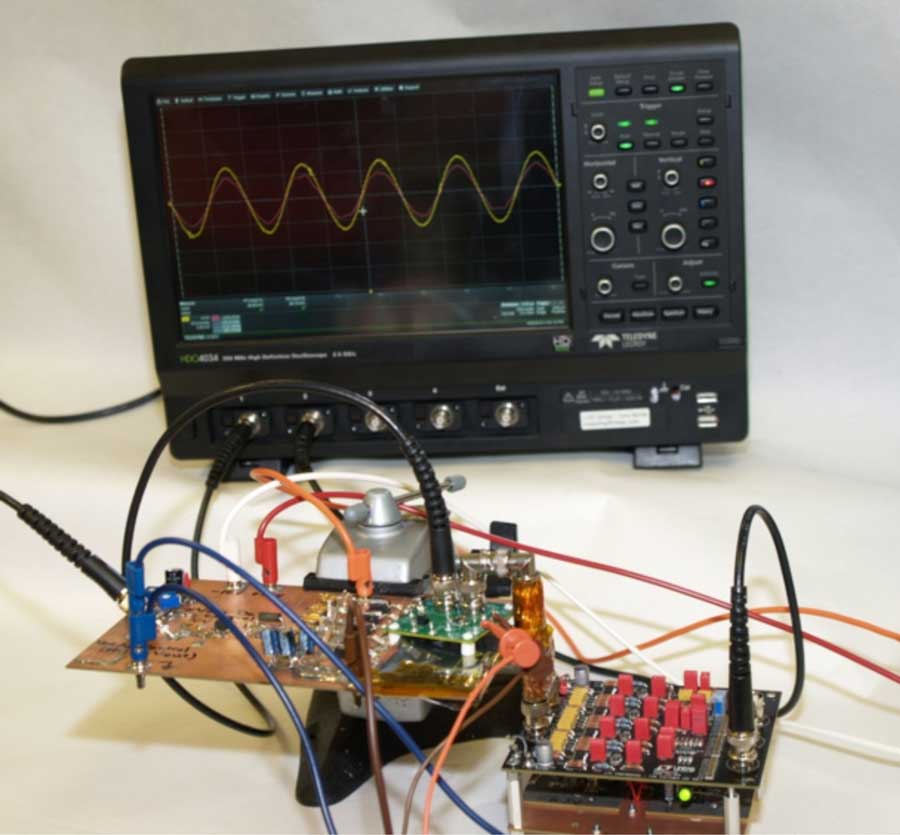
Figure 17. Setup for Measuring Supply Rejection. Driver Board and DUT on Bottom Left, Amplifier Board on Bottom Right. Power Supplies and Signal Source Not Shown.

Figure 18. Supply Rejection Plot of LT3042 Shows >70dB Performance to Frequencies Approaching 4MHz.
Other Methods for Measurement
Other methods and equipment are available to make supply rejection measurements. A lock-in amplifier uses the reference signal to provide synchronous detection at the desired frequency to help measure small signal levels.
A network analyzer also provides an oscillator to sweep across frequency while providing the bandpass function to measure both input and output amplitudes and calculate the rejection of the circuit. These methods provide valid results, but one still needs to be fastidious with circuit connections and verify results. Checking both input and output signals on an oscilloscope is a must; signal amplitudes and wave shapes will indicate if the regulator under test is being driven into dropout or if small signal response has given way to large signal behavior.
Pitfalls
Similar to measuring noise, there are pitfalls that can lead one astray when measuring supply rejection. Careful attention to circuit grounding using star grounds is important. Some effects that are seen while measuring supply rejection actually seem counter intuitive.
Up until now, a solid design would always include some capacitance at the input of the linear regulator to keep the supply impedance as low as possible across frequency. With high enough supply rejection from a device, this can actually increase the amount of ripple seen at the output.
Consider a circuit as shown in Figure 19 where the LT3042 post-regulates the LT8614 Silent Switcher® regulator. The LT8614 delivers approximately 20mVP-P of ripple at its 500kHz switching frequency to the input of the LT3042 through a couple inches of copper board traces. With only the 22µF output capacitor of the LT8614, output ripple of the linear regulator is only a few µVP-P. When a 4.7µF capacitor is added at the input of the LT3042, output ripple increases to approximately 75µVP-P, as shown in Figure 20. It should be noted that bandwidth was limited to 20MHz for these photos as the goal was to show ripple at the switching frequency, not high frequency edge spikes.

Figure 19. Using the LT3042 to Post-Regulate the LT8614 Silent Switcher.

(a)

(b)
Figure 20. The LT3042 Post-Regulating the LT8614 Silent Switcher (a) without Any Capacitor at the LT3042 Input, (b) with a 4.7μF Capacitor at LT3042 Input. Both Photos are Bandwidth Limited to Ignore High Frequency Spikes.
How is it that adding input capacitance reduces the supply rejection of the regulator? The answer lies not with the performance of the LT3042, but in the board layout. The LT3042 provides exceptional capability at electrically rejecting signals from the input supply. Up until now, the ability to reject these signals was the limiting factor. Now, magnetic fields become the culprit.
To better understand this, the schematic in Figure 21 highlights an AC current path of the DC-DC converter with a solid green line. If capacitance is present at the input of the LT3042, AC current also flows in the broken green path. The input of the LT3042 presents a high impedance at the frequency of concern, so no AC current flows into the LT3042.

Figure 21. Schematic Highlights AC Current Loop of DC-DC Converter Together with Paths Susceptible to Magnetic Coupling.
The AC current flow creates a magnetic field that will produce current in other nearby loops, the same way one winding of a transformer couples to other windings. Two loops of concern are shown in blue and red on Figure 21. The blue loop, formed by CSET and RSET, generates ripple at the input to the error amplifier. With the unity-gain architecture of the LT3042, this ripple is transferred through to the output. The red loop formed by the output capacitor and the impedance looking back into the regulator (and nearby load components as well) generates ripple directly on the regulator output.
Counter intuitively, removing capacitance from the input of the LT3042 reduces output ripple. Given that this is not electrical feedthrough of signal, but is instead magnetic coupling, one must think about distance, shielding, and loop orientation when designing boards. Field strength is related to distance and loop area, so minimizing loop area (by not using an input capacitor) and maximizing distance (by only using the DC-DC converter output capacitance) limits the current impressed on sensitive loops.
This reveals that the decision early on to not use capacitors on the output of the signal driver board or input of the regulator was prudent. With a capacitor right at the inputsof the regulator, a loop is added creating magnetic fields that couple into the output and give erroneous results. The regulator supply rejection would appear to be much worse than it actually is.
One other issue that comes to light when using switching regulators is not just removing the switch frequency ripple, but the spikes associated with the switch edges. Switch edges on some circuits are transitioning in just a few nanoseconds, translating to frequency content in the 100s of MHz. These frequencies cannot be easily eliminated with a simple linear regulator. Parasitic effects like trace capacitance and magnetic coupling make reduction of these spikes difficult. Please refer to Linear Technology Application Note 101, “Minimizing Switching Regulator Residue in Linear Regulator Outputs,” and Appendix B, Controlling High Frequency Switch Spikes, for further information.
Conclusions
The exacting performance offered by linear regulators like the LT3042 provides exceptionally quiet supply rails for sensitive systems. Verification of DC performance from such a device is usually not a tricky proposition. Critical parameters such as noise and supply rejection are not as easy to measure at such high performance levels. Careful attention must be paid to the smallest of details in measurement circuits, connections, board layout, and equipment. What were once small errors that could be ignored (compared to the signal being measured) are now firstorder error terms. The high PSRR performance delivered shows that signals are not being transmitted through the device itself, but through magnetic coupling. Every detail must be scrutinized to ensure fidelity of measurements and provide solid results that are trustworthy.
Notes
1 Of course, input referred noise on the low noise gain stages must be small enough to avoid corrupting the measurement.
2 Don’t have a 60dB attenuator? You can always make one from a 1k/1Ω resistor divider.
3 If you would like Linear Technology to verify your cookie tin for repurposing, please make certain to send it in with its original contents.
4 The triboelectric effect is when a charge is produced on the dielectric material within a cable if the dielectric does not maintain contact with the conductors. see Ott in References..
Appendix A
Materials for Magnetic Field Shielding
Aluminum and copper enclosures are commonly used for RF shielding to keep unwanted signals out of sensitive circuitry. These enclosures will not work with magnetic coupling, especially at the low frequencies seen in bench testing. A thin walled steel can (even enclosing a copper or aluminum box) will not provide enough attenuation of magnetic fields. What is needed is a material with very high magnetic permeability—the lines of magnetic flux must be diverted around the circuit instead of being allowed to go through it. Common techniques use multiple layers of materials of shielding separated by an air gap. Each subsequent layer helps attenuate the field strength as well as providing some distance between layers for further reduction. The problem lies in trying to look at magnetic permeability of materials and determine the thickness and configuration needed to shield the circuit adequately from fields. A simple steel enclosure would require extremely thick walls (estimates are at least 1/2" wall thickness) in order to provide adequate shielding. This would require a custom steel box welded together, one that would most likely never move once placed on a bench due to the weight involved. Depending on the alloy, steel has a relative magnetic permeability between 400 and 2000, while copper and aluminum are very close to 1.
Materials with extremely high magnetic permeability became a requirement for shielding. High nickel alloys such as Mu Metal offer a relative magnetic permeability of 20,000 ranging to 50,000 when properly annealed after forming. Testing chambers are available from Mu Metal provider Magnetic Shield Corporation that are three nested cylinders; one places sensitive circuitry inside to avoid magnetic coupling issues. These chambers are expensive, but are a simple solution to provide magnetic shielding. If you do not have an issue with creating your own enclosure, sheets of Mu Metal are available for purchase for cutting and forming to custom shapes. Thicker sheets are recommended for best shielding to avoid saturation of the material and magnetic field incursion. Be aware that the relative magnetic permeability will drop during forming and the material must be properly annealed afterwards in a hydrogen-rich atmosphere.
Another possible material is an amorphous metal alloy called Metglas. Metglas arrives in two inch wide ribbons that are 0.8 mils thick. It is not available in large sheets to cut and form into enclosures as is Mu Metal. It is used by wrapping the ribbon around the board with the overlap being enough to prevent unwanted fields from getting through; magnetic fields tend to penetrate to a depth of only twice the diameter of any hole in the material. Metglas offers much higher levels of relative magnetic permeability than Mu Metal depending on the alloy. Metglas 2705M was tried as it gives an as cast relative magnetic permeability of 290,000 without needing special annealing techniques in a hydrogen-rich atmosphere. If an annealing chamber is available, Metglas 2714A offers a relative magnetic permeability that reaches 1,000,000. The issue found with the use of Metglas for shielding lies in the 0.8 mil thickness; the thin ribbon is easier to saturate and multiple layers are required for effective shielding.
Appendix B
Controlling High Frequency Switch Spikes
Some of the latest switch-mode power supply circuits have much faster switch transition times compared to previous generations. The faster transitions have benefits that be seen in improved efficiency and smaller external components among others. The difficulty with these faster edges comes in minimizing the associated spikes that make their way onto and into sensitive circuitry.
Switch transition times have sped up, with harmonic content going from the tens of MHz to frequencies now approaching 1GHz. Designers in the RF realm will appreciate the difficulty in wrangling these signals. At such frequencies, component parasitics dominate, traces become transmission lines, and antennas now exist that transmit and receive energy around the board. There are two ways that high frequency content is injected into the output of a linear regulator: conducted and magnetically coupled. Treating the problem in the RF realm provides the best results in taming the issue.
Conducted signals make their way through the regulator and onto the output. The linear regulator itself cannot actively reject any of these signals; the unity-gain bandwidth of the regulator is usually a maximum of 1MHz. The regulator has a parasitic capacitance from input to output that allows high frequency content to propagate through. Parasitic inductance and resistance degrade the effectiveness of output capacitors at these frequencies.
The best way to control conducted spikes is through the use of ferrite beads on the input of the regulator. In the frequency range where the regulator is active, the ferrite bead provides a low loss path. As frequency rises above this range, the bead increases in impedance, limiting the high frequency energy passed through.
Controlling the paths for radiated signals to make their way to the output requires attention to detail the same as with conduction paths. Ferrite beads will not prevent radiated energy from coupling onto the output of the regulator. Shielding offers a good way to help minimize high frequency radiated content from coupling onto the linear regulator output. Additionally, providing separation from components that see high frequency signals reduces field strength.
Thinking about both paths for high frequency signals to make their way onto the output will provide best results in creating a quiet supply for sensitive circuitry. A combination of ferrite beads, shielding, and distance will offer optimum overall rejection. The linear regulator and its output capacitor should be shielded with an appropriate material and placed physically away from the hot loop of the switching supply. The input capacitor of the linear regulator should be located close to the switching supply instead of next to the linear regulator. Two to three inches of distance is enough to reduce the fields associated with the AC currents through the capacitor. Lastly, a ferrite bead should be placed between the switching supply and the regulator. The ferrite bead is placed between the input capacitor and the regulator without deleterious effects. Figure B1 shows a schematic of how to connect the circuit, while Figure B2 highlights construction details.

B1. Use of Ferrite Bead, Shielding, and Physical Distance Combine to Provide Optimum High Frequency Spike Reduction.

B2. Construction of Board from Figure B1.
参考資料
1. Morrison, Ralph, “Grounding and Shielding Techniques in Instrumentation,” Wiley-Interscience, 1986.
2. Ott, Henry W., “Noise Reduction Techniques in Electronic Systems,” Wiley-Interscience, 1976.
3. THAT 300 Series Data Sheet, THAT Corporation.
4. Williams, Jim, “775 Nanovolt Noise Measurement for A Low Noise Voltage Reference,” Linear Technology Corporation, Application Note 124, July 2009.
5. Williams, Jim and Owen, Todd, “Performance Verification of Low Noise, Low Dropout Regulators,” Linear Technology Corporation, Application Note 83, March 2000.
6. Patel, Amit, “Industry’s First 0.8µVRMS Noise LDO Has 79dB Power Supply Rejection Ratio at 1MHz,” Linear Technology Journal of Analog Innovation, April 2015, pp. 1-7.
7. Williams, Jim, “Practical Circuitry for Measurement and Control Problems,” “Symmetrical White Gaussian Noise” Appendix B, Linear Technology Corporation, Application Note 61, August 1994, pp. 38-39.
8. Williams, Jim, “Minimizing Switching Regulator Residue in Linear Regulator Outputs,” Linear Technology Corporation, Application Note 101, July 2005.
9. Metglas 2705M Technical Bulletin, Metglas, Inc.
10. Metglas 2714A Technical Bulletin, Metglas, Inc.
11. ZG-2 Brochure, Magnetic Shield Corporation.
12. Mu-2 MuMETAL Brochure, Magnetic Shield Corporation.
13. Sandler, Steven and Hymowitz, Charles. “Capacitor Values: Don’t Believe the Label,” Power Electronics Technology, May 2007, pp. 22-27.
14. Sikula, J., J. Hlavka, J. Pavelka, V. Sedlakova, L. Grmela, M. Tacano, and S. Hashiguchi. “Low Frequency Noise of Tantalum Capacitors.” Active and Passive Electronic Components 25.2 (2002): 161-67. Web.
15. Kueck, Christian, “Power Supply Layout and EMI,” Linear Technology Corporation, Application Note 139, October 2012.
