Noise Analysis of Precision Data Acquisition Signal Chain
In many applications, the analog front end takes either a single-ended or differential signal and performs gain or attenuation, antialiasing filtering, and level shifting as required and then drives the inputs of the ADC at the full-scale level. This article gives insight into noise analysis of the precision data acquisition signal chain and takes a deep dive to figure out the overall noise contribution from this signal chain.
As shown in Figure 1, the low power, low noise, fully differential amplifier, ADA4940-1, drives the differential inputs of the AD7982, 18-bit, 1 MSPS PulSAR® ADC, while the ADR435, low noise, precision 5 V reference is used to supply the 5 V needed for the ADC. This signal chain eases analog signal conditioning by eliminating the need for an extra driver stage and reference buffer, which results in board space and cost savings. A single-pole, 2.7 MHz, RC (22 Ω, 2.7 nF) low-pass filter is placed between the ADC driver output and the ADC inputs to help limit the noise at the ADC inputs and reduce the effect of kickbacks coming from the capacitive DAC input of a successive approximation register (SAR) ADC.

Figure 1. Low power, fully differential, 18-bit, 1 MSPS data acquisition signal chain (simplified schematic: all connections and decoupling not shown).
When used as an ADC driver, the ADA4940-1 allows the user to do the necessary signal conditioning, including level shifting and attenuating or amplifying the signal for more dynamic range using four resistors. This eliminates the need for an extra driver stage. The ratio of feedback resistors (R2 = R4) to gain resistors (R1 = R3) sets the gain, where R1 = R2 = R3 = R4 = 1 kΩ.
For a balanced differential input signal, the effective input impedance would be 2× the gain resistor (R1 or R3) = 2 kΩ, and for an unbalanced (single-ended) input signal, the effective impedance would be approximately 1.33 kΩ using the equation
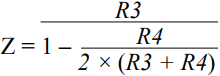
A termination resistor in parallel with the input can be used if required.
The ADA4940-1internal common-mode feedback loop forces common- mode output voltage to equal the voltage applied to the VOCM input and offers an excellent output balance. The differential output voltage depends on VOCM when two feedback factors β1 and β2 are not equal and any imbalance in output amplitude or phase produces an undesirable common-mode component in the output and causes a redundant noise and offset in the differential output. Therefore, it’s imperative that the combination of input source impedance and R1 (R3) should be 1 kΩ in this case (that is, β1 = β2) to avoid the mismatch in the common-mode voltage of each output signal and prevent the increase in common-mode noise coming from the ADA4940-1.
As signals travel through the traces of a printed-circuit board (PCB) and long cables, system noise accumulates in the signals and a differential input ADC rejects any signal noise that appears as a common-mode voltage.
The expected signal-to-noise ratio (SNR) of this 18-bit, 1 MSPS data acquisition system can be calculated theoretically by taking the root sum square (RSS) of each noise source—ADA4940-1, ADR435, and AD7982.
The ADA4940-1offers low noise performance of typically 3.9 nV/√Hz at 100 kHz as shown in Figure 2.

Figure 2. ADA4940 input voltage noise spectral density vs. frequency.
It is important to calculate the noise gain of the differential amplifier in order to find its equivalent output noise contribution.
The noise gain of the differential amplifier is:

where
![]()
and
![]()
are two feedback factors.
The following differential amplifier noise sources should be taken into account:
Since the ADA4940-1 input voltage noise is 3.9 nV/√Hz, its differential output noise would be 7.8 nV/√Hz. The ADA4940-1 common-mode input voltage noise (eOCM) is 83 nV/√Hz from the data sheet, so its output noise would be
![]()
Noise from the R1, R2, R3, and R4 resistors can be calculated based on the Johnson-Nyquist noise equation for a given bandwidth:
![]()
where kB is the Boltzmann constant (1.38065 × 10 – 23 J/K), T is the resistor’s absolute temperature in Kelvin, and R is the resistor value in ohms (Ω).
The noise from the feedback resistors would be
![]()
The noise from the R1 would be
![]()
and R3 would be
![]()
The ADA4940-1 current noise is 0.81 pA/√Hz from the data sheet.
Inverting input voltage noise:
![]()
Noninverting input voltage noise:
![]()
So, the equivalent output noise contribution from the ADA4940 would

The total integrated noise at the ADC input (after RC filter) would be
![]()
The rms noise of AD7982 can be calculated from its typical signal-to-noise ratio (SNR) of 98 dB for a 5 V reference.
![]()
Using these numbers, the total noise contribution from the ADC driver and ADC would be
![]()
Note that the noise contribution from the ADR435 reference is ignored in this case as it’s negligible.
So, the theoretical SNR of the data acquisition system can be estimated as shown below.

The AD7982 achieves typically 96.67 dB of SNR and –111.03 dB of THD for a 1 kHz input signal as shown in its FFT performance in Figure 3. The measured SNR of 96.67 dB in this case is pretty close to the theoretical estimated SNR of 96.95 dB above. The actual loss from the target SNR of the data sheet specified 98 dB is attributed to the equivalent output noise contribution from the ADA4940-1 differential amplifier circuit.

Figure 3. FFT plot, fIN = 1 kHz, FS = 1 MSPS (ADA4940-1 configured as a fully differential driver).
When selecting an ADC driver for driving the SAR ADC for a given application, noise is one important specification, as are scrutinizing the bandwidth, settling time, input and output headroom/footroom, and power requirements. For more information on recommended amplifiers for driving the high resolution precision PulSAR ADCs, refer to the Analog Devices ADC Driver Selection Guide. For designing differential amplifier circuits, download the free, intuitive, and easy to use Analog Devices DiffAmpCalc™ tool.
About the Authors
Related to this Article
Products
18-Bit, 1 MSPS PulSAR ADC in MSOP/LFCSP
Ultralow Power, Low Distortion ADC Driver
Ultralow Noise XFET® Voltage References with Current Sink and Source Capability