High performance MEMS accelerometers offer low cost solutions for a wide range of applications that incorporate inertial measurements. Some examples are navigation and AHRS systems, vibration monitoring for machine health sensing, structural health monitoring of infrastructure, and high precision inclinometers for platform stabilization, tilt monitoring in down-hole directional drilling, leveling in construction industry road graders and surveying equipment, and measuring boom angles in crane stability systems. Most of these examples subject the accelerometer to vibration spanning various amplitudes. Another aspect that varies across these applications is the frequency content of the vibration. A combination of the vibration and sensor and system error sources can lead to vibration rectification, which is an important specification for high performance accelerometers. This article describes how vibration rectification occurs in MEMS accelerometers, and discusses different techniques for measuring this parameter. As a case study, the vibration rectification of the low noise, low power accelerometer ADXL355 is discussed. The low vibration rectification error, along with all these other features, makes it an ideal candidate for the previously highlighted precision applications.

Origin of Vibration Rectification

Vibration rectification error (VRE) is the response of an accelerometer to ac vibrations that get rectified to dc, manifesting as an anomalous shift in the offset of the accelerometer. This is a significant error source in applications such as inclinometers, where the dc output of the accelerometer is the signal of interest, and any changes in the offset can be wrongly interpreted as a change in inclination, leading to a propagation of errors down the line, such as false triggering of safety systems or over compensation in platform stabilization or drill mast alignment.

VRE is highly dependent on the vibration profile experienced by the accelerometer, and it can vary from one application to the other, as the vibration patterns applied to the accelerometer vary. Vibration rectification can occur via several mechanisms, two of which will be discussed here.

Asymmetric Railing

The first mechanism is asymmetric railing. Gravity creates a static 1 g (9.8 m/s²) acceleration field that can create an offset to an accelerometer’s measurement range when the sensor axis of sensitivity is aligned vertically. A 2 g full-scale range sensor would be able to measure only 1 g peak vibrations without clipping the response when aligned with the gravity acceleration. Symmetric stimulus beyond 1 g would create a non-zero average due to the clipped level in the direction experiencing the additional 1 g of acceleration.

Figure 1 depicts a simulation of vibration signal impressed on a 2 g full-scale sensor. In the presence of 0.3 g rms vibration (between samples 300 and 600), there is no discernible shift in offset. However, in the presence of 1 g rms vibration (between samples 600 and 1000), the VRE is approximately –100 mg.

 

 

 

The VRE can be modeled as the mean shift of a truncated distribution, limited by the full-scale range of the accelerometer. When the sensor experiences random vibration in a 1 g field, the input excitation can be modeled as a normal distribution with mean µ = 1 g, and standard deviation σ = X, where X denotes the rms input vibration amplitude. The output of the sensor is modeled as a doubly truncated normal distribution, where the output values are bounded by –R and +R, where R is the maximum range of the sensor. The mean of this doubly truncated normal distribution is given as:

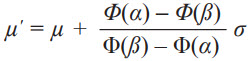
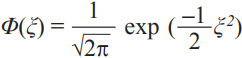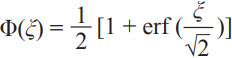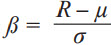Where  is the probability density function and  is its cumulative distribution function. α and β  are defined as  and . The VRE is then obtained as:

Scale Factor Nonlinearity

Nonlinearity is the deviation of the accelerometer output from a best fit straight line over the operating range. The deviation is often expressed as a percentage of the full-scale output. The nonlinearity of the accelerometer can contribute to VRE, as detailed below:

A common model to describe the accelerometer nonlinearity is via an n^th order polynomial. The output a_o (LSBs) can be expressed as a function of the input a_i (g) as follows:

Where:

K₀: offset (LSBs)

K₁: scale factor (LSB/g)

K_n: n^th order coefficient of nonlinearity, n = 2,3, … (LSB/gⁿ)

Consider the case of a simple sinusoidal input acceleration:

The time-averaged value of this input is zero. The output of the accelerometer is then expressed as:

The time-averaged output is equal to the sum of the time-averaged values of all components on the right hand side of the above equation. The odd-order terms average out to zero. Substituting the time averaged values of the even-order terms,

 and   the time-averaged value of the output is given as:

where G_rms is the rms value of the input acceleration. The equation above shows that the second-order nonlinearity translates to a shift in dc offset = (K₂G_rms²) in presence of a sinusoidal vibration. The term  represents the vibration rectification coefficient (VRC) and is specified in units of µg/g²-rms.

Amplitude and Frequency Dependence of Vibration Rectification

For small vibration amplitude, the VRE is dominated by sensor nonlinearity, and it can be expressed in terms of the VRC: VRE = VRC × vib²_rms. However, when the vibration amplitude is larger than the full-scale range, the VRE tends to be dominated by asymmetric clipping as described in the previous section. Also as previously mentioned, any nonzero offset in the accelerometer output also contributes to asymmetric clipping. Most MEMS accelerometers designed for industrial applications have built-in fail-safe circuitry to protect the sensing element from damage in the presence of large vibrations by shutting down the sensor biasing circuit. At large vibration amplitudes, this feature could potentially result in further anomalous shift in offset, thereby worsening the VRE.

Due to the various resonances and filters in the device, VRE often has a strong frequency dependence. The MEMS sensor resonances will amplify vibrations at the sensor’s resonant frequency by a factor equal to the quality factor of the resonance, and damp vibration at higher frequencies, on account of the resonator’s 2-pole response. A sensor with higher quality factor resonance will show greater VRE due to larger amplification of vibrations. Larger measurement bandwidth also leads to higher VRE due to the integration of high frequency in-band vibrations. The analog and digital filters implemented in the signal processing circuitry can suppress the out-of-band vibration peaks and harmonics at the output, but do not have a significant effect on the VRE, as the vibration input is rectified by even order nonlinearity to dc.

Measuring Vibration Rectification

VRE cannot be compensated in real time once an accelerometer has been deployed in the field. In applications where small dc shifts in offset due to vibrations are tolerable, the VRE can be measured to estimate the error in the accelerometer output to determine whether the VRE is within acceptable limits. In any vibration measurement, it is important that the shaker table and test fixture be level, and a precision shaker table must be used to suppress errors arising from shaker cross-axis vibration, offset, and structural resonances. Separately, the test fixture must be designed to the appropriate stiffness to ensure that the fixture resonance frequencies lie well outside the accelerometer bandwidth and the vibration profile band. An optimal fixture design should have its lowest resonance frequency approximately 50% higher than the highest vibration frequency.

Sinusoidal Vibration Profile

The sinusoidal vibration method is most commonly used and described in existing literature, and is covered in IEEE Standard 1293-1998. The general procedure is to apply a sinusoidal vibration input to the accelerometer, and measure the offset shift vs. rms vibration amplitude (vib_rms). The VRC can be estimated from a least squares fit to this data:

This method yields an accurate measurement of the VRC, since the amplitude is well controlled and we can ensure that the accelerometer output does not clip. This test is also useful to identify and quantify the effect of device resonances on the VRE. However, only one frequency can be tested at a time and to adequately capture the sensor performance, this method requires separately testing several frequencies over the accelerometer bandwidth.

Random Vibration Profile

VRE can also be measured using a random vibration input. Typical real-world vibrations are not periodic or predictable like sinusoidal vibration profiles, and hence this method captures the accelerometer’s performance in most applications. By quantifying the shift in offset for broadband excitation in a wide range of frequencies, this method is more useful for simultaneously including all the forcing frequencies and exciting all device resonances. However, the peak-to-peak vibration amplitude is not guaranteed and the VRE thus obtained is an average value over the frequency range.

Figure 2 compares the truncated mean model to measured VRE in the Z-axis sensor of the ADXL355 configured to ±2 g range. In the measurement, the Z-axis is aligned to gravity (1 g field) and a random vibration profile (frequency band 50 Hz to 2 kHz) is applied using an Unholtz-Dickie shaker. The vibration amplitude is measured with a reference accelerometer (PCB Piezotronics model 352C23) and the offset shift is measured while the vibration amplitude is increased beyond the full-scale range. The truncated-mean models (fit to 2.5 g truncation) show a good fit to the measurements. The deviation in the truncation from the programmed full-scale range is expected due to mechanical sensor overhead and output bandwidth constraints (the accelerometer bandwidth in the measured data is 1 kHz, whereas the model does not take the bandwidth into account). The overrange protection circuitry in the ±2 g range is activated when the vibration level reaches 8 g. Gaussian distributed vibration has a crest factor of ≈3, and hence the measured performance starts deviating significantly from the model beyond 2.5 g rms.

 

 

 

Other Factors that Contribute to VRE

The MEMS sensor resonance influences the vibration rectification in the accelerometer. A high quality factor will lead to amplification of vibration signals at frequencies near the sensor resonance, causing larger VRE. This is noticed in the comparison of the VRE performance for the X-axis and Y-axis sensors to the Z-axis sensor in the ADXL355 (±8 g range, 1 kHz bandwidth), which shows peaking of the VRE around 3 g rms in Figure 3, on account of higher Q as compared to the Z-axis sensor.

 

 

 

Using larger than necessary bandwidth for the accelerometer also leads to averaging of higher frequency components, adversely affecting the VRE. This is evident in Figure 4, which shows a comparison of the VRE for a Y-axis sensor in an ADXL355 DUT (±2 g range) for two separate bandwidth settings. The VRE is significantly lower in the 125 Hz bandwidth setting as compared to 1 kHz bandwidth setting.

 

 

 

Conclusion

Many vibration related issues can be avoided by choosing an appropriate bandwidth for the accelerometer to reject high frequency vibrations. Assembly considerations such as package and mounting resonances also influence the VRE by amplifying the vibration coupling at resonance. Ensuring stiff packaging is key to realizing good vibration rectification performance, by setting the package and mounting resonances outside the bandwidth of the accelerometer.

In conclusion, the vibration rectification error (VRE) is an important specification for MEMS accelerometers, and the main sources of VRE and techniques for corresponding measurements are discussed herein. This effect should be kept in mind when designing-in MEMS accelerometers for dc measurements in environments of high vibration. The ADXL355 offers superior vibration rectification, long term repeatability, and low noise performance in a small form factor.