Using the MAXQ3120 in Codec Applications
Abstract
The audio codec is the cornerstone of modern digital telephony. It is the component that converts audible speech into digital data and back to audible speech again. In this article, the A/D channels of the MAXQ3120 and an external DAC are used to encode and decode speech in standard µ-law and A-law format. This leaves a significant amount of processing horsepower available to perform other telecom-related functions, such as call-progress detection and generation, PCM framing, and silent-channel detection.
Download:
(ZIP, 48K)
Introduction
Modern telephony is digital. Gone are the chattering Strowger switches with hundreds of electrical contacts, the miles of twisted-pair cable resembling so much tie-dyed spaghetti, and the microwave towers that once dotted the countryside. Today, voice traffic is converted to digital form at the earliest possible opportunity and carried on an optical fiber alongside thousands of other voice calls, email messages, and web pages.
Digital telephony has fueled the information age and continues to change the communication landscape with technologies like voice over Internet protocol (VoIP). Yet one fact remains—somewhere along the line, voice must be converted to bits, and then bits back to voice.
This is the job of the codec. The word is a contraction of coder/decoder, and the device is conceptually simple. It consists of an analog-to-digital converter (ADC) to change input audio into a stream of bits, a digital-to-analog converter (DAC) to convert the received bitstream into audio, and an interface to insert and remove the digitized audio to and from a bus on which other codecs may be attached.
Typically, a codec is a stand-alone, mixed-signal semiconductor. This is fine as long as the codec is used in a simple application such as a line card for an end-office switch. Often, however, it is desirable to perform some kind of preprocessing of transmitted audio (such as peak limiting, dynamic range compression, or spectral shaping) or post-processing of received audio (such as noise reduction). This is a problem for a stand-alone codec, because once the analog audio is presented to (or taken from) the codec, there is no further opportunity to perform processing—the codec interfaces directly with the PCM highway. In these cases, a system designer is left with two unwieldy options: either perform this processing in the analog domain (often expensive and possibly noisy), or abandon the use of stand-alone monolithic codecs and perform the processing in the digital domain with stand-alone precision ADC and DAC chips. Neither option is ideal. In this article, a method is presented for using the MAXQ3120 with an external DAC as a voice codec that has the ability to perform additional processing of the inbound and outbound bit streams.
Codec Basics
Long before digital telephony was considered, it had been determined that a range of frequencies from about 300Hz to about 3.5kHz must be maintained for a voice signal to remain intelligible. Frequencies outside this range contributed to the fidelity of the speech signal, but not to the intelligibility. (In fact, it turned out that band-limited signals were more intelligible than wideband signals.) Following Nyquist's criterion that a signal must be sampled at least twice as often as the highest frequency of interest, all voice codecs operate at 8,000 samples per second—more than twice the 3.5kHz required—and each sample is converted into a digital codeword.
The size of the codeword, however, presented a problem. In any digital system, there is a tradeoff between signal integrity and word size. For best fidelity, a system designer could choose a large word size, but more bits require greater bandwidth, and bandwidth costs money. Alternately, a designer could select a smaller word size to save bandwidth costs, but voice quality would suffer. Tests indicated that small codewords—about eight bits—would provide good voice quality, but only as long as the speaker spoke in a quiet, consistent voice. Normal variations in voice volume would saturate the transmitter, causing clipping and distortion. One could reduce the gain to eliminate this clipping at high levels, but normal voice levels would use only four or five bits, making soft voices sound scratchy and unnatural. To accommodate the full range of human voices, from the softest whisper to the loudest shout, it seemed that twelve to fourteen bits of resolution would be required.
The solution was to use a nonlinear codec (see Figure 1). These codecs take advantage of the fact that the ear is more forgiving to small errors in loud sounds than it is to small errors in soft sounds. In the figure, silence centers around the zero line; soft voices deviate only a small amount from the center line, and louder voices deviate more greatly. In these devices, codes around the zero line are packed more densely than codes far from the zero line, resulting in a codec that gives acceptable results for low-level signals, while maintaining good dynamic range for high-level signals.
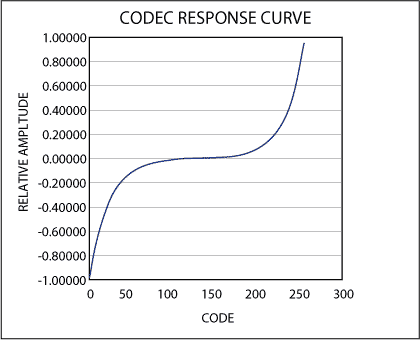
Figure 1. This is the response curve for a typical PCM codec. The region around zero relative amplitude contains many more codes than the ends of the curve, allowing the codec to maintain both high voice fidelity and wide dynamic range.
On the digital side, it is necessary to interface to a PCM highway. Rather than connecting each codec to its associated trunk equipment with a separate set of wires, it is common to connect a number of codecs together on a common bus—a PCM highway. To coordinate transmission, the codecs share a common bit clock and are signaled to begin transmitting or receiving by an individual frame pulse. In a common North American standard, twenty-four codecs can reside on a PCM highway that is clocked at 1,544,000 bits per second by some type of sequencer logic. Every 125µs, the first codec receives a frame pulse and transmits eight bits onto the highway. After eight bit clocks, the second codec receives its frame pulse, and so forth. After all twenty-four codecs have transmitted their data, the sequencer provides one bit time for signaling purposes, and then repeats the sequence. Thus, the numbers are generated as follows:
[(8 bits per sample x 24 channels) + 1 signaling bit] x 8,000 samples per second = 1,544,000 bits
per second
Types of PCM Codecs
The world has standardized on a frame rate (and thus, a sampling rate) for PCM codecs used in telephony. Sadly, the world has standardized on little else. There are two types of transcoding algorithms to consider: A-law, used in Europe, and µ-law, used primarily in the United States and Japan. And there are two basic line rates in use: DS1 (1.544Mb/s) in the United States, and E1 (2.048Mb/s) in Europe. The design presented in this paper is a DS1 (also known as T1) codec, capable of operating in A-law or µ-law mode.
A µ-law codec encodes samples according to the following formula:

where µ is the characteristic of the equation, typically 255.
An A-law codec encodes according to a somewhat different formula:

where A is the characteristic of the equation, usually 87.6; or in some cases, 87.7. Note that for values close to zero, the A-law function is linear; it becomes logarithmic only for input values greater than 1/A.
In actual practice, these two companding laws produce very similar-looking curves. Also, in practice, these linear formulas are virtually never used. Instead, piecewise-linear approximations are called upon to ease computational overhead. The design presented here, however, implements these exact formulas by means of a lookup table.
A Microcontroller Becomes a Codec
The MAXQ3120 contains two precision 16-bit ADC channels and a 16 x 16 multiplier with a 40-bit accumulator. While there is no DAC channel, there are precision serial DACs available at low cost that can serve in this capacity. All that remains is to build software to connect these peripheral devices.
Encoding
There are three steps to encoding: converting the analog signal to digital, resampling and filtering the digitized samples, and finally compressing the samples to an eight-bit representation using either A-law or µ-law transcoding.
First is the A/D conversion step, which is also the easiest because of the ADC channels built into the MAXQ3120. The MAXQ3120 produces a new 16-bit result every 48µs. This means that the system has 384 instruction cycles at a processor clock of 8MHz to process the sample.
Fortunately, processing the sample is a simple matter of reading the ADC and storing the data in a circular buffer. The buffer always contains the 32 most recent 16-bit samples. The MAXQ3120 contains 256 16-bit words of RAM; consequently, the circular buffer consumes only 12.5% of the available RAM for a single channel.
Although the ADC produces a sample every 48µs, the communication networks require a new sample every 125µs. Thus, whatever else we do with the signal, it must be resampled. One trivial method would be to accept only the most recent sample for conversion when a frame pulse is received and to cast away all other samples, but the MAXQ3120 can do better than this.
Upon each frame pulse, the codec software begins applying a 31-tap FIR filter to the accumulated samples in the circular buffer. The filter has a 3db point at 3.5kHz, and thus provides the antialiasing and additional reconstruction that reduces noise in the 
 ADC channels. The result of the filter process is a 16-bit sample ready for A-law or µ-law compression.
ADC channels. The result of the filter process is a 16-bit sample ready for A-law or µ-law compression.
Table 1. First Ten µ-law and A-law Codes
| Code | µ-Law | A-Law |
| 0 | 0000 | 0000 |
| 1 | 0005 | 000F |
| 2 | 000B | 001F |
| 3 | 0011 | 002F |
| 4 | 0018 | 003F |
| 5 | 001F | 004F |
| 6 | 0026 | 005F |
| 7 | 002D | 006F |
| 8 | 0035 | 007F |
| 9 | 003D | 008F |
There are several ways to convert a value from 16-bit linear to its code; direct calculation and piecewise approximation are two popular methods. Rather than use either of these methods, we take advantage of the relatively large program space of the MAXQ3120 by setting up two 128-word tables, one for µ-law encoding and decoding and a second for A-law. At startup, an external pin is polled and, based on the level of that pin, one or the other of the tables is loaded into RAM. The encoding process operates as follows:
- Take the absolute value of the 16-bit linear PCM sample. Keep track of the sign bit.
- Now perform a binary search of the applicable table: compare the PCM sample to the middle value of the table. If less than the middle value, consider only the bottom half of the table; if greater than the middle value, consider only the top half. Repeat until there are only two table entries left, and take the closest one.
- The code to emit is the index of the table entry. For example, if the sample value was 0x006D and the conversion was to A-law, the nearest value in the table above would be 0x006F. Its index is 7; this is the code to emit.
- Finally, apply the sign of the original sample value. The resulting eight-bit number is the logarithmic PCM value. This is not, however, the end. PCM values emitted on the network are not just two's complement binary values. Instead, each transcoding law has special rules that apply.
- Negative numbers have have a zero sign bit; positive values have a one sign bit.
- The magnitude value is inverted: therefore, zero is represented by 0b11111111, while +1 is represented by 0b11111110. This guarantees a large number of one bits in the transmitted stream (many types of physical layer transmission mechanisms have level transitions only on one bits; a high number of one bits thus makes clock recovery easier.)
- There is a "positive zero" value and a "negative zero" value, represented by 0b11111111 and 0b01111111, respectively.
- The largest negative number is -127, represented by 0b00000000. However, to preserve timing integrity, many systems do not permit an all-zero value, These systems automatically prevent the all-zero code by inverting bit 1. This makes in irreversible change to the code stream (0b00000000 becomes 0b00000010) but for audio transmission, it doesn't make much change in the perceived sound—both codes are terribly loud! (This design does not perform this function, but it's an easy change to make.)
- Just as in µ-law, negative numbers have a zero sign bit.
- Just as in µ-law, there is a "negative zero" value and a "positive zero" value, represented by 0b00000000 and 0b10000000, respectively.
- Before transmission, every A-law word is XOR'ed with 0x55; effectively inverting every other bit in the byte. Like inversion for µ-law, this guarantees a high ones density, making clock recovery easier.
Decoding
Decoding an eight-bit PCM sample is much easier than encoding, as no resampling of the signal must be done. Once the PCM law rules have been applied, an eight-bit, signed-magnitude value remains. Use that value as an index into the applicable PCM table (taking sign into account); the result is a 16-bit, signed value ready for delivery to the DAC.
The converter chosen for this project is the MAX5722 dual-channel DAC. This is a 12-bit DAC in an economical eight-pin µMAX package. Like most DACs, the MAX5722 requires an external voltage reference. Fortunately, there is a 1.25V bandgap voltage reference on the MAXQ3120 suitable for this purpose.
The MAX5722 is a serial interface DAC, meaning the microcontroller must create a serial stream suitable for the DAC. The DAC interface is synchronous, so it doesn't need a continuous clock—it only requires a clock when chip select is low. This allows the use of a three-wire interface using only general-purpose I/Os from the microcontroller.
Note that, in this design, the input range for the ADC channels is -1.0V to +1.0V, while the range for the DAC output channels is 0.0V to +1.25V. In a real telecommunications application, such as a line card, it is likely that these levels would be translated to some other analog level (it is common, for example, to define 1mW into a 600Ω impedance as 0dBm, the maximum level typically encountered in a telecommunications network). If keeping the input and output levels identical is important in your application, see the MAX5722 data sheet for details on producing a bipolar output.
The PCM Bus
Now that we know how to convert analog waveforms into compressed PCM format and back, only one issue is left: interfacing with the PCM bus.
Most often, interfacing with a PCM highway involves connecting to a four-wire bus: a transmit data line upon which terminals place their data; a receive data line upon which the trunk equipment places its data and from which the terminals receive data; a frame sync line that typically is unique to each terminal that pulses to indicate when the bus contains data intended for that terminal; and a bit clock. Since our codec is intended as terminal equipment, it will receive the bit clock and the frame pulse, receive data on the receive data line, and transmit its data on the transmit data line.
In a T1 system, the clock runs at 1.544MHz. That means we must respond very quickly, within only a few clock cycles, when a frame pulse arrives. One bit time is a little more than 625ns, or five instruction cycles. Since this time is much less than typical interrupt latency (when the interrupt, context save and overhead are considered), simply responding to the frame pulse signal with an interrupt is not fast enough—another solution must be found.
That solution is to use one of the three timers in the MAXQ3120 to interrupt the processor a few microseconds before the frame pulse is expected to arrive. Then, when the frame pulse finally arrives, the processor has been interrupted, has saved its context, and is ready to dedicate every cycle to the PCM bus task. It works as follows: Set up a timer to expire in 110µs. Start the timer at the end of each frame event after all bits have been shifted out. In a T1 system, two samples are shifted out in 10.4µs. When the timer interrupts the processor, software immediately begins looking for the leading edge of a frame pulse. This is the only interrupt in the system. Everything else is polled and can wait until the important task of getting the PCM data on and off the bus is completed.
Once the frame pulse arrives, the processor stays very busy. It has to shift the transmit buffer and write the output bit to the port, and then read the input bit and shift the receive buffer in five cycles. The MAXQ3120 does this in exactly five cycles.
You may notice that this discussion has centered around a T1 bus, but what about E1? At 2.048MHz, the E1 system only allows a little more than 488ns—or less than four instruction cycles—per bit. Thus, management of an E1 PCM bus would require help from external hardware. For example, an inexpensive shift register driven from the bit clock would provide relief from the rigors of bit-level timing.
Additional Features
The codec is complete. However, as stand-alone codecs are inexpensive and plentiful, it makes no sense to build a codec out of a microcontroller unless, of course, as a designer, you have an ulterior motive. Here are a few ideas that might motivate a designer to consider such a system:
- Prefiltering While the signal is in the linear PCM format, it is a perfect opportunity to apply equalization, dynamic range compression, noise gating, or any number of other operations on the signal. Although the MAXQ3120 is not a DSP in the traditional sense, these functions are easily within the range of horsepower available in the processor.
- In-Band Signaling Extraction Efficient, simple algorithms are available to detect in-band tones in a linear PCM stream. These algorithms could be exploited to detect DTMF digits and use those to enable certain features and functions. One could also use tone detection to determine the progress of a call by precisely detecting dial tone (in North America, 350Hz + 440Hz), station ring (440Hz + 480Hz), and busy signal (480Hz + 620Hz).
- Conference Bridge It is simple to mix the received audio of channel 1 and combine it with the transmitted audio of channel 2, and vice versa. By doing this you have effectively created a digital conference bridge for two channels. Since the bridge is digital, there is no loss of voice quality. If you wish to bridge more than two channels, simply add more MAXQ3120 devices.
Conclusion
While the MAXQ3120 is not specifically targeted to the telecommunications community, its on-chip precision ADCs and DSP functionality provide the designer with a broad range of opportunities to create customized hardware and software solutions. The availability of a wide range of development tools makes the design task simple.
About the Authors
Related to this Article
Products
12V, Ultra-Low-IQ, Low-Dropout Linear Regulators with POK
12-Bit, Low-Power, Dual, Voltage-Output DAC with Serial Interface




















