Abstract
Reducing electromagnetic interference (EMI) has become an important design issue for electronic system designers. A spread-spectrum clock (CLK) is an efficient way to reduce EMI. This article describes how the spread-spectrum CLK is defined, and provides a simple formula for estimating the EMI suppression. The resulting formula is verified by data generated by the Maxim CLK Generation chip, MAX9492.
There are two major forms of digital signals: digital-data and digital-clock (CLK).
Digital signals are the principal signal form in today's digital electronic products. They are usually generated as a single-ended signaling format, such as CMOS or TTL. A digital-data signal can be viewed as a sequence of pulses with different pulse widths; a CLK signal is usually a string of rectangular pulses with the same pulse width.
The frequency components of both the digital-data signal and CLK signal contain high-order harmonics. Together, the signal itself and the harmonics create electromagnetic interference (EMI) in and between electronic systems. A simple and efficient way to reduce EMI is to implement a dither on the CLK frequency [1, 2]. This application note introduces a spread-spectrum CLK, the MAX9492, and provides a quick calculation of EMI reduction using the parameters specified for the CLK.
Spread-Spectrum CLK: Definition and Measurement
Creating a spread-spectrum CLK by dithering the CLK frequency is not as straightforward as it might appear. We begin by defining parameters that comprise a spread-spectrum CLK: spreading rate, spreading style, modulation rate, and modulation waveform. Spreading rate is the ratio of the range of dithering (or spreading) frequency over the original CLK frequency, fC. Spreading style is down-spreading, center-spreading, or up-spreading. If we assume that the spreading frequency range is Δf, the spreading rate, δ, is defined as:
Down spreading: δ = -Δf /fC x 100%
Center spreading: δ = ±1/2Δf/fC x 100%
Up spreading: δ = Δf/fC x 100%
Modulation rate, fm, is used to determine the CLK-frequency spreading-cycling rate, and is the time during which the CLK frequency varies through Δf and returns to the original frequency. The modulation waveform describes the CLK frequency variation curve in terms of time, often represented by a sawtooth waveform. Figure 1 shows the modulation waveform and its relation to δ and fm.

Figure 1. Frequency profile of spread-spectrum CLK.
To make the CLK spectrum flatter, a special curve, named a "Hershey Kiss™," is used as the modulation waveform (Figure 2).
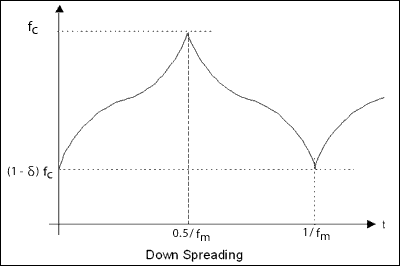
Figure 2. 'Hershey Kiss' modulation waveform.
A CLK spread by the waveforms shown in Figures 1 or 2 has a flat power density in the spreading range. Figure 3 shows the curves of the CLK spectrum of MAX9492 with and without frequency spreading. In this case, the spreading rate, δ, is -2.5 down-spreading. The modulation rate, fm, is 30kHz, and the CLK normal frequency, fC, is 133.33MHz. This spectrum plots are measured by a Rohde & Schwarz spectrum analyzer with a 100kHz resolution bandwidth and a 10Hz sweeping rate. As the plots show, the spectrum peak is reduced by about 13dB and similar attenuation happens at the harmonics of fC. This indicates that this spread-spectrum CLK provides a 13dB EMI reduction on the spectrum peak.

Figure 3. A CLK spectrum of the MAX9492 with and without spreading.
A Quick Estimation of EMI Reduction Level
Designers often ask how EMI suppression relates to the parameters of a spread-spectrum CLK. To examine that relationship, we first calculate the spectrum of a spreading CLK. From the definition above, signal spectrum is the power density with respect to frequency. To make the analysis simple, we only consider the fundamental harmonic of a CLK signal. For a nonspreading CLK, it can be represented as
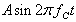
and for a spreading CLK as

where  is the modulation waveform. The spectrum of the nonspreading CLK is a spectral line at frequency fC with the amplitude of
is the modulation waveform. The spectrum of the nonspreading CLK is a spectral line at frequency fC with the amplitude of

As this spectrum is a spectral line, its amplitude is not dependent on the resolution bandwidth B of the spectrum analyzer. However, the spectrum amplitude of a spreading CLK is dependent on the resolution bandwidth B. Since the spreading CLK's power spreads fairly evenly in a frequency band with a range of Δf, the approximate power measured in the resolution band B of the spectrum analyzer is

We can, therefore, express the EMI reduction rate, S, as:
EMI Suppression Rate (dB) 
Referring back to the spread-spectrum CLK parameters of spreading rate δ, CLK frequency fC, and modulation styles, we calculate S in the following way:
Down or up spreading: 
Center spreading: 
One should notice that the EMI suppression rate, S, is unrelated to modulation rate fm as long as fSW << fm << fC, where fSW is the sweeping rate of spectrum analyzer.
As an example, the values of δ and fC of the MAX9492 are -2.5% and 133.3MHz, respectively. Substituting these values into Equation (2a), you can calculate the EMI reduction rate as:

As measured in Figure 3, the EMI peak reduction is 12.91dB and the EMI reduction to the average level of the spread spectrum is 15.07dB. Generally, when estimating the EMI reduction between the peaks, the estimate obtained from Equation 2 could be over by 1dB to2dB due to the ripple of spread spectrum. For the reduction between the peak and the average level, however, the estimate is very close to the measured reduction.
With this simple estimate of the EMI reduction, a designer can quickly determine the spreading rate for the desired EMI reduction rate, the CLK frequency, and the spectrum resolution bandwidth required by the electromagnetic compatibility regulations.




















