Overview
Design Resources
Design & Integration File
- Schematic
- Bill of Materials
- Gerber Files
- PADS Files
- Assembly Drawing
Evaluation Hardware
Part Numbers with "Z" indicate RoHS Compliance. Boards checked are needed to evaluate this circuit.
- EVAL-CFTL-6V-PWRZ ($23.01) Wall Power Supply for Eval Board
- EVAL-CN0189-SDPZ ($81.21) Tilt Measurement Using a Dual Axis Accelerometer
- EVAL-SDP-CB1Z ($134.00) Eval Control Board
Device Drivers
Software such as C code and/or FPGA code, used to communicate with component's digital interface.
Features & Benefits
- 1 Degree Accuracy over 90 Degrees and Temperature
- Dual axis to ensure precise accuracy
- Filtered to reduce inband noise
- Precision tilt applications
Product Categories
Markets and Technologies
Parts Used
Documentation & Resources
-
CN0189 Software User Guide10/18/2018WIKI
-
MT-101: Decoupling Techniques2/14/2015PDF954 kB
-
MT-031: Grounding Data Converters and Solving the Mystery of "AGND" and "DGND"3/20/2009PDF144 kB
-
CN-0189: Tilt Measurement Using a Dual Axis Accelerometer4/11/2012PDF285 kB
Circuit Function & Benefits
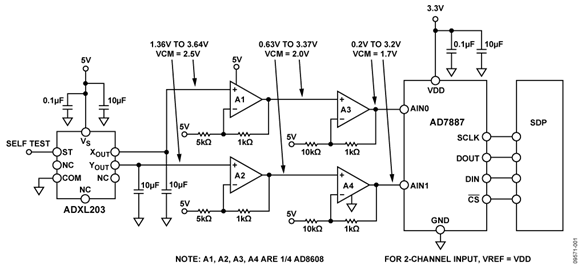
The circuit, shown in Figure 1, incorporates a dual axis ADXL203 accelerometer and the AD7887 12-bit successive approximation (SAR) ADC to create a dual axis tilt measurement system.
The ADXL203 is a polysilicon surface micromachined sensor and signal conditioning circuit. Acceleration in the X or Y axis will produce a corresponding output voltage on the XOUT or YOUT output pins of the device. The X axis and Y axis are perpendicular to one another. The AD8608 quad op amp buffers, attenuates, and level shifts the ADXL203 outputs so they are at the proper levels to drive the inputs of the AD7887. The rail-to-rail input/output AD8608 is chosen for its low offset voltage (65 μV maximum), low bias current (1 pA maximum), low noise (8 nV/√Hz), and small footprint (14-lead SOIC or TSSOP).
The AD7887 is configurable for either dual or single channel operation via the on-chip control register. In this application it is configured for dual channel mode, allowing the user to monitor both outputs of the ADXL203, thereby providing a more accurate and complete solution.
The system maintains an accuracy of 1° over 90° and over temperature. The circuit provides this precision, performance, and range in a low cost, low power, small footprint, calibration dependent solution. The ADXL203 is specified over a minimum temperature range of −40°C to +105°C and is available in an 8-terminal ceramic leadless chip carrier package (LCC).

Circuit Description
Supply Voltage and Decoupling
The ADXL203 requires only one 0.1 μF decoupling capacitor as long as there is no noise present at the 140 kHz internal clock frequency. If necessary, larger bulk capacitors (1 μF to 10 μF) or ferrite beads can be included.
In order to have output logic levels compatible with the SDP board, the AD7887 must run on a +3.3 V rail. The rest of the circuit, as indicated in Figure 1, uses the +5 V rail. The ADXL203 is specified and tested with a nominal supply voltage of +5 V. Although the ADXL203 is operational with a supply voltage anywhere between 3 V and 6 V, optimum overall performance is achieved at 5 V. Please refer to the ADXL203 data sheet for details regarding performance at other supply voltages.
The ADXL203 outputs are ratiometric; increasing the supply voltage will act to increase the output voltage. The output sensitivity varies proportionally to supply voltage. At VS = 3 V, the output sensitivity is typically 560 mV/g. At Vs = 5 V, the device has a nominal sensitivity of 1000 mV/g.
The zero-g output level is also ratiometric, so the zero-g output is nominally equal to VS/2 at all supply voltages.
The output noise of the ADXL203, however, is not ratiometric but absolute in volts. This means the noise density will decrease as the supply voltage increases. This is because the scale factor (mV/g) increases while the noise voltage remains the same. For VS = 3 V, the noise density is typically 190 μg/√Hz and 110 μg/√Hz for VS = 5 V.
Noise, Bandwidth, and Output Capacitor Selection
The ADXL203 noise has the characteristics of white Gaussian noise, which contributes equally at all frequencies. It is described in terms of μg/√Hz (the noise is proportional to the square root of the accelerometer bandwidth). The user should limit bandwidth to the lowest frequency needed by the application to maximize the resolution and dynamic range of the accelerometer.
The bandwidth is set by a capacitor (CX,Y) on the XOUT and YOUT pins of the device. These capacitors create a low-pass filter when combined with the internal 32 kΩ output resistor of the ADXL203. These filters are intended primarily for noise reduction and antialiasing. The equation for the 3 dB bandwidth is:
BW = 1/(2πR×C(X,Y)), where R = 32 kΩ
With the single poll roll-off characteristic, the typical noise of the ADXL203 on a 5 V supply is determined by:
RMS Noise = (110 μg/√Hz) × √(BW × 1.57)
Often, the peak-to-peak noise is desired as it gives the best estimate of the uncertainty in a single measurement; peak-topeak noise is estimated by multiplying the rms value by 6.
Table 1 gives the bandwidth, rms noise, and peak-to-peak noise for a given filter capacitor. For this circuit, two 10 μF capacitors create a bandwidth of 0.5 Hz. A minimum capacitance of 2000 pF is required in all cases.
| Bandwidth (Hz) | CxCy (µF) | RMS Noise (mg) | Peak-to-Peak Noise Estimate (mg) |
| 10 | 0.47 | 0.4 | 2.6 |
| 50 | 0.1 | 1.0 | 6 |
| 100 | 0.047 | 1.4 | 8.4 |
| 500 | 0.01 | 3.1 | 18.7 |
Physical Operation of Sensor
The sensor is a surface micromachined polysilicon structure built on top of the silicon wafer. Polysilicon springs suspend the structure over the surface of the wafer and provide a resistance against acceleration forces. Deflection of the structure is measured using a differential capacitor that consists of independent fixed plates and plates attached to the moving mass.
The fixed plates are driven by 180° out-of-phase square waves. Acceleration deflects the beam and unbalances the differential capacitor, resulting in an output square wave whose amplitude is proportional to acceleration. Phase-sensitive demodulation techniques are then used to rectify the signal and determine the direction of the acceleration.
Input Vector and Part Orientation
The input signal to the ADXL203 is not a standard current or voltage. Instead, the accelerometer uses the force of gravity as an input vector to determine the orientation of an object in space. Figure 2 shows the ADXL203 in five different orientations with respect to the earth’s surface and the corresponding output voltages based on the orientation of the sensor.
When the axis of interest (the X-axis for this example) is oriented parallel to the Earth’s surface, the sensor experiences a 0 g field, which corresponds to a zero-g bias level of 2.5 V. The output voltage will change according to the sensitivity of the device (1000 mV/g). Therefore, rotating 90° clockwise (counterclockwise) will produce a +1 g field (−1 g field) and corresponding output voltage of 3.5 V (1.5 V). For various IC orientations and their associated output voltages, see Figure 2.

Conditioning the ADXL203 Voltage Output
In order to process the accelerometer data and calculate an angle, the information must be digitized by the AD7887. It is necessary to determine the ADXL203 worst-case output voltage range and compare it to the ADC input voltage range. The AD7887 has an input voltage range of (0 V to VDD = 3.3 V). The ideal ADXL203 output voltage range is (1.5 V to 3.5 V). However, several non-idealities have been neglected in determining this range.
The first non-ideal characteristic is the zero-g bias level. This voltage is specified for 2.4 V to 2.6 V, a worst-case shift of 100 mV up or down. The second non-ideal characteristic is the sensitivity of a particular output, with a worst-case specification of 960 mV/g to 1040 mV/g. By combining both of these errors, the ADXL203 worst-case output range can be calculated:
VMAX (+1 g) = (2.6 V) + (1040 mV/g)×(+1 g) = 3.64 V
VMIN (−1 g) = (2.4 V) + (1040 mV/g)×(−1 g) = 1.36 V
Now that the accelerometer output range has been determined, the objective is to manipulate this range (1.36 V to 3.64 V with VCM = 2.5 V) to fit the ADC input range. For dual channel operation, the AD7887 input range is 0 V to VDD (0 V to 3.3 V with VCM = 1.7 V). The quad AD8608 is used to create a 2-stage conditioning circuit as seen in Figure 1.
The first stage provides a signal gain of 1.2 and level shifts the common-mode voltage to 2 V. The second stage provides a signal gain of 1.1 (for a total signal gain of 1.32) and establishes the common-mode output voltage of 1.7 V. The output voltage range of this op amp stage lines up nicely with the ADC input voltage range, leaving approximately 200 mV headroom on the negative end and 100 mV on the positive end.
Single Axis Tilt Calculation
As an example, consider a single axis solution as indicated in Figure 3. Referring to trigonometry, the projection of the gravity vector on the X axis produces output acceleration equal to the sine of the angle between the accelerometer X axis and the horizon. The horizon is typically taken to be the plane orthogonal to the gravity vector. For an ideal value of 1 g for gravity, the output acceleration is:
AX, OUT [g] = 1 g × sinθ
Conversion from acceleration to an inclination angle is done using the inverse sine function.
θ = sin-1 (AX, OUT [g]/ g)
where the inclination angle, θ, is in radians.

It is important to note when using a single axis solution, the sensitivity decreases as the angle between the horizon and the X axis increases. The sensitivity approaches zero as the angle approaches ±90°. This can be seen in Figure 4, where the output acceleration in g is plotted against the angle of inclination. Near ±90°, a large change in inclination angle results in a small change in output acceleration.
It is important to be cautious of signals that are out of range. It is possible for the accelerometer to output signals greater than ±1 g due to vibration, shock, or other sudden accelerations.

Single Axis vs. Dual Axis Considerations
A simple way of addressing the decreasing sensitivity of a single axis solution as it rotates through 90° is to include a second axis perpendicular to the original. There are three major benefits to including a second axis in determining the angle of inclination.

The second major benefit of using at least two axes is that unlike the single axis solution, where tilt in any other axis will cause significant error, the use of a second axis allows an accurate value to be measured even when inclination in the third axis is present. This is because the sensitivity is proportional to the root-sum-square (rss) value of gravity on the axes of interest.

The third major benefit of using a secondary axis is the ability to distinguish between each quadrant and to measure the angles throughout an entire 360° arc. Each quadrant has a different combination of signs associated with the X and Y axis acceleration.
The inverse tangent function returns a value in Quadrant I if the operand, AX, OUT/ AY, OUT is positive; if the operand is negative, the inverse tangent function returns a value in Quadrant IV. Because the operand in Quadrant II is negative, a value of 180° should be added to the result of the calculation when the angle is in that quadrant. Because the operand in Quadrant III is positive, a value of 180° should be subtracted from the result of the calculation when the angle is in that quadrant. The correct quadrant of the calculated angle can be determined by examining the sign of the measured acceleration on each axis.
Dual Axis Tilt Calculation
Now that a second axis is included in the system, the inclination angle calculation also requires a second look. The simple approach is to calculate the X axis as before, and to calculate the Y axis in a similar fashion, remembering to use the cosine of the angle.
AX, OUT [g] = 1 g × sin θ
AY, OUT [g] = 1 g × cos θ
Convert from acceleration to an angle using the inverse sine and cosine functions.
θ = sin-1 (AX, OUT [g]/ 1 g)
θ = cos-1 (AY, OUT [g]/ 1 g)
where the inclination angle, θ, is in radians.
It is easier, however, to apply a trigonometric identity by using the ratio of the values, which results in the following:

where the inclination angle, θ, is in radians.
Calibration
The most critical design aspect of the accelerometer circuit in Figure 1 is the ability to calibrate the system. Without accurate calibration, proper test procedure, and setup, the system will produce errors much larger than desired. The CN0189 Labview software includes a predefined system calibration procedure. Next, we will discuss not only how to calibrate this system, but also what contributes to the errors and why the calibration is necessary.
Effects of Offset Error
Imagine first a dual axis solution with perfect sensitivity but with a 50 mg offset on the X axis. At 0° the X axis reads 50 mg, and the Y axis reads 1 g. The resulting calculated angle would be 2.9°, resulting in an error of 2.9°. At ±180° the X axis would report 50 mg, whereas the Y axis would report −1 g. This would result in a calculated angle and error of −2.9°.
The error between the calculated angle and the actual angle is show in Figure 7 for this example. The error due to an offset may not only be large compared to the desired accuracy of the system, but it can vary, thus making it difficult to simply calibrate out an error angle. This becomes more complicated when an offset for multiple axes is included.

Effects of Sensitivity Mismatch Error
The main error component in a dual axis inclination sensing application is a difference in sensitivity between the axes of interest (in a single axis solution, any deviation between actual sensitivity and expected sensitivity results in an error). Because the ratio of the X and Y axes is used, most of the error is canceled if the sensitivities are the same.
As an example of accelerometer sensitivity mismatch, assume a dual axis solution with perfect offset trim, perfect sensitivity on the Y axis, and +5% sensitivity on the X axis. In a 1 g field, the Y axis reports 1 g and the X axis reports 1.05 g. Figure 8 shows the error in the calculated angle due to this sensitivity mismatch. Similar to offset error, the error due to accelerometer sensitivity mismatch varies over the entire range of rotation, making it difficult to compensate for the error after calculation of the inclination angle.

No-Turn Calibration Technique
When the errors due to offset and sensitivity mismatch combine, the total error can become quite large and well beyond acceptable limits in inclination sensing applications. To reduce this error, the offset and sensitivity should be calibrated, and the calibrated output acceleration used to calculate the angle of inclination. When including the effects of offset and sensitivity, the accelerometer output is as follows:
AOUT[g] = AOFF + (Gain × AACTUAL)
where:
AOFF is the offset error, in g.
Gain is the gain of the accelerometer, ideally a value of 1.
AACTUAL is the real acceleration acting on the accelerometer and the desired value, in g.
A simple calibration method is to assume the gain is 1 and to measure the offset. This calibration then limits the accuracy of the system to the uncalibrated error in sensitivity. The simple calibration method can be done by placing the axis of interest into a 1 g field and measuring the output, which would be equal to the offset. That value should then be subtracted from the output of the accelerometer before processing the signal. This is often referred to as a no-turn or single point calibration because the typical orientation of a device puts the X and Y axes in a 0 g field. If a 3-axis device is used, at least one turn or a second point should be included for the Z axis.
Multiple Turn Calibration Technique
A more accurate calibration method is to use two points per axis of interest. When an axis is placed into a +1 g and −1 g field, the measured outputs are as follows:
A+1g[g] = AOFF + (1 g × Gain)
A−1g [g] = AOFF + (−1 g × Gain)
where the offset, AOFF, is in 'g’.
These two points are used to determine the offset and gain as follows:
AOFF [g] = 0.5 × (A+1g[g] + A-1g[g])
Gain = [0.5 × (A+1g[g] + A-1g[g])]/ 1 g
where the +1 g and −1 g measurements, A+1g[g] and A-1g[g], are in g.
This type of calibration also helps to minimize cross-axis sensitivity effects as the orthogonal axes are in a 0 g field when making the measurements for the axis of interest. These values are used by first subtracting the offset from the accelerometer measurement and then dividing the result by the gain.
AACTUAL[g] = (AOUT – AOFF) / Gain
The calculations of AOFF and Gain in the above equations assume that the acceleration values, A+1g and A−1g, are in g.
If acceleration in mg is used, the calculation of AOFF remains unchanged, but the calculation of Gain is divided by 1000 to account for the change in units.
Test Results
The PCB was mounted to a board capable of spinning freely through 360°, and a set of data was taken using the calibration technique described above (finding the +1 g and −1 g values for both the X axis and Y axis to determine the offset and sensitivity of each axis). The PCB was oriented so the Y axis outputs a +1 g voltage level (~3.5 V), and the X axis outputs a 0 g voltage level (~2.5 V). This orientation, after calibration, is considered 0°.
The PCB was then rotated through ±90° in 1° increments. Figures 9 and 10 show the errors of the X and Y axis, respectively.



The errors begin to increase on both axes as they approach their respective ±1 g readings. This corresponds to a board orientation of ±90° for the X axis, and 0° for the Y axis.
Figure 11 shows the error according to the arctangent of the X axis and the Y axis. Notice how the error of the ratio of the two axes does not have the boundary restrictions observed in Figure 9 and Figure 10.
PCB Layout Considerations
In any circuit where accuracy is crucial, it is important to consider the power supply and ground return layout on the board. The PCB should isolate the digital and analog sections as much as possible. The PCB for this system was constructed in a 4-layer stack up with large area ground plane layers and power plane polygons. See the MT-031 Tutorial for more discussion on layout and grounding and the MT-101 Tutorial for information on decoupling techniques.
The power supply to the AD7887 should be decoupled with 10 μF and 0.1 μF capacitors to properly suppress noise and reduce ripple. The capacitors should be placed as close to the device as possible with the 0.1 μF capacitor having a low ESR value. Ceramic capacitors are advised for all high frequency decoupling.
Power supply lines should have as large a trace width as possible to provide low impedance paths and reduce glitch effects on the supply line. Clocks and other fast switching digital signals should be shielded from other parts of the board by digital ground.
A complete design support package for this circuit can be found at www.analog.com/CN0189-DesignSupport.
Common Variations
The sensitivity of the ADXL203 and the gain of the AD7887 are both proportional to their respective supply voltages in the circuit. The entire circuit can be made ratiometric by deriving the 3.3 V VDD supply from the 5 V supply using a resistive divider followed by an AD8605 buffer as shown in Figure 12.

This configuration minimizes circuit sensitivity to supply voltage variations. The AD8505 and AD8606 are single and dual versions of the AD8608 and can be used in the circuit if desired.
Circuit Evaluation & Test
This circuit uses the EVAL-CN0189-SDPZ circuit board and the EVAL-SDP-CB1Z System Demonstration Platform (SDP) evaluation board. The two boards have 120-pin mating connectors, allowing for the quick setup and evaluation of the circuit’s performance. The EVAL-CN0189-SDPZ board contains the circuit to be evaluated, as described in this note, and the SDP evaluation board is used with the CN-0189 evaluation software to capture the data from the EVAL-CN0189-SDPZ circuit board.
Equipment Needed
- PC with a USB port and Windows® XP or Windows Vista® (32-bit), or Windows® 7 (32-bit)
- EVAL-CN0189-SDPZ circuit evaluation board
- EVAL-SDP-CB1Z SDP evaluation board
- CN-0189 evaluation software
- Power supply: +6 V, or +6 V “wall wart”
Getting Started
Load the evaluation software by placing the CN0189 Evaluation Software disc in the CD drive of the PC. Using "My Computer," locate the drive that contains the evaluation software disc and open the Readme file. Follow the instructions contained in the Readme file for installing and using the evaluation software.
Functional Block Diagram
See Figure 1 of this circuit note for the circuit block diagram, and the file “EVAL-CN0189-SDPZ-SCH-Rev0.pdf ” for the circuit schematics. This file is contained in the CN0189 Design Support Package.
Setup
Connect the 120-pin connector on the EVAL-CN0189-SDPZ circuit board to the connector marked “CON A” on the EVAL-SDP-CB1Z evaluation (SDP) board. Nylon hardware should be used to firmly secure the two boards, using the holes provided at the ends of the 120-pin connectors. Using an appropriate RF cable, connect the RF signal source to the EVAL-CN0189-SDPZ board via the SMA RF input connector.
With power to the supply off, connect a +6 V power supply to the pins marked “+6 V” and “GND” on the board. If available, a +6 V "wall wart" can be connected to the barrel connector on the board and used in place of the +6 V power supply. Connect the USB cable supplied with the SDP board to the USB port on the PC. Note: Do not connect the USB cable to the mini USB connector on the SDP board at this time.
Test
Apply power to the +6 V supply (or “wall wart”) connected to EVAL-CN0189-SDPZ circuit board. Launch the evaluation software, and connect the USB cable from the PC to the USB mini-connector on the SDP board.
Once USB communications are established, the SDP board can be used to send, receive, and capture serial data from the EVAL-CN0189-SDPZ board.
Information and details regarding test setup, calibration, and how to use the evaluation software for data capture can be found in the CN0189 Evaluation Software Readme file.
Information regarding the SDP board can be found in the SDP User Guide.