Use a Single Input to Acquire Two Similar Signals Simultaneously and Other AC Techniques for the LTC1864
Use a Single Input to Acquire Two Similar Signals Simultaneously and Other AC Techniques for the LTC1864
2002-08-01
If you have the processing power of a digital signal processor available, the LTC1864 ADC has the AC performance necessary to simultaneously digitize two signals in the 60Hz to 50kHz range. This technique allows you to retain the 250kHz sample frequency whereas multiplexing two channels would cut the sampling frequency in two. The technique described here uses the region near Nyquist for a second measurement channel, assuming the use of an FIR filter will suppress this region in the case of the first channel.
In Figure 1 the second channel (f2) is modulated with Nyquist frequency (1/2 • fS) in order to make it appear at Nyquist – f2. The subsequent digital processing of this second channel involves inverting every other sample to invert the entire spectrum, restoring the original frequency of f2, and making f1 appear near Nyquist. The frequency range of the individual channels must roll-off significantly before Nyquist, either by use of a filter, or due to naturally occurring phenomena such as a vibration that tends to roll-off at between 12 and 18 dB per octave.

Figure 1. Second frequency modulated with Nyquist frequency.
The frequencies of interest in the two data paths can be isolated by the use of either identical or specifically tailored FIR filters. The two frequencies in the example are at 5.065kHz, and 4.883kHz; 183Hz apart.
The 250ksps sampling rate allows the use of simple 1st or 2nd order antialiasing filtering to measure lower frequency physical phenomena such as vibration. This, in addition to being less costly than a higher order antialiasing filter, may make it possible to implement a more nearly ideal overall pass band characteristic using a digital FIR to define cut-off rather than a physical filter. A higher sample frequency relative to the band of interest will allow the use of an FIR filter having some combination of lower pass band ripple, sharper roll-off, better phase linearity, less delay or better stop-band rejection. A higher sample frequency allows a longer FIR filter for a given latency, and when the pass band is a small fraction of the Nyquist frequency, nonideal artifacts resulting from the use of an FIR filter with noncoherent frequencies are reduced.
By using a sample frequency significantly greater than the frequency range of interest, it is possible to extend resolution beyond the resolution of the converter. DNL can be reduced using dither, but INL is no better than that of the converter.
For example, an increase in sampling frequency from 44kHz to 220kHz, a factor of 5 increase, results in improvement in signal to noise ratio is proportional to the square root of 5, or 7dB.
If the primary measurement function is related to the DC to 20kHz range, and if the intent is to implement an FIR filter in any case to produce a suppression of higher frequency components, decimation filtering or to provide programmable cut-off frequencies, you may want to consider using the region near Nyquist (fs/2) for a second signal. This second signal could be the result of excitation of a sensor at or near Nyquist, or this signal can fall into the same DC to 20kHz range and be modulated by a mixer at Nyquist.
In the case of the LTC1864, this second signal can be driven into the second (inverting input) as if it were simply a second input (see Figure 1). If a larger number of sensors were required, it may be better to sum as many as 20 or 30 inputs into a single high performance low noise amplifier such as the LTC1468 (see Figure 2)

Figure 2. Using a large number of sensors.
In the first case, the second signal is modulated at Nyquist by using an analog multiplexer alternating between inverted and noninverted signal paths.
The subsequent sample processing involves inverting every other sample, and running this sample stream through possibly the same FIR filter algorithm as is used for the first channel. This action of inverting every other sample in the digital domain converts this signal back to its original frequency region. In this second representation of the input data, the lower frequency content associated with the first channel then appears near Nyquist. The FIR filter can be optimized to maximize suppression in the region approaching Nyquist.
As the samples defining these two signals are taken at exactly the same time, there is no differential delay between the two signals. The samples are effectively simultaneous.
Relative to a true simultaneous sampling converter this approach of using a single channel may save money on the converter and the cost of the serial interface.
An equivalent 2-channel scheme would require 500ksps or an average data transfer of somewhat higher than 8 Mbps.
Why is this better than multiplexing the two signals in a conventional manner? It is better primarily because it leaves Nyquist at 125kHz rather than halving it to 62.5kHz. If the second channel requires lower resolution, the loss of dynamic range on the first sample is minimal, and in fact, the second may act as dither for the first.
If the amplitude of the input signals falls off naturally with frequency, this approach could be used to acquire two signals with relatively flat response to 50kHz as the antialiasing filter then does not require a steep roll-off.
As the two signals will add, the maximum input signal for each is limited to –6dBfs unless they are unequally weighted, or unless the simultaneous occurrence of high-level signals is impossible.
Circuit Description
Figure 1 shows f1 passing through a level-shift bias circuit that raises the nominal input voltage at pin 2 to 3.25V to optimize the input range for AC, assuming that the inverting input (pin 3) is at a nominal bias voltage of 0.5V. R1 would be 6.04K, and R2 would be 3.32K for this example. If this input is to be used for DC in the 1V–5V range, these resistors are not necessary. The biasing of the LT1806 produces a nominal output voltage of 0.5V.
These values are assuming the maximum signal at f1 is –3dBfs, and f2 is –15dBfs. If –15dB seems low, narrow band filtering performed on f2 can produce good SNR.
In other examples of reuse of frequency spectrum, Nyquist frequency can be used to excite sensors from thermistors to capacitive proximity sensors, or inductive sensors. The use of AC can be used to sense across a large potential difference, for example, chopping a small current sense voltage sitting at 150V, and AC coupling the resulting signal using a capacitor rather than using an expensive isolated subsystem. Yet another example may involve optical excitation at Nyquist.
In another example (Figure 2), a large number of capacitive proximity sensors can be summed, but the total signal must not exceed full scale. In the case where 32 channels are summed, the maximum signal level on any channel must be –30dBfs unless the simultaneous occurrence of all signals is prevented.
This use of a large number of channels using AC frequency components can be isolated from each other using either an FFT, or a series of Discrete Fourier Transforms (DFT) tailored to each frequency. The advantage of the DFT is that less memory is required, and it can be done as the samples are acquired, as opposed to the very orthogonal FFT that requires that all samples be available before the algorithm is begun. The DFT however quickly becomes impractical beyond isolating a few frequencies.
In these cases where many excitation frequencies are used1 and distinguished by transforming into the frequency domain, the frequencies should be “coherent” with the sample window. This means that there are an exact integral number of sinusoids of each frequency in the sample window. The Fourier transform performs a series of array multiplications that essentially down-convert (mix) each sine and cosine (real and imaginary) component to DC. The amplitude of each frequency component (bin) in the Fourier transform is then calculated by summing the power of the sine and cosine components. If these frequencies are coherent, this works very well. If there is not an exact match between input frequencies and those used in the algorithm, there are effects referred to as leakage. Leakage appears to raise the noise floor around a noncoherent frequency, and potentially masks details. With a large number of noncoherent frequencies, the transform becomes unusable.
If the frequencies used are not coherent, the use of windowing can reduce the leakage that results from an FFT performed on frequency components that are not an exact match for those frequencies that are used in the transform. Windowing involves first applying a symmetrical profile to the data set that tapers the weighting of the samples towards each end, reducing the error contribution of any discontinuity at either end of the sample set. The sample set can be viewed as a repeating waveform and a discontinuity would repeat at fS/NFFT. The windowing is akin to AM modulation, and hence has side lobes around each component.
A group of 32 capacitive sensors could be used for various tasks such sensing the position of some object routed through a series of sensors; measuring the flatness of a surface; or the dielectric constant of some material compared to reference material; or detecting the presence of objects in material handling devices.
Figure 3 and Figure 4 show the output of a 4096 point FFT performed on the output of two FIR filters processing the two data streams.
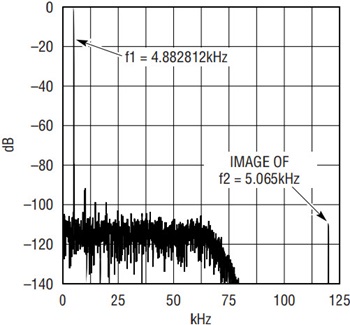
Figure 3. Primary measurement function, DC–50kHz.
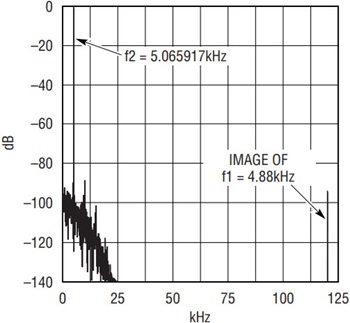
Figure 4. Secondary channel translated from 120kHz to 5kHz.
Figure 3 is the result of a 32 tap FIR low pass filter with –3dB at 50% Nyquist on the original sample set. Figure 4 is the result of inverting every other sample in another set, which is subsequently passed through an FIR filter with a corner frequency at 10% of Nyquist. In Figure 3 the first channel is at –4dBfs, and the secondary channel is at –15dBfs.
The signals that are processed in the secondary frequency range near Nyquist should be reduced in amplitude relative to the primary channel, in order to avoid reducing the dynamic range of the primary function.
This approach can be used for a large variety of secondary measurement tasks where the frequency range near Nyquist is suppressed by digital signal processing of the over-sampled signals.
Conclusion
The use of the LTC1864 for simultaneous acquisition of this type can provide a higher level of functionality without significant cost, or power implications. Portable or loop powered remote applications, constrained by a severely restricted power budget, can maintain the continuous sampling of the ADC while periodically using the secondary measurements at a low duty cycle or using a multiplexer to expand the number or measurements. The measurements in the secondary channels do not in this case disturb the deterministic operation of the primary channel.
Notes:
1 An FPGA can be a compact and inexpensive way of building a large number of phase lock loops in order to produce a reasonable collection of excitation frequencies that are all coherent.
This can be done by dividing the sample clock by 2N, where 2N is less than the size of the FFT, to produce a reference frequency (fREF) in a range that is noninterfering, and manageable in terms of VCO tuning range, and which also results in manageable loop filters. The VCO operates at an integer multiple of fREF. Subsequently, the output of the VCO must be divided by (FFT Size)/2N, where 2N is the same as above.
For example, for a 1024-point FFT, a divide by 8 of the sample frequency will produce 31.250 kHz from the 250kHz sample clock. This can be the frequency at which all the phase comparators operate. The phase lock loops would each have a VCO divided by an integral number related to the bin number. The output of each VCO would also have a divider at (1024/8) = 128 to produce the coherent excitation frequency. For example, for an excitation frequency 1 bin before Nyquist, the VCO would operate at 31.96875MHz, and the excitation frequency would be at 249.7558kHz. This frequency is not necessarily the best choice of frequency, it is just an example.
If the frequency range of interest of the primary function is limited to a few kHz—as is often the case with pressure, load, temperature, etc.—a range of frequencies that may be better suited to capacitive sensors could be used, or for example, in the range of 50kHz. For example, a group of 32 coherent frequencies, preferably falling in odd bin numbers, could be produced in the range of 53kHz–73kHz. The 3rd harmonics of this group will fall unobtrusively in the range of 94kHz–123kHz.
























