MEMS加速度计的振动校正
高性能MEMS加速度计为各种集成惯性测量的应用提供低成本解决方案。具体例子包括:导航和AHRS系统,用于机器健康状况检测的振动监控,基础设施的结构健康状况监控,以及用于平台稳定、井下定向钻探的倾斜监控、施工行业平路机和勘测设备的调平、吊车稳定系统吊杆倾角测量的高精度倾角计。在大多数此类例子中,加速度计会经受不同幅度的振动。这些应用的另一个不同方面是振动的频率成分。振动与传感器和系统误差源相结合可能导致振动校正,这是高性能加速度计的一个重要指标。本文说明MEMS加速度计中的振动校正是如何发生的,并讨论各种测量此参数的技术。作为案例研究,本文会讨论低噪声、低功耗加速度计ADXL355的振动校正。低振动校正误差以及所有其他特性,使这款器件成为上述精密应用的理想之选。
振动校正的来源
振动校正误差(VRE)是加速度计对交流振动(被整流为直流)的响应,表现为加速度计失调的异常偏移。在倾角计等应用中,这是一个重大误差源,因为加速度计的直流输出是目标信号,失调的任何改变都可能被错误地解读为倾角变化,导致误差一路向下传递,从而引起安全系统误触发、平台稳定或钻桅对准机制过度补偿等。
VRE高度依赖于加速度计所经受的振动特性曲线,不同应用施加于加速度计的振动模式会不同,因而VRE可能不同。振动校正有多种发生机制,本文讨论其中的两种。
非对称轨
第一种机制是非对称轨。重力产生一个静态1 g (9.8 m/s2)加速度场,当加速度计敏感轴竖直对齐时,其测量范围会有一个偏移。2 g满量程范围的传感器与重力加速度对齐时,将只能测量1 g峰值振动,否则响应会被削波。超过1 g的对称激励信号的平均值将不为零,原因是在经受额外1 g加速度的方向上,电平会被削波。
图1中,一个激励振动信号施加于2 g满量程传感器上。当振动为0.3 g rms(300到600样本之间)时,失调没有可观测的偏移。然而,当振动为1 g rms(600到1000样本之间)时,VRE约为–100 mg。

图1. ±2 g满量程范围的加速度计因为非对称削波而产生的振动校正图解
VRE可建模为一个截断分布的平均偏移,受加速度计满量程范围的限制。当传感器在1 g场中经受随机振动时,输入激励信号可建模为一个平均值μ= 1 g且标准差σ= X的正态分布,其中X表示输入振动幅度均方根值。传感器输出建模为双截断正态分布,输出值下界和上界分别为–R和+R,其中R为传感器的最大范围。此双截断正态分布的平均值计算如下:
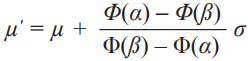
其中,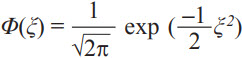 为概率密度函数,
为概率密度函数,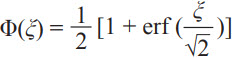 为其累积分布函数。α 和β 被定义为
为其累积分布函数。α 和β 被定义为![]() ,
,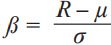 。这样VRE即为:
。这样VRE即为:
![]()
比例因子非线性误差
非线性误差是指工作范围内加速度计输出与最佳拟合直线的偏差。此偏差常常用满量程输出范围的百分比表示。加速度计的非线性误差可能引起VRE,如下所示:
描述加速度计非线性的常见模型是n次多项式。输出ao (LSB)可表示为输入ai (g)的函数:
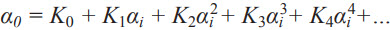
其中:
K0:失调 (LSB)
K1:比例因子 (LSB/g)
Kn:非线性的n次项系数,n = 2,3, … (LSB/gn)
考虑一个简单的正弦输入加速度:
![]()
此输入的时间平均值为零。加速度计的输出可表示为:

时间平均输出等于上式右侧所有分量的时间平均值之和。奇数次项的平均值为零。带入偶数次项的平均值 和
和  ,输出的时间平均值即为:
,输出的时间平均值即为:
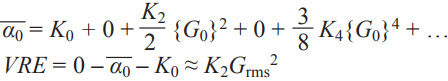
其中Grms为输入加速度的均方根值。上式说明,在一个正弦振动的情况下,二次非线性转换为直流失调的偏移 (K2Grms2)。项 ![]() 代表振动校正系数(VRC),单位为µg/g2-rms。
代表振动校正系数(VRC),单位为µg/g2-rms。
振动校正的幅度和频率相关性
振动幅度很小时,VRE以传感器非线性为主,可用VRC来表示: VRE = VRC × vib2rms。然而,当振动幅度大于满量程范围时,VRE往往以上一部分所述的非对称削波为主。另外,正如之前提到的,加速度计输出的任何非零失调也会引起非对称削波。大多数针对工业应用而设计的MEMS加速度计都会内置故障安全电路,在有很大振动时,它会关闭传感器偏置电路,防止检测元件受损。振动幅度很大时,此特性可能会在失调中进一步引起异常偏移,使VRE恶化。
由于各种谐振和器件中的滤波器,VRE常常具有很强的频率相关性。由于谐振器的两极响应,在传感器的谐振频率下,MEMS传感器谐振会放大振动,放大比率等于谐振品质因数,而在频率较高时则会抑制振动。谐振品质因数较高的传感器,振动幅度越大,其VRE也越大。由于高频带内振动的积分效应,较大的测量带宽也会引起较高的VRE。信号处理电路中实现的模拟和数字滤波器可抑制输出端的带外振动峰值和谐波,但对VRE没有明显作用,原因是振动输入被偶数次非线性整流为直流信号。
测量振动校正
一旦将加速度计部署于现场,便无法实时补偿VRE。在有些应用中,振动引起失调中出现较小直流偏移是可以容忍的,对此可以测量VRE以估计加速度计输出中的误差,从而确定VRE是否在允许限度内。在任何振动测量中,振动台和试验夹具必须平齐,并且必须使用精密振动台以抑制振动台跨轴振动、偏移和结构谐振引起的误差。另外,试验夹具必须具有适当的刚度,确保夹具谐振频率离加速度计带宽和振动曲线频段很远。较优夹具设计的最低谐振频率应当比最高振动频率高出大约50%。
正弦振动特性曲线
正弦振动方法是最常用且现有文献讨论最多的方法,已被纳入IEEE标准1293-1998。一般程序是将一个正弦振动输入施加于加速度计,然后测量失调偏移与均方根振动幅度(vibrms)的关系。VRC可以通过对此数据应用最小二乘法来估算:
![]()
由于可以很好地控制幅度,并且可以确保加速度计不会削波,因此通过这种方法能够精确测量VRC。这种测试还能用来识别并量化器件谐振对VRE的影响。然而,它一次只能测试一个频率,而要充分衡量传感器性能,必须分别测试加速度计带宽范围内的多个频率。
随机振动特性曲线
VRE也可以利用随机振动输入来测量。通常,实际的振动不像正弦振动特性曲线那样呈周期性或可预测,因此通过这种方法可以衡量加速度计在大部分应用中的性能。通过量化宽频率范围内宽带激励的失调偏移,这种方法更适合于同时纳入所有扰频并激励所有器件谐振。然而,它不保证峰峰值振动幅度,故而获得的VRE为频率范围上的平均值。
图2比较了配置为±2 g范围的ADXL355 Z轴传感器的截断平均值模型与实测VRE。测量中,Z轴与重力(1 g场)对齐,利用Unholtz-Dickie振动台施加一个随机振动特性曲线(50 Hz至2 kHz频段)。利用一个参考加速度计(PCB Piezotronics 352C23型)测量振动幅度;当振动幅度提高到满量程范围以上时,测量失调偏移。截断平均值模型(拟合到2.5 g截断)与测量结果拟合得很好。由于机械传感器开销和输出带宽限制(测量数据中的加速度计带宽为1kHz,但模型不考虑带宽),截断相对于设置的满量程范围预计会有偏差。当振动水平达到8 g时,±2 g范围的超范围保护电路就会激活。高斯分布振动的波峰因数约为3,因此超过2.5 g rms后,实测性能开始明显偏离模型。

图2. 截断平均值拟合与ADXL355实测振动校正的比较
影响VRE的其他因素
MEMS传感器谐振会影响加速度计的振动校正。高质量因数会导致频率接近传感器谐振频率的振动信号被放大,引起较大VRE。这可以通过比较ADXL355(±8 g范围、1 kHz带宽)的Z轴传感器与X轴和Y轴传感器的VRE性能得知;图3显示X轴和Y轴传感器的VRE在3 g rms左右达到峰值,因为其Q高于Z轴传感器。

图3. 在ADXL355的两个DUT中,高Q(X轴、Y轴)和低Q(Z轴)传感器的VRE比较
使用不必要的较大带宽时,也会导致加速度计对较高频率成分求均值,从而对VRE产生不利影响。图4反映了这一点,其比较了ADXL355 DUT(±2 g范围)的Y轴传感器在两种不同带宽设置下的VRE。125 Hz带宽设置的VRE显著低于1 kHz带宽设置的VRE。

图4. 1 g场中ADXL355的Y轴传感器(±2 g范围)在两种不同带宽设置(125 Hz和1 kHz)下的VRE
结语
为加速度计选择合适的带宽以抑制高频振动,可以避免很多振动相关问题。通过放大谐振时的振动耦合,包装因素(如封装和安装谐振)也会影响VRE。确保封装有适当的刚度,让封装和安装谐振频率位于加速度计带宽之外,是实现良好振动校正性能的关键。
总之,振动校正误差(VRE)是MEMS加速度计的一个重要指标,本文讨论了VRE的主要来源及相应的测量技术。设计利用MEMS加速度计在高振动环境中进行直流测量时,应当考虑这种效应。ADXL355提供出色的振动校正、长期可重复性和低噪声性能,并且尺寸很小。




















