LTspiceの優位性
アナログ設計技術者が回路の性能を予測する際、必ず頼りにするものがあります。それがシミュレーションです。当然のことながら、シミュレーションを実行するには、適切なシミュレータ(シミュレーション用のソフトウェア)が必要です。シミュレータの価値は、物理的な事象についていかに正確な数値によって表現できるかということと、いかに迅速に結果を提示できるかということにかかっています。シミュレーションによって得られた回路の性能と現実の回路の性能に大きな差があると、コストのかかるデバッグ作業を繰り返さなければならなくなるかもしれません。
アナログ回路のシミュレーションには、広くSPICE(Simulation Program with Integrated Circuit Emphasis)が使用されています。SPICEであれば、大信号に対する任意の回路の動作について完全に計算することができるからです。アナログ回路のシミュレーション結果が適切に得られるようにするために、SPICEでは、以下に示す3つの数値計算手法が使われています。
- ニュートン反復法:非線形素子を備える回路の振る舞いに関する解を求めるために使われます。
- 疎行列法:大規模な行列を現実のコンピュータのアドレス空間に格納するために使われます。
- 陰積分法:回路のリアクタンスによって導き出される微分方程式を積分するために使われています。
SPICEシミュレータによって正しい結果が確実に得られるかどうかは、上記の方法がいかに適切に実装されているかによって決まります。正しい結果が得られるという点で、LTspice IV(第4世代のLTspice)は他のSPICEシミュレータよりも優れています。本稿では、その理由について説明します。
ニュートン反復法
ニュートン反復法では、各種の非線形回路のI-V(電流‐電圧)曲線をテイラー級数として展開します。その際には、最初の2項だけを残し、得られた連立1次方程式を解くということが行われます。この連立1次方程式の解が、確かにテイラー級数が展開されたその点であったとします。その場合、テイラー近似解はその点で正しく、その近傍で正確であると言えます。したがって、その連立1次方程式の解は実際に元の非線形回路の正しい解であるということになります1。ニュートン反復法による計算が収束したということは、回路の正しい解が見つかったことが数学的に証明されたということを意味します。
ニュートン反復法の堅牢性は、次の2つによって決まります。すなわち、(1)すべての回路素子のI-V曲線において値と傾きが連続していること、(2)すべての非線形素子がコンデンサでバイパスされており、前の時間ステップの解が現時点のニュートン反復法の適切な開始点になることの2つです。これらの条件は、現実の回路であればどのようなものでも満たされることなのですが、通常、SPICEのプログラムではそうはなりません。その背景には次のようなことがあります。多くのSPICEシミュレータは、Berkeley SPICEをベースとしています。ただ、Berkeley SPICEの半導体デバイスのモデルには不連続性が存在します。その実装上の問題が、多くのSPICEシミュレータに波及しているということです。それに対し、LTspiceではそうした不連続性は発生しません。図1A、図1Bは、そのことを示す一例です。それぞれ、PSpice2とLTspiceで取得したダイオードのI-V曲線を表しています。これらのシミュレーションで使用したネットリストは次のようなものです。
* I-V discontinuity in PSpice diode
V1 N001 0 0
D1 N001 0 D
.dc V1 -.3 -.2 2u
.probe
.model D D(Is=10n)
.end
PSpiceによるシミュレーション結果を見ると、値と傾きの両方に不連続性が生じています。PSpiceによってシミュレーションを行った場合、ほとんどの半導体デバイスにおいてこのような不連続性が現れます。それに対し、LTspiceでシミュレーションを行った場合、半導体デバイスにおいてそうした不連続性が生じることはありません。


疎行列法
テイラー級数は多次元であり、回路内の未知の電圧ノードごとに1つの次元が対応づけられます。アナログICの場合、電圧ノードの数は10万にも達する可能性があります。そのため、10万×10万の導電率の行列、つまり倍精度の行列係数で言えば800億バイトものデータが必要になるかもしれないということです。64ビットのプロセッサでさえ、これほど多量のメモリにアクセスできるだけのアドレス・ラインは備えていません。ただ、ほぼすべての係数はゼロなので、それらは保存しなくて済みます。疎行列法では、ゼロではない要素のみを対象として追跡を行います。それにより、比較的小さなアドレス空間によって大規模な行列を解くことができます。
疎行列は、実際の回路の物理的な性質に起因して使われるようになりました。実際の回路では、ほとんどのノードは他の少数のノードに接続されているだけです。例として、網の目のような抵抗回路の導電率行列をすべて書き出すケースを考えます。その場合でも、各ノードは抵抗によって隣接するノードに接続されているだけなので、行列はほとんど対角成分になります。実際の回路では、接続密度は網の目の結び目ほど高くはありません。大規模なアナログ回路のまばらさは、ppmのレベルです。このまばらさのおかげで、コンピュータによって行列を解くことができるのです。アナログ回路に対するニュートン反復法は、疎行列法がなければ実行できません。
様々なSPICEシミュレータが提供されていますが、それらの最大の類似点はこの疎行列法を採用している点にあります。また、すべてのSPICEシミュレータはLU分解を採用しています。加えて、ほとんどのSPICEシミュレータはアカデミック向けに配布されているBerkeley SPICEのコードから派生した疎行列のライブラリを使用しています。そうしたシミュレータの一部は、高速SPICEとして市販されています。その種の製品については、SuperLU3のような拡張を施した疎行列のライブラリを使うことで改善が図られています。
基盤になるハードウェアのFLOP(浮動小数点演算)には理論限界が存在します。より優れた方法は、そのレベルでプロセッサによる演算を行うことです。ただ、問題になるのは、FPU(浮動小数点演算ユニット)が実際にFLOPを実行する時間よりも、FPUが数値データを取得するために要する時間の方が長くなることです。
通常、FPUのパイプラインは空の状態で動作します。あらゆるOSがメモリを動的に割り当てることから、そのような結果になります。シミュレータのプログラムが記述/コンパイルされた時点では、行列のデータを格納するメモリの位置は不明です。実行の段階になってから、シミュレータは関数呼び出しmalloc()によってメモリの割り当てを要求します。この関数により、シミュレータが行列のデータを安全に格納できるアドレスが返されます。人手によって各行列の要素に独自の名前を付けるのは不可能なので、配列が使用されることになります。つまり、シミュレータは、数は少ないものの規模のより大きいメモリを要求します。そして、個々の係数にはmalloc()が返すベース・アドレスからのインデックスが付加されます。シミュレータのコンパイル時にわかっているのは、行列の要素にアクセスするためのインデックスを作成する際に基準になるベース・アドレスだけです。そのアドレスを実行時に解決し、FPUに対してそのアドレスで指定されたデータを引き渡すためにかかる時間は、FLOPの実行に要する時間よりも長くなります4。計算に必要なデータのアドレスは、計算を実施する前にわかっていることが理想です。そうすればデータを効率的に取得できます。つまり、FPUはアドレスが明確になるまでにかかる時間を待つ必要がなくなります。
LTspiceでは、行列のメモリが割り当てられてmalloc()から返されたアドレスが明らかになった後、セルフ・オーサリング・アセンブリ言語のソースを実行時に書き込みます。そのため、FPUにデータを引き渡す際に生じるオーバーヘッドを排除できます。このレイト・オーサード・コード(late-authored code)により、行列の要素の具体的なアドレスをコードに基づいて解決することができます。LTspiceが備えるアセンブラとリンカによってコードがアセンブル/リンクされると、データを効率的にロードし、パイプラインが満杯の状態でFPUを動作させることができます。LTspiceは、セルフ・オーサリング、セルフ・アセンブリング、セルフ・リンキングという疎行列用のソルバを実装しているという点で他に類を見ないものです。それにより、他の手法を採用したシミュレータよりもはるかに優れた性能が実現されています。
陰積分法
アナログ回路のシミュレーションには、コンデンサとインダクタンスの挙動を追跡するために、微分方程式の数値積分を行う機能が必要になります。各種SPICEシミュレータの間の最も大きな違いは、微分方程式を積分するために利用できる方法にあります。
数値積分には誤差が伴います。アナログ回路のシミュレーションでは、多くの時定数について把握するために積分を実施しなければなりません。exp(-[定数]×[時間])のような形の解を持つ微分方程式を積分する場合、積分法と呼ばれる数値計算法を使用しない限り、誤差が無限大まで累積されてしまいます5。陰積分法を利用しなければ、SPICEによってトランジェント解析を行うのは不可能でしょう。
またSPICEでは2階積分が使用されます。ほとんどのSPICEシミュレータはBerkeley SPICEをベースとしており、Gear積分法と台形積分法(trap)6という2つの2階陰積分に対応しています。台形積分法は、Gear積分法よりも高速かつ高精度です。但し、台形積分法では数値的な面で悪影響が生じる可能性があります。それは、真の連続時間動作とは異なり、離散時間ステップの積分の解は時間ステップの間で発振してしまうというものです。このことから、各台形に正しい積分面積が含まれている場合でも、ユーザがシミュレータの正確さについて疑いを持ってしまうという結果になる可能性があります。.
台形積分法で生じるリンギングは、アナログ回路の設計者にとって許容できないものになると考えられます7。そのため、台形積分法は、商用のSPICEシミュレータの1つであるPSpiceでは採用されていません。PSpiceでは、利用可能な唯一の選択肢として、低速で精度の低いGear積分法が使われます。
Gear積分法であれば、数値的なリンギングは減衰させることができます。但し、物理的なリンギング(実際に回路で生じるリンギング)も含めてすべてのリンギングが減衰します。そのため、実際には発振によって誤動作する回路のシミュレーションを行ったのに、完全に安定した状態で適切に機能するという結果が得られてしまうことがあります。このような状況は、実際の回路の不安定性が減衰されて数値的には存在しなくなることによって生じます。このことによって、次のような事例が引き起こされたことがあります。それは、PSpiceによってICに集積する回路のシミュレーションを実施し、レイアウトを行い、製造した結果、その時点になって問題が見つかったというものです。PSpiceのGear積分法によってシミュレーションを行ったために不安定性が見逃され、製造済みのICが適切に動作しなかったという悲惨な結果になってしまったのです。回路の不安定性を取り除いて本来の機能を実現するためには、フォトマスクの修正をはじめとする追加の作業が必要になります。つまり、かなりの時間と費用が浪費されるということです。
Gear積分法による誤差は、原理的にはIC設計者が最大時間ステップを小さく設定することによって低減することができます。しかし、これは現実的な解決策にはなりません。その理由は、時間ステップを小さくすることによりシミュレーション速度が遅くなることに加え、時間ステップが十分に小さく設定されているということを保証する方法が存在しないからです。
PSpiceのドキュメントを見ると、「PSpiceでは改善/修正を図ったGear積分法を採用している。Berkeley SPICEに実装されたGear積分法を使用する場合と比べて誤差を小さく抑えるには、十分に小さな時間ステップを選択すればよい」という主旨の記載があります。
しかし、この方法を適用しても良好なシミュレーション結果が得られないことは少なくありません。簡単な回路を作成し、PSpiceによってシミュレーションを実施したところ、数値積分の結果が、デバイスの実測によって得られる真の解から大きくずれていたというのはよくあることです。ここで、図2の回路について考えてみます。この回路では、並列タンク回路にPWL関数で制御する電流源を並列に接続しています。この電流源は、最初の0.2ミリ秒間だけ電流スパイクをアサートし、その後は電流値をゼロに保持します。そうすると、このタンク回路では電流スパイクによって励起された発振が生じ、その後は一定の振幅でリンギングするという結果になるはずです。

この回路のネットリストは、以下のようになります。
* Gear (PSpice) integration error
L1 N001 0 50m
I1 0 N001 PWL(0 0 .1m .1 .2m 0)
C1 N001 0 .1u
.tran 1 1 0 50u
.probe
.end
図3Aに示したのは、PSpiceによるシミュレーション結果です。同シミュレータの改善/修正を図ったGear積分法(以下、修正Gear積分法)により、リンギングが人為的に減衰されています。一方、図3Bに示したのは、LTspiceによるシミュレーション結果です。ご覧のように、正しい解が即座に出力されていることがわかります。PSpiceにおいては、最大時間ステップ(.tran文の4番目の数値)を小さな値に設定するだけで誤差が低減されています。図2の回路は、PSpiceの修正Gear積分法を使って解を得なければならないほど複雑なものではありません。しかし、多くの異なる時定数を備える回路では、最大時間ステップを小さくするにつれて、PSpiceで確実に解を得るのは基本的に不可能になります。適切な結果を得るには、どのようにして解が収束するのか、手作業によって調べなければなりません。
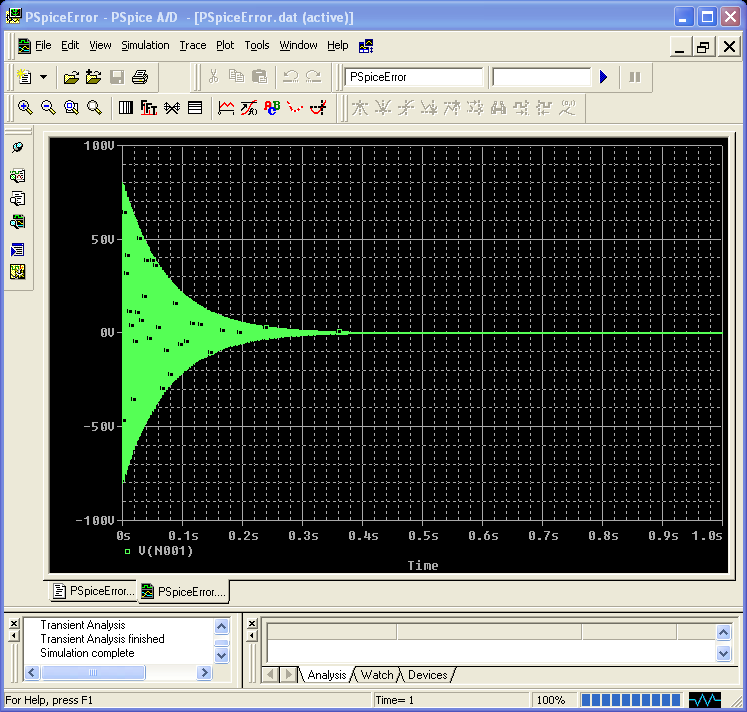

図3Aは、PSpiceのGear積分法を適用した結果です。ノードが1つしかない簡単な回路ですが、2つのリアクタンスに関する積分が明らかに正しく行われていません。Gear積分法によって生じる誤差の性質上、現実とは異なりシミュレーション上では回路が安定しているように見えます。図4に示した回路は、この誤差の影響を実際の例を基にして確認するためのものです。この回路は、オーディオ用のパワー・アンプとして設計されました。ただ、補償用のコンデンサC2の値が小さすぎるので安定した動作は得られません。

PSpiceでシミュレーションを実施すると、この回路は安定しているという誤った結果が得られます。それに対し、LTspiceによってシミュレーションを行えば、正しい結果が提示されます。なお、シミュレーションでは以下に示すネットリストを使用しました。
* Unstable Power Amplifier
Q5 N001 N006 N007 0 Q3904
Q7 N001 N007 OUT 0 Q2219A
Q8 OUT N013 N014 0 Q2219A
Q6 N013 N012 OUT 0 Q3906
V1 N001 0 10
V2 N014 0 -10
R11 N012 N014 5K
R14 OUT 0 8
R9 N006 N008 2K
R10 N008 N012 1K
Q4 N006 N008 N012 0 Q3904
Q1 N005 N009 N011 0 Q3904
Q2 N002 N010 N011 0 Q3904
R3 N011 N014 1K
Q3 N006 N004 N003 0 Q3906
R6 N010 0 20K
R7 OUT N010 200K
V3 IN 0 pulse(0 .1 0
+ 5u 5u 50u 100u)
R8 N001 N003 100
R4 N004 N005 10K
C2 N006 N004 10p
R13 N013 N014 1K
R12 N007 OUT 1K
C3 N006 N012 .001u
Q9 N005 N002 N001 0 Q3906
Q10 N002 N002 N001 0 Q3906
R2 IN N009 9.09K
.tran 100u 100u
.model Q3904 NPN(Is=1E-14 Vaf=100
+ Bf=300 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4p Cje=8p Rb=20 Rc=0.1
+ Re=0.1 Tr=250n Tf=.35n
+ Itf=1 Vtf=2 Xtf=3)
.model Q3906 PNP(Is=1E-14 Vaf=100
+ Bf=200 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4.5p Cje=10p Rb=20
+ Rc=0.1 Re=0.1 Tr=250n
+ Tf=.35n Itf=1 Vtf=2 Xtf=3)
.model Q2219A NPN(Is=14.34f
+ Xti=3 Eg=1.11 Vaf=74.03
+ Bf=255.9 Ne=1.307 Ise=14.34f
+ Ikf=.2847 Xtb=1.5
+ Br=6.092 Nc=2 Isc=0 Ikr=0
+ Rc=1 Cjc=7.306p Mjc=.3416
+ Vjc=.75 Fc=.5 Cje=22.01p
+ Mje=.377 Vje=.75 Tr=46.91n
+ Tf=411.1p Itf=.6 Vtf=1.7
+ Xtf=3 Rb=10)
.probe
.end
図5Aは、PSpiceによるシミュレーションの結果です。ご覧のように、この回路によって安定した動作が得られるという誤った結果が示されています。一方、図5BはLTspiceによるシミュレーションの結果です。ご覧のとおり、発振を起こしていることがわかります。図5Bの結果の方が、実際の回路に近い正しいものだと言えます。このシミュレーションでは、大信号のトランジェント解析によりステップ応答を確認しています。PSpiceによるシミュレーションでも十分に小さい時間ステップを設定すれば、現実に近い結果を得ることができます。このことから、PSpiceはトランジスタに関する方程式を正しく解釈していることがわかります。ただし、微分方程式を基に正しく積分が行われているわけではないということも明らかになりました。


必要なのは、台形積分法を使用した場合の速度と精度を確保しつつ、リンギングによる悪影響が及ばないようにすることです。その方法を追求する上で、PSpiceでは、Gear積分法を使用しつつ適切な時間ステップを選択することで台形積分法によって生じるリンギングを排除できるようにしました。別の手法として、台形積分法のデチューン版を使用してリンギングを減衰させつつ、回路の正しい動作を模擬し、うまくいけば許容できるレベルの小さな誤差しか生じないようにするというものも存在します。ドキュメントには記載されていませんが、trapdampというオプションを使用することでLTspiceの台形積分法をデチューンすることができます。この方法は、以下のSPICEディレクティブを回路図に記述することで利用可能です。
.options trapdamp=.01
いろいろと試してみれば、HSPICE8の積分動作を再現するtrapdampの値を見いだすことができる可能性もあるでしょう。しかし、このオプションを使用することはお勧めしません。このオプションを使用すると、実際の回路で生じるリンギングも減衰するからです。そして、何よりもLTspiceを採用すれば、このようなオプションを使用する必要がないからです。LTspiceは、より優れた方法を採用しており、台形積分法に伴うリンギングを除去できるようになっています。
LTspiceは、改善/修正を図った台形積分法(以下、修正台形積分法)を採用しています。それにより、台形積分法の速度と精度を維持しながらリンギングによる悪影響を抑えています。この修正台形積分法は、筆者が考案したものであり、LTspiceに適用したことで広く利用されるようになりました。筆者はこれこそがアナログ回路の微分方程式を積分するための最良の方法だと思っています。ただ、筆者が知る限り、他のSPICEシミュレータではこの方法は採用されていません。繰り返しになりますが、筆者の考えとしては、この修正台形積分法が回路設計向けに推奨できる唯一の方法です。なお、LTspiceでは、台形積分法やGear積分法を含む既知の方法も使用できるようになっています。ただ、それは他のSPICEシミュレータによる誤った結果を再現するためのものです。同じモデルを使用しても、積分方法が異なれば、それだけで大きな差異が生まれるということを確認することができます。
図3Bに示した結果は、LTspiceで修正台形積分法を使用して取得したものです。数千サイクルにわたりリンギングが発生した後も、その振幅に変化はありません。これは、LTspiceの修正台形積分法を使用した場合、人為的な数値的減衰は発生しないということを表しています。図5Bの結果も、LTspiceの修正台形積分法を使用して取得したものです。先述したとおり、図4に示したパワー・アンプの不安定性が適切に表現されています。
LTspiceの修正台形積分法を使用すれば、もともとの台形積分法を使用した場合に発生するリンギングを排除できます。このことを示すためには、台形積分法を使用した場合にリンギングが発生しやすい回路が必要です。台形積分法によってリンギングが発生するのは、離散時間ステップの2階積分では連続時間での回路の動作を正確に表現することが困難なケースです。この問題は、時間ステップと積分の階数制御を慎重に選択することで軽減または排除できます。

LTspiceは、ここ10年間で最も広く使用されているSPICEシミュレータです9。その間に、数多くの回路を対象としてシミュレーションが実施されました。その結果、台形積分法によって発生するリンギングを回避するための多くの知識がソルバの形でライブラリ化されています。そのため、リンギングが発生する例を取り上げるためには、少し工夫が必要になります。図6の回路では、異常なサイズのMOSFETを使ってインバータを構成しています。その結果、非線形性が高いゲート容量が存在する状態になっています。このようにすることで、通常の台形積分法を使用するとリンギングが発生します。具体的には、ゲートを駆動する電流I(V1)にリンギングが現れます。


図7A、図7Bは、台形積分法とLTspiceの修正台形積分法を比較するためのものです。いずれの図についても、上側のプロットは下側のプロットの一部を拡大したものです。図7Aの上側のプロットを見ると、リンギングがはっきりと確認できます。LTspiceでこの結果を再現したい場合には、「Control Panel」の「SPICE」ペインに移動し、デフォルトの「modified trap」の代わりに「trapezoidal」を選択してください。
このシミュレーションで使用したネットリストは以下のとおりです。
* Trap Ringing Example
V2 N001 0 3.3
V1 N002 0 PULSE(0 3.3 1n 1u)
M1 OUT N002 N001 N001 P
M2 OUT N002 0 0 N
.tran 0 1.2u 0 .1n
.model N NMOS(Tox=20n Vto=.5
+ Gamma=.5 UO=650 Rs=10)
.model P PMOS(Tox=20n
+ Vto=-.5 Gamma=.5 UO=650
+ Rs=10)
.probe
.end
なお、ほとんどのSPICEシミュレータでは、上記の例を意図したように動作することはありません。なぜなら、ほとんどのSPICEシミュレータは、このタイプのMOSFETにMeyer容量モデルを採用しているからです。同モデルでは電荷が保持されず、短チャンネルのトランジスタでは不正確な結果になるため、1990年代ごろからあまり使用されなくなりました。
LTspiceとPSpiceでは、同モデルがYang-Chatterjee電荷モデルに置き換えられています。LTspiceでもPSpiceでも、電荷蓄積の式については更新された同じものを使用しているので、同様の結果が得られるはずです。しかし、実際に両シミュレータを比較すると、図8に示すように、PSpiceでは著しく誤った結果が出ることがわかります。但し、PSpiceのシミュレーションに見られる発振は、台形積分法によって生じるリンギングが原因で発生しているのではありません。この発振は時間ステップ間では発生していませんし、そもそもPSpiceでは通常の台形積分法を使用していないからです。これについては、おそらくPSpiceのYang-Chatterjee電荷モデルの実装に原因があると考えられます。Yang-Chatterjee電荷方程式を容量で微分する際の誤差に起因して、このような結果が出ていることはほぼ間違いないでしょう。


まとめ
LTspiceは、最初に開発されたSPICEシミュレータではありません。また、無償で利用できる唯一のSPICEシミュレータでもありません。しかし、最も広く利用されている最も優れたSPICEシミュレータだと言えるでしょう。
SPICEでは、ニュートン反復法、疎行列法、陰積分法が中核的な数値計算法として使用されます。シミュレーションの堅牢性、速度、完全性が優れているか否かは、これらの計算法をいかに適切に実装しているかということにかかっています。
SPICEシミュレータについては、設計者から、回路の動作を正しく解くことができるものだという信頼を得る必要があります。そのためには、ソルバによって中核となる数値計算法を正しく実行できるようにしなければなりません。LTspiceであれば、それらの計算を適切に実施できます。その意味で、LTspiceは他のどのSPICEシミュレータよりも優れていると言えます。
注)
1 そうでない場合、連立1次方程式の解は反復用のステップとして使用されます。元の非線形回路は、この解に関する新たなテイラー級数として再度展開されます。その際にも、最初の2項だけを残し、得られた連立1次方程式が解かれます。このプロセスは、正しい解が得られたと証明されるまで繰り返されます。
2 PSpiceはCadence Design Systemsの商標です。図1Aのスクリーン・ショットは、PSpiceのバージョン9.2に対応しています。
3 行列が疎であるほど、対角行列(つまり、解かれた行列)に近い行列として記述することができます。アナログ回路に対応する行列は非常に疎なので、SuperLUでLU分解を改善しても、速度の面では期待するほどの効果は得られません。
4 行列において未知の要素をなくすためには、ほとんどの場合、加算、減算、乗算が必要になります。これらの命令に必要なのは、わずか3つの潜在的なクロック・サイクルだけです(3サイクルをはるかに超えるクロックが必要な除算もありますが、1つの未知の要素をなくすためには1回の除算しか必要ありません)。インデックスを作成する際に基準となるベース・アドレスによってのみ知ることができるデータを取得するためには、3クロック・サイクルよりもはるかに長い時間がかかります。
5 これに関する文献の中には、十分に小さい時間ステップが保証されている場合、数値解は特異解にはならないと指摘しているものがあります。ただ、実際には、陽積分法と制限された時間ステップによる方法では、無限の精度で数値積分を行えない限り、適切な結果は得られません。丸め誤差によって誤差が無限大まで累積されることはありません。無限大になるのは、サンプリングされた有限個の差分によって導関数が近似されることによるものです。アナログ回路用の一般的なシミュレータの中に、陽積分法を採用して成功を収めているものは存在しません。
6 SPICEでは1階積分が実施されることもあります。例えば、独立した電圧源や電流源の区分線形関数を使用する場合や、パルス関数において2つの直線区間を遷移する場合など、既知の不連続1階時間微分を伴う事象が発生することがあります。そうすると、ほとんどのSPICEシミュレータでは、遷移時に回路のリアクタンスの1階積分が行われます。Gear積分法と台形積分法の1階積分バージョンは、どちらも後退オイラー法に相当します。
7 SPICEシミュレーションの価値を貶めるような文献が存在することから、SPICEに対して疑心を抱いているユーザもいます。
8 HSPICEはSynopsysの商標です。
9 LTspiceは毎分4回ダウンロードされています。あらゆるシミュレータの最大のユーザ・グループでも話題として取り上げられています。他のSPICEシミュレータを販売する各社の担当者との私信に基づくと、LTspiceの配布数/利用数は、他のSPICEシミュレータと比べて3桁多いと考えられます。