LTspice上でラプラス変換を利用し、伝達関数のモデルを構築する
概要
フィルタや電源などの電子システム/制御システムを設計する際には、伝達関数が利用されます。そして、伝達関数の解析を周波数領域で行う場合には、ラプラス変換を利用すると便利です。本稿では、LTspice®を使って伝達関数のモデリングを実施する方法を説明します。いくつかの現実的な例を基に、モデルの応答と現実の回路の応答を比較しながら検討を進めることにします。また、本稿の内容を実際の設計に活用できるように、数多くのサンプル・ファイルを提供します。
はじめに
伝達関数は、システムの入力に応じて出力がどのように変化するのか解析するために使用されます。システムの出力の例としては、抵抗分圧器の出力電圧や、アクセルを踏み込んだときの車速などが挙げられます。システムの解析を実施する際には、入力に対する出力の振幅と位相の変化を周波数領域で確認するということがよく行われます。その際、よく使用されるのがラプラス変換です(以下参照)。

ラプラス変換について数学的または直感的に説明する文献は、数多く提供されています。本稿では、ラプラス変換は、システムのゲイン、周波数、位相、指数関数的応答を調べるための単なる数学的な手段だと見なして話を進めることにします。
伝達関数の基本的な概念は、図1のように表すことができます。

図1. 伝達関数の概念

図2. 2種類の回路とその信号波形。抵抗分圧器でもRC回路でも、f = 1kHzにおいて振幅は1/2になります。RC回路では遅延も生じます。
図2に、伝達関数について理解するための回路例を示しました。この回路には、2つの出力が存在します。したがって、それらに対応する伝達関数も2つ存在します。まず、抵抗分圧器の伝達関数は、次のような単純なものになります。

抵抗R1とコンデンサC1から成るRC回路はもう少し複雑です。その伝達関数は、以下のようになります。

このような形で伝達関数を記述すれば、極とゼロについて把握することができます。この例の場合、ωp = 1/RCに極が1つ存在します。ここで、図2のグラフをご覧ください。RC回路の出力(赤色)は、1kHzの正弦波です。その振幅は、抵抗分圧器の出力振幅と等しいものの、位相は遅れていることがわかります。伝達関数にラプラス変換を適用すれば、RC回路のゲインと位相が周波数に応じてどのように変化するのか把握することができます。図2の回路図に対応するサンプル・ファイル(Simple_RC_vs_R_Divider.asc1)は、当社のサイトからダウンロードすることができます(以下、各サンプル・ファイルのリンクは、稿末の参考資料のセクションにも示してあります)。
LTspiceにおけるラプラス変換の使い方
LTspiceでラプラス変換を利用するには、まず、回路図上に電圧制御電圧源(Voltage Dependent Voltage Source)を配置します。その際には、図3に示すダイアログ・ボックスを使用します。

図3. 電圧制御電圧源の配置に使用するダイアログ・ボックス
次に、配置した電圧源を右クリックし、Component Attribute Editorを開きます(図4)。同エディタが開いたら、Valueフィールドにおいて「Laplace =」の形で式を入力します。このとき、式には複素変数sが含まれていなければなりません。

図4. Component Attribute Editorの操作画面。Valueフィールドに式を入力します。
図4の式において、CとRについては、.stepコマンドで値を変化させられるようにするために波括弧で囲んでいます。
図5に、RC回路のステップ応答のシミュレーション結果を示しました。併せて、ラプラス変換を使用して記述した、それと等価な伝達関数のシミュレーション結果も示しています。これらを見れば、両者の出力として同様の波形が得られることがわかります2。

図5. RC回路のシミュレーション結果。回路図の下側には、RC回路と等価な伝達関数を配置しています。この伝達関数は、ラプラス変換を使用して記述しています。併せて、そのシミュレーション結果も示しました。
なお、伝達関数の記述が長くなる場合には、対応する括弧を自動的にハイライト表示してくれるコード・エディタ(テキスト・エディタ)を使用するとよいでしょう(図6)。エディタ上で式を入力/コピーし、LTspiceのダイアログ・ボックスにペーストするといった具合です。

図6. テキスト・エディタのハイライト表示機能
極とゼロについてのおさらい
以下に示すのは、伝達関数の例です。

この式には、ωp0/sという項があります。これは、原点に極が存在するということを意味します。以下、この極を原点極と呼ぶことにします。原点極が存在するというのは、積分器が存在することと同義です。つまり、低い周波数において非常に高いゲインを供給するために使うことができます。その結果、制御システムにおいて、定常状態の誤差を除去することが可能になります。具体的には、原点極により、90°の位相遅れが生じ、-20dB/decのゲイン応答が得られます。ωp0は、原点極によってゲインが0dBになる周波数を表します。
分子と分母の根を導き出せば、ゼロと極の周波数を求めることができます。それらの根の大きさ(絶対値)が、極とゼロの周波数です。ゼロの周波数の周辺では、位相は90°進み、ゲインは増大します。極の周波数の周辺では、位相は90°遅れ、ゲインは低下します。
続いて、以下の伝達関数について考えます。

最初のsの項は、原点にゼロが存在するということを意味します。以下、このゼロを原点ゼロと呼ぶことにします。原点ゼロは、純粋な微分器に相当します。位相は90°進み、ゲインは周波数が高くなるほど増加して周波数ωz0で0dBになります。
図7に示したのは、様々な極とゼロをLTspice上で表現した例です。それぞれ1kHzの周波数に対応しています。ゲインと位相のシミュレーション結果は、図8のようになります。図7の回路のサンプル・ファイルは、PoleZeroExamples.asc3として用意しています。

図7. 極とゼロの表現

図8. 極とゼロのゲインと位相(周波数はすべて1kHz)
モデルと現実の回路の比較
上述したように、LTspiceを使えば伝達関数のモデリングが行えます。この手法を活用すれば、モデル化されたコンポーネントから成る大きなライブラリを構築できます。最初の例として、比例ゲインを与える反転型のオペアンプ回路を取り上げます。その伝達関数は、理想的にはH(s) = -Rp/Riとなります。つまり、入力電圧にゲインを乗じ、位相を180°シフトした値が出力されるはずです。しかし、現実の回路(オペアンプ「LT6015」を使用)では、図9のような結果になります。これを見ると、約320kHzにおいてゲインは理想値から3dBロールオフし、位相も大きくずれています。図9の回路のゲインは-10V/Vで、LT6015のゲイン帯域幅は3.2MHzです。そのため、このような結果になります。

図9. 比例ゲインを実現する伝達関数と現実のオペアンプ回路
LTspiceでは、波形ビューワに解析用の式を入力して結果を表示することができます。そこで、理想的な式と現実のオペアンプ回路のゲイン/位相の差を確認するために波形を追加してみましょう。これは、波形ビューワ上を右クリックし、「Add Traces」を選択することによって行えます。ここで、一方のノードの電圧で他方のノードの電圧を除算する式を追加します。つまり、V(vout_pro)/V(vout_laplace)という式を追加するということです(図10)。
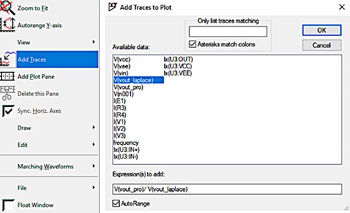
図10. 式の入力。この式によって得られる波形を追加で表示できます。
図11に示したのが、上記の操作を行った結果です。ご覧のように、ゲインと位相を比較することができます。このグラフから、低い周波数領域では、ゲインの差は0dBで、位相のずれも生じないことがわかります。図9に対応するサンプル・ファイルは、ProportionalGain.asc4です。

図11. 2つの波形の表示結果。2つの出力のゲインと位相を比較しています。
RLC回路として構成した2次システム
続いて、RLC回路として構成した2次システムを例にとります。2次システムについては、稿末に示した参考資料5をご覧ください。
2次システムの伝達関数は、次のようになります。

LRC回路として実装した場合、次のような式が成り立ちます。

図12に示したのは、LTspice上で構成した回路と伝達関数です。この例の場合、回路で使用するR、L、Cの値を指定することができます。伝達関数では、減衰係数ζと共振周波数ωnを指定することが可能です。

図12. RLC回路として構成した2次システム
この2次システムの周波数応答を図13に示しました。ご覧のように、一般的に望ましくないとされるピーキングが発生しています。例えば、降圧レギュレータ向けにEMI(電磁干渉)対策用のフィルタを設計する場合には、このようなピークを減衰させなければなりません。図12の回路のサンプル・ファイルをLRC_AC_Analysis.asc6として用意しました。

図13. 図12のRLC回路の周波数応答
微分器と安全
図14に示したのは、微分器の回路/伝達関数とそれぞれのシミュレーション結果です。

図14. 微分器の回路/伝達関数とシミュレーション結果
ご覧のように、原点ゼロが存在することから、周波数に対して20dB/decでゲインが増加します。微分器は、周波数の高い信号に対する応答を高めるために使用できます。実際には、純粋な微分器ではなく、安全極を追加したものが使われます。安全極を追加する目的は、システムが周波数の高いノイズに過敏に反応しないようにすることです。このオペアンプ回路では共振のピークが生じていることにも注目してください。このピークは、システムを制御する際に問題になる可能性があります。
この回路のゼロ(ゲインが0dBと交差する点)は、以下の式で求められます。

ここでは、上記の5倍の周波数に安全極を配置することにします。図15に示したのが、安全極を追加した微分器です。その周波数は、5×159Hz = 796Hzに設定しています。現実の回路では、入力コンデンサの1/5の値の帰還コンデンサを付加しています。伝達関数は、次のようになります。

ここで、ωz = 1/RpCd、ωp = 1/RpCiです。図15の右側に示したシミュレーション結果から、安全極により、その極周波数に近づくにつれてゲインと位相の値が低下することがわかります。また、オペアンプに起因するピーキングも抑えられます。
FOPDモデルの活用
システムの動作をモデル化する場合には、FOPD(First-Order Plus Delay)モデルを利用すると便利です。FOPDモデルについて簡単に説明すると、固定の遅延、フルスケールの応答、時定数でプロセスを表現したものということになります。詳細については、稿末の参考資料7をご覧ください。ラプラス変換を用いて固定の遅延を表現すると、以下のようになります。

時定数は、1 - 1/e = 63.2%と定義されます。FOPDモデルは次のようになります。

ここで、変数/定数の意味は以下のとおりです。
kp:フルスケールの出力
τF:時定数
θF:遅延時間
図16は、フルスケールが100、時定数が10秒、遅延が1秒のシステムの伝達関数です。t = 1〔秒〕でステップ信号を印加すると、t = 12〔秒〕で出力は63.2Vになります(図17)。このシミュレーションに対応するファイルはFOPD.asc8です。

図16. FOPDモデルを採用した伝達関数

図17. 図16のモデルのステップ応答
LTspiceによる補償回路の設計
制御システムの設計には、いくつもの学術分野にまたがる豊富な知識が必要になります。クローズドループ制御を行うシステムでは、補償回路が重要な要素になります。制御するシステムの伝達関数が明らかになったら、ゲインと位相の調整を行うための補償回路を設計することになるでしょう。その目的は、クローズドループの安定性と性能を確保することです。
タイプ2aの補償回路
多くのシステムでは、タイプ2aの補償回路を適用することによって目標を達成できます。タイプ2aの補償回路には、原点極(積分器)とゼロが存在します。負のフィードバックによる180°の位相遅れに加え、原点極によって更に90°の固定の遅延が追加されます。また、ゼロを配置することにより、追加された90°の位相シフトは高い周波数領域においては排除されます。特定の周波数においてどれだけの位相シフトが得られるようにするかを決定し、それに応じてゼロを配置します。

図18. タイプ2aの補償回路を適用したオペアンプ回路
図18に示したのは、オペアンプを使用した制御回路にタイプ2aの補償回路を適用した例です。タイプ2aの補償回路の伝達関数は、以下のようなものになります。

原点極の周波数はωp = 1/R2Ci、ゼロの周波数はωz = 1/R1Ciです。
この例でも、オペアンプの影響は明らかです。周波数が高くなると、ゲインと位相の両方が理想の値から外れてロールオフしていきます。図18の回路のサンプル・ファイルは、Type2a.asc9です。
タイプ2の補償回路
タイプ2の補償回路は、原点極ならびに極とゼロのペアで構成されます(図19)。

図19. タイプ2の補償回路を適用したオペアンプ回路/伝達関数
その伝達関数は、以下のようになります。

極とゼロは以下のようになります。
ここで、設計者はジレンマに陥ります。RsとCsの値は、極とゼロの両方に影響を及ぼします。また、極とゼロをどこに配置するのかという問題も解決しなければなりません。稿末の参考資料17では、具体例を基にこの設計プロセスについて詳しく解説しています。本稿では、その方法を適用したLTspice用のサンプル・ファイルとしてType2_autoCalcs.asc10を用意しました。図20は、このサンプルの出力を示したものです。10kHzにおいて、10dBの減衰と30°の位相の進みを実現するという目標が達成できています。この例でも、高い周波数領域において、理想とは異なる現実のオペアンプの影響が現れています。

図20. タイプ2の補償回路を適用した場合の周波数応答
タイプ3の補償回路
タイプ3の補償回路は、図21のようなものになります。

図21. タイプ3の補償回路を適用したオペアンプ回路
ご覧のように、その伝達関数はより複雑です。これは、位相をより大きく進めたい場合に使用します。この構成では、まず負帰還によって180°の位相遅れが生じます。ただ、ゼロが2つ存在するので、位相は180°進む可能性があります。2つの極は、高い周波数領域におけるゲインと位相をロールオフするために配置します。伝達関数は、以下のようになります。

極とゼロは、以下のようになります。

タイプ2の補償回路の場合と同様に、極とゼロの位置を選択して、RsとCsの値を計算するプロセスが必要です。参考資料17では、その設計プロセスについても説明しています。ここでは、その方法を適用したLTspice用のサンプル・ファイルとしてType3_autoCalcs.asc11を用意しました。このサンプルの出力は、図22のようになります。ご覧のように、5kHzにおいて10dBの減衰と145°の位相の進みを実現するという目標を達成できています。この例でも、高い周波数領域では、現実のオペアンプの影響が現れています。

図22. タイプ3の補償回路を適用した場合の周波数応答
時間領域における原点極
ここまで、回路素子とラプラス変換を使用してLTspice上で伝達関数を表現する方法を説明してきました。使用した例は、すべて周波数領域のものでした。そうなると、次は伝達関数を時間領域で解析したいと考えるのが自然な流れです。つまり、ステップ応答を確認できるようにしようということです。
そのためには、原点極とその表現方法の問題を解決する必要があります。原点極(つまりは純粋な積分器)の伝達関数はH(s) = 1/sです。この伝達関数は、周波数領域であれば正しく機能します(図23)。しかし、時間領域ではエラーが発生します(図24)。

図23. 原点極のAC解析。正しく実行されています。

図24. 原点極のトランジェント解析。エラーが発生しています。
この問題を回避するには、電圧制御電圧源の代わりに、ビヘイビア電圧源とidt関数を使用します。つまり、図25のような回路を用意します。この図には、帰還システムの一部も示されています。そこでは、セットバックと静的帰還電圧の比較が行われます。この回路のサンプル・ファイルを、OriginPole_TransientAnalysis_idt.asc12として用意しました。

図25. 時間領域でも適切に動作可能な構成
フィルタの設計
アナログ・デバイセズは、「リニア回路設計ハンドブック」を提供しています13。これは、当社がリリースしている膨大な学習用リソースのうちの1つです。その第8章には、アナログ・フィルタに関する説明があります。そこで紹介されている各種フィルタのラプラス表現を、Laplace_Filters_LinearSystemsBook.asc14というサンプル・ファイルとして用意しました。併せて、アクティブ・フィルタの設計を支援する「Precision Toolbox」のフィルタ設計のセクションも参照してください15。
まとめ
本稿では、集中素子表現とラプラス変換に基づく式を比較しながら、伝達関数の活用方法について説明しました。紹介した数多くの例は、机上で学んだ理論を現実の回路に結びつけるという意味で有益です。また、実際の設計において、様々な補償回路を使用する際に役立つはずです。なお、LTspiceは補償回路の設計と理解に役立ちますが、スイッチング電源の設計についてはLTpowerCADが適切なツールになります16。電源を設計する際には、LTpowerCADが補償回路を構築するための強力(で最適)な手段になることを覚えておいてください。