低コストのマイクロコントローラによる高性能な演算
要約
近年のマイクロコントローラ(µC)には、従来のALUコアに加えて、DSPと同様の機能が搭載されることがますます多くなっています。残念ながら、多くのファームウェア開発者はDSPのアルゴリズムやコーディング手法には不慣れであり、これらのデバイスに用意された機能を十分に活用することができていません。この記事は、低コストのµCにおいて、信号処理手法を使用するためのファームウェア開発者用の手引書です。
マイクロコントローラの役割の変化
µCを用いて設計するということは、CPUを取り囲む多くの周辺/サポートチップそのものを取り扱うということと等しくなっていますが、これはそれほど昔のことではありません。十分なROMやRAMがCPUに内蔵されていたとしても、重要なプロジェクトであれば、外部のサポートチップによって提供される機能が必要になると考えられます。これは、システムが何らかの種類のアナログ信号を必要とするときに最も当てはまります。アナログ信号の要件が極めて単純なものであっても、これを取り入れると、システムの複雑さは急増します。しかし、これは問題です。というのは、実世界における音、温度、気圧、およびその他の自然現象は、いつでもアナログだからです。実際、アナログの世界でシステムが動作するためには、以下が必要となります。
- 物理現象を電気信号に変換するトランスデューサとアナログ信号コンディショナ
- 少なくとも、精度と速度が十分なアナログ-ディジタルコンバータ(ADC)とディジタル-アナログコンバータ(DAC)で構成されたデータ収集サブシステム
- サンプリングデータの処理が可能なディジタルシグナルプロセッサ(DSP)
- DSP、データ収集サブシステム、およびその他周辺機器を管理するのに十分なスループットを備え、さらに制御とユーザインタフェースの機能をスムーズに実行するための帯域幅が十分に残されているµC (プログラムROMやデータRAMがµCに含まれることもあります)
このような複雑なデバイスがあるため、最終製品のコストが上昇し、ローエンドのアプリケーションの価格範囲から外れてしまいます。しかし、近年、新たな種類のµCが登場し、高性能のデータ収集サブシステム、DSPと同様の機能、およびRISC CPUコアを同じダイに統合することによって、アナログ世界とのインタフェース接続が容易になっています。最新のµCで統合可能な例を図1に示しています。
新世代のµCの1つの例がMAXQ3120です。UART、タイマ、およびI/Oポートの通常のアレイに加えて、MAXQ3120には、以下に示すアナログのインタフェース接続を容易にする一連の周辺デバイスが統合されています。
- 16ビットで1サイクル実行のRISCコア
- 1組の16ビットのシグマデルタADC
- PWMモードで動作可能な16ビットタイマ
- 40ビットのアキュムレータを備えた16 × 16乗算器
最新のµCは、アナログ周辺機器やMACなど、必要なシステム機能の大部分をデバイス内に統合しています。

図1. 従来の組み込みシステムでは、外部I/Oデバイスを接続するために、アドレスバスとデータバスを外部に取り出して、システムを完成させる必要があります。
問題についての考え方
信号処理に伴う問題は、以下の3つのステップで取り組むのが最適です。
- 何をしたいのか?問題を慎重に分析し、できるだけ小さな機能単位に問題を分割します。問題の中には、フィルタリング、信号識別、または特定タイプの信号の生成が含まれていますか?問題をより単純な一連のサブタスクに分割したら、次のステップに進む準備が完了です。
- 問題をどのように処理するのか?ここでは、文献、Web、またはその他のリソースを検索して、各タスクに関連するアルゴリズムを見つけます。これによって、概念的な問題のほとんどは、すでに解決されることがわかるでしょう。次に実行すべきは、最後のステップです。
- アルゴリズムをコーディングします。アルゴリズムをコードに変換するタスクはよく知られたタスクですが、利用可能なハードウェアリソースによって、これまで以上にこのタスクは容易になります。
以下の例では、3つのステップに忠実にしたがっています。つまり、問題を記述し、アルゴリズムと手法を提示し、最後にコード例を示して問題を解決しています。
電力の監視と測定の例
よくあるアナログとµCとのインタフェース接続の例は、AC回路の電圧と電流を測定し、負荷によって消費される電力を求めるというものです。当初、これは比較的簡単であると思われます。電圧と電流の波形が正弦波であれば、RMS電圧とRMS電流は、ピーク電圧またはピーク電流のちょうど1/ 2倍になります。RMS電圧とRMS電流を乗算し、その結果が電力(ワット単位)になります。これ以上に簡単なことはありますか?
2倍になります。RMS電圧とRMS電流を乗算し、その結果が電力(ワット単位)になります。これ以上に簡単なことはありますか?
この分析には、2つの問題があります。1番目の問題は、ほとんどの場合、電力会社から供給される電圧はほぼ正弦波ですが、電流波形は正弦波ではありません。ランプ調光器、スイッチング電源、および蛍光灯の電力線には、非正弦波の電流特性が見られます。単に定数を乗算するだけでは、RMS電流値は得られなくなります。2番目は、たとえ電流波形が正弦波であっても、電圧と電流の波形が正確に同相でなければ、RMS値を単純に乗算しても、実際の電力使用量(ワット単位)にはなりません。一般に実世界の負荷には、容量性リアクタンスや、または誘導性リアクタンス(こちらの方が多い)のいずれかが含まれています。このため、無効電力を考慮する必要があります。より良好な方法を見つけるには、基本に立ち戻る必要があります。
各瞬間における瞬間電圧と瞬間電流の積が瞬間電力です。図2は、この瞬間電力の増減する様子を図示していますが、電流の流れによっては、サイクルの一部がゼロ未満に一時的に低下する場合さえあります。合計有効電力は、単純に瞬間電圧と瞬間電流の積の時間平均になります。有効電力を求めるのは簡単です。電圧サンプルと電流サンプルを乗算して、アキュムレータに結果を加算します。十分な数のサンプルが積算されれば、その合計をサンプル数で除算するだけで、電力(ワット単位)が得られます。これをエネルギ(ワット秒単位)に変換するには、サンプルが積算された時間(秒単位)を乗算します。

図2. ほとんどの場合、電圧波形(破線)はほぼ正弦波ですが、電流波形(実線)は純粋な正弦波と大きく異なる場合があります。さらに、電流波形の位相がずれる可能性があるため、電源サイクルの特定の部分における瞬間電力(点線)はマイナスになります。
無効電力の計算は簡単ではありません。最初に、正弦波電圧と正弦波電流の場合の無効電力は、以下のように定義されます:
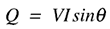
ここで、VはRMS電圧、IはRMS電流、 は電流波形と電圧波形の間の位相差です。
は電流波形と電圧波形の間の位相差です。
無効分による電力は、以下に示すように、差異を計算することでいつでも求めることができます。

および
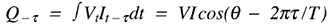
ここで、VtとItは、任意の時刻における電圧と電流の瞬間値です。また、 は任意の遅延時間、Tは電源サイクルの1周期です。差異は、次のようになります:
は任意の遅延時間、Tは電源サイクルの1周期です。差異は、次のようになります:
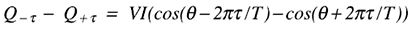
三角関数の恒等式cos(A + B) = cosAcosB - sinAsinB、およびcos(A - B) = cosAcosB + sinAsinBを使用すると、式は次のようになります:

コサインの項は相殺され、サインの項だけが強め合って残るため、式は次のようになります:
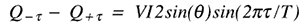
しかし、VI sin( )がQであり、これが求めようとしている値です。したがって、項を並べ替えると、次のようになります:
)がQであり、これが求めようとしている値です。したがって、項を並べ替えると、次のようになります:

この式でわかるように、無効電力は、最新の電流サンプルと前の電圧サンプルとの積と、最新の電圧サンプルと前の電流サンプルとの積の間の差を積算することによって計算することができます。 をサンプル周期に設定した場合、上式の分母は定数となり、無効電力を事前に計算することができます。
をサンプル周期に設定した場合、上式の分母は定数となり、無効電力を事前に計算することができます。
有効電力と無効電力が求まると、皮相電力(RMS電圧とRMS電力を乗算した場合に計算される電力)は、以下に示すように容易に計算することができます:
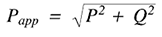
最後に、有効電力を皮相電力で除算することによって力率が求まります。
当分の間、これらすべての因子の追跡が望ましいと仮定すると、アプリケーションは、電圧チャネルと電流チャネルの積の合計、および無効電力に関して以前に説明した積の差の合計を常に把握する必要があります。有効電力を積算するためのコードは、次のようになります。
void accumulateRealPower(int i_sample, int
v_sample)
{
static long real_power;
initMAC(MULTIPLY_ADD);
preloadMAC(real_power);
real_power = getMAC(v_sample,
i_sample);
}
この例では、initMAC関数は、MACに演算パラメータを設定するための1バイトを使用します。preloadMAC関数は、乗算演算を行う前に、アキュムレータにロング変数をロードします。
これが実際のマシン命令にどのように変換されるのかを示すため、上記のコードに基づいて、以下の一連の演算を調べてみます。
- 乗加算ユニットすなわちMACを初期化します(1サイクル)。
- ストレージエリアを合計するためのメモリポインタを設定します(1サイクル)。
- 古い合計をアキュムレータにロードします(2サイクル)。
- 乗算器に電圧サンプルをロードします(1サイクル)。
- 乗算器に電流サンプルをロードします(1サイクル)。
- 積算演算が完了するまで1サイクル待ちます(1サイクル)。
- アキュムレータをメモリに保存します(1サイクル)。
このように、有効電力を積算するには8サイクルが必要です。以下に示すように、無効電力の積算もよく似ています:
void accumulateReactivePower(int i_sample, int
v_sample)
{
static long reactive_power;
initMAC(MULTIPLY_ADD);
preloadMAC(reactive_power);
reactive_power = getMAC(prev_v_sample,
i_sample);
initMAC(MULTIPLY_SUB);
reactive_power = getMAC(prev_i_sample,
v_sample);
}
この説明では、入力サンプルのDCオフセットがゼロであることを前提にしています。ゼロでない場合、電圧チャネルと電流チャネル用にそれぞれ追加のアキュムレータを用意する必要があります。DCオフセットがゼロであれば、アキュムレータの合計はゼロになります。ゼロでなければ、DCオフセットで表される電力を積算された有効電力から減算する必要があります。
フィルタリングの例
フィルタリングは、ディジタルの世界で最もよく行われる作業のひとつです。この理由は簡単です。アナログの世界では実現不能な理想的フィルタも、ディジタルロジックでは比較的簡単に実現することができるからです。
この項では、ローパスフィルタとバンドパスフィルタを紹介します。ローパスフィルタは一般的に、エイリアシングアーティファクトを除去することを目的として、サンプリングする前の信号から不要な高周波数成分を取り除くために使用します。バンドパスフィルタは、ほとんどの場合、特定の周波数範囲に通信チャネルを制限するために使用します。たとえば、FSKモデムはバンドパスフィルタを使用することで、処理対象の周波数だけを残して、高周波と低周波の両方のノイズ成分を取り除いています。
ディジタルフィルタのトピックに関して記載された書物を見れば、ディジタルフィルタを理解することは難しいと感じることでしょう。実際には、基本は簡単であり、フィルタリング機能を利用するのにDSPの専門家である必要はありません。
図3のローパスフィルタのダイアグラムを調べると、以下がわかります:
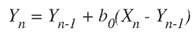
ここで、Ynは現在の出力サンプルであり、Yn-1は前の出力サンプルです。また、Xnは現在の入力サンプルです。フィルタ定数b0は、事前に計算されて、次のようになります:
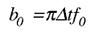
ここで、f0は所望の半振幅コーナー周波数であり、
 はサンプル周期です。したがって、サンプルレートが8kHzで所望のコーナー周波数が100Hzの場合、b0は、p × 125µs × 100Hz = 3.93 × 10-2に等しくなります。
はサンプル周期です。したがって、サンプルレートが8kHzで所望のコーナー周波数が100Hzの場合、b0は、p × 125µs × 100Hz = 3.93 × 10-2に等しくなります。
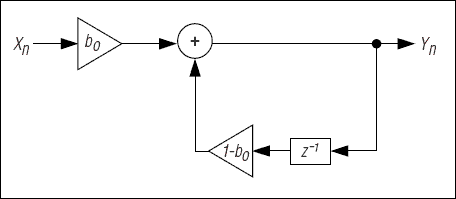
図3. 信号を送出する前に単極のローパスフィルタを使用して、信号から不要な高周波数成分を取り除きます。
以下に示すように、フィルタアルゴリズムの実装は極めて簡単です:
long lpf(int input_sample)
{
static long prev_out;
initMAC(MULTIPLY_SUB);
preloadMAC(prev_out);
prev_out = getMAC(b0, prev_out);
initMAC(MULTIPLY_ADD | ONE_OP);
prev_out = oneopMAC(input_sample);
return prev_out;
}
oneopMAC関数は、1つのオペランドのみを乗算器にロードし、乗算器が2番目のオペランドを維持することを想定しています。これは、実行時間を節約するために実施されます。このフィルタは、効率的にコンパイルすれば、1サンプル当り10サイクルしか必要としません。つまり、8MHzクロックの場合、1次ローパスフィルタはMAXQ3120の処理帯域幅の約1%しか消費しないということです(割込みのオーバヘッドは考慮していません)。
2次バンドパスフィルタは、概念上は少し複雑ですが、実際にはほぼ同様であり、アルゴリズムに数ステップを追加するだけです。簡単な2次バンドパスフィルタの信号フロー図を図4に示します。この式は、次のようになります:


図4. 2次バンドパスフィルタは、特定の周波数範囲に通信チャネルを制限することができます。
前の例と同様、パラメータのb0、a1、およびa2は、事前に計算されます。a1パラメータは、フィルタのQ値を定義しています。これは、フィルタが中心周波数近くの帯域外周波数をどの程度効果的に排除できるかの目安になります。具体的には、次のようになります。
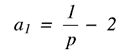
pは、一般的に100~1000の範囲です。pの値を大きくすると通過域は狭くなりますが、フィルタの整定時間は長くなります。また、pの値を小さくすると通過域は広くなり、整定時間は速くなります。
その他のパラメータa2とb0は、a1によって計算されます。最初に、以下の2つの中間変数を定義します:
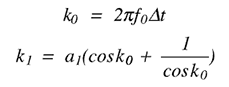
これで、以下に示すように、他の2つのパラメータを定義することができます:
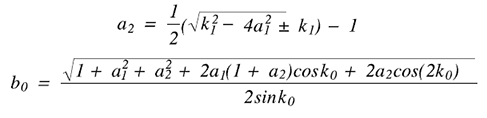
いったん中心周波数、サンプリングレート、およびフィルタのQ値を選択すれば、パラメータは定数となることに留意してください。必要なコードを以下に示します:
long bpf(int input_sample)
{
static long x[1], y[1], output;
initMAC(MULTIPLY_ADD | CLEAR_ACC);
output = getMAC(y[1], a2);
initMAC(MULTIPLY_SUB);
}
output = getMAC(y[0], a1);
output = getMAC(x[1], b0);
initMAC(MULTIPLY_ADD | ONE_OP);
output = oneopMAC(input_sample);
x[1] = x[0];
x[0] = input_sample;
y[1] = y[0];
y[0] = output;
return output;
}
効率的にコンパイルすれば、このルーチンは14サイクルを必要とします(入力サンプルと出力サンプルのエージング時間は除く)。エージング時間は、サイクルの見積もりには含まれていません。ほとんどの場合、サンプルは循環バッファに格納されるため、エージングを必要としないからです。
トーンの生成と検出の例
通信アプリケーションでは、多くの場合、オーディオチャネルでトーンの組み合わせを生成/検出することが必要となります。たとえば、電話アプリケーションでは、通常、電話回線でダイアルを回す場合、デュアルトーン多重周波数(DTMF)トーンの合成または検出が電話回線で必要となります。トランクカードでは、帯域内の信号送出に標準の多重周波数(MF)トーンがよく使用されています。呼び出し経過信号の送出(特にダイアルトーン、リングバックトーン、ビジートーン、およびリオーダートーンなど)は、たいてい2つ以上のトーンの組み合わせとして提示されます。
2極のディジタル共振器(図5)は、トーンを生成する簡単な方法です。共振器の式を以下に示します。
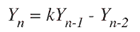
ここで、kは、
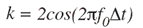
であり、事前に計算することができます。この共振器への入力がないことに留意してください。共振器は介入なしに連続して動作します。ただし、共振器を始動するには、Yn-1をゼロに設定し、Yn-2を-Asinkに設定する必要があります。ここで、Aは所望の信号振幅です。
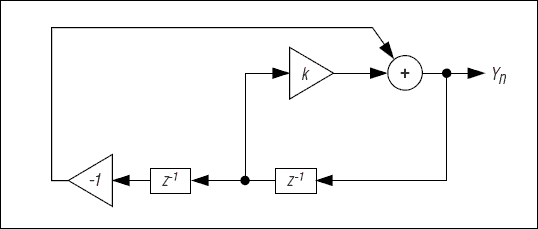
図5. 2極ディジタル共振器を使用して正弦波を生成します。
以下の正弦波を生成するアルゴリズムは、これまでの中でも最も簡単です;
long gen_tone_sample()
{
static long y[1];
initMAC(MULTIPLY_ADD);
preloadMAC(-y[1]);
y[1] = y[0];
y[0] = getMAC(y[0], k);
return y[0];
}
このルーチンのコードサイズの見積もりは、生成される正弦波のサンプル当り約8マシンサイクルです。この時のCPU使用率は、単純な方形波を生成する場合と同じ程度です。次に、正弦波は、多くのアプリケーションで必要となるスペクトル純度を生成するために外部のアナログ回路によってフィルタリングする必要があります。
トーンの検出は多少複雑ですが、必要最低限に限れば、怖れるほど困難な作業ではありません。オーディオチャネルのトーンを検出するには、Goertzelアルゴリズムを選択します。このアルゴリズムは、2次フィルタと電力測定の式を利用して、フィルタ通過域でのエネルギの有無を判断します。
図6の2次フィルタの式を以下に示します:
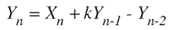
ここで、kは、前述のトーンジェネレータと同じものが定義されています。アルゴリズムを以下に示します:
long *tone_filter(int input_sample)
{
static long y[1], output;
initMAC(MULTIPLY_ADD);
preloadMAC(-y[1]);
y[1] = y[0];
y[0] = getMAC(y[0], k) +
input_sample;
return y;
}
このルーチンは、スカラ値ではなく配列を返すことに留意してください。これは、次のステップが最新の結果と前の結果の両方を必要とするからです。トーンディテクタの1つのチャネルのためのサイクルカウントの見積もりは12サイクルであり、8kHzのサンプリングレートで約1.5%のCPU能力になります。一般にフィルタが整定されてトーンの存在を確実に示せるようになるまで、100を超えるサンプル周期が必要となります。

図6. トーン検出は、2次フィルタによって行うことができます。
トーンの存在がないかテストするには、フィルタリングされた信号の電力を計算することが必要となります。これは、以下の式を使用して行うことができます:
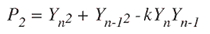
係数2cos(k)は、フィルタループ用に事前に計算した値と同じであるため、ここでこの値を使用することで、以下に示すように電力を計算することができます。
power_squared = y[0] * y[0] +
y[1] * y[1] -
k * y[0] * y[1];
十分な数のサンプル周期の後、トーンの存在は、トーンがない場合の測定値よりも少なくとも1桁大きな2乗電力の表示で示されます。テストでは、トーンの存在は、入力端でのユニティの信号振幅に対して、1,000を超える2乗振幅を示す場合があります。1つのオフ周波数のトーンまたは複数のオフ周波数のトーンの組み合わせは、通常、50未満の2乗振幅を示します。
結論
データ収集ハードウェアおよびDSPと同様の構成要素が安価なµCでますます普及するにつれ、ファームウェア技術者はコストの削減や性能の向上のため、DSPの機能をメインCPUに組み入れる方法を見つける必要があります。ただし、文献やWebで豊富なリソースが利用可能であり、この作業は予想以上に簡単です。




















