要約
There are two fundamentally different authentication schemes: symmetric systems, which rely on secret keys shared by host and authenticator, and asymmetric systems, such as the Elliptic Curve Digital Signature Algorithm (ECDSA), which rely on a private key in the authenticator and a public key that the host uses to verify the authenticator. In open systems where third-party entities need to be authenticated, the management and protection of the secret keys can be a problem. Here is where ECDSA offers the required flexibility. This article introduces the ECDSA concept, its mathematical background, and shows how the method can be successfully deployed in practice.
A similar version of this article appeared on Electronic Products May 16, 2014.
Introduction
Manufacturers of nearly all equipment types need to protect their products against the counterfeit components that aftermarket companies will attempt to introduce into the OEM supply chain. Secure authentication provides a strong electronic solution to address this threat.
Traditionally, authentication systems relied on symmetric algorithms such as secure hash algorithms[1] that require secret keys. The management and protection of the secret keys, however, can be challenging. A welcome alternative to this logistics problem is elliptic curve cryptography (ECC), where all participating devices have a pair of keys called “private key” and “public key.” The private key is used by the originator to sign a message, and the recipient uses the originator’s public key to verify the authenticity of the signature. If a message is modified on its way to the recipient, the signature verification fails because the original signature is not valid for the modified message. The Digital Signature Standard (DSS), issued by the National Institute of Standards and Technology (NIST), specifies suitable elliptic curves, the computation of key pairs, and digital signatures.[2] This article discusses the concept of the Elliptic Curve Digital Signature Algorithm (ECDSA) and shows how the method can be used in practice.
Elliptic Curves
Many readers may associate the term “elliptic” with conic sections from distant school days. An ellipsis is a special case of the general second-degree equation ax² + bxy + cy² + dx + ey + f = 0. Depending on the values of the parameters a to f, the resulting graph could be a circle, hyperbola, or parabola. Elliptic curve cryptography uses third-degree equations.
The DSS defines two kinds of elliptic curves for use with ECC: pseudo-random curves, whose coefficients are generated from the output of a seeded cryptographic hash function; and special curves, whose coefficients and underlying field have been selected to optimize the efficiency of the elliptic curve operations. Pseudo-random curves can be defined over prime fields GF(p) as well as binary fields GF(2m).
A prime field is the field GF(p), which contains a prime number p of elements. The elements of this field are the integers modulo p; the field arithmetic is implemented in terms of the arithmetic of integers modulo p. The applicable elliptic curve has the form y² = x³ + ax + b. Figure 1 shows an example of an elliptic curve in the real domain and over a prime field modulo 23. A common characteristic is the vertical symmetry.

Figure 1. Third-degree elliptic curves, real domain (left), over prime field (right).
A binary field is the field GF(2m), which contains 2m elements for some m (called the degree of the field). The elements of this field are the bit strings of length m; the field arithmetic is implemented in terms of operations on the bits. The applicable elliptic curve has the form y² + xy = x³ + ax² + b.
Although there is a virtually unlimited number of possible curves that meet the equation, only a small number of curves is relevant for ECC. These curves are referenced as NIST Recommended Elliptic Curves in FIPS publication 186. Each curve is defined by its name and domain parameters set, which consists of the Prime Modulus p, the Prime Order n, the Coefficient a, the Coefficient b, and the x and y coordinates of the Base Point G(x,y) on the curve. Table 1, for example, shows the domain parameters of curve P-192, which is a pseudo-random curve over a prime field. For more examples, see Reference 2. The numeric portion of the curve’s name indicates the length of the private key in bits. The size of public key and the digital signature is twice the length of the private key.
| Parameter Name | Notation | Value |
| Prime Modulus p |
Decimal | 6277101735386680763835789423207666416083908700390324961279 |
| Hex | FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFFFF FFFFFFFF | |
| Prime Order n |
Decimal | 6277101735386680763835789423176059013767194773182842284081 |
| Hex | FFFFFFFF FFFFFFFF FFFFFFFF 99DEF836 146BC9B1 B4D22831 | |
| Coefficient a |
Decimal | -3 (same as p - 3) |
| Hex | FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFFFF FFFFFFFC | |
| Coefficient b |
Hex | 64210519 E59C80E7 0FA7E9AB 72243049 FEB8DEEC C146B9B1 |
| x coordinate of Base Point G(x,y) |
Hex | 188DA80E B03090F6 7CBF20EB 43A18800 F4FF0AFD 82FF1012 |
| y coordinate of Base Point G(x,y) |
Hex | 07192B95 FFC8DA78 631011ED 6B24CDD5 73F977A1 1E794811 |
Mathematical Background
Elliptic curve cryptography involves scalars and points. Typically, scalars are represented with lower-case letters, while points are represented as upper-case letters, as in Table 1. Three numerical operations are defined for scalars: addition (+), multiplication (*) and inversion (-1). There are two numerical operations for points: addition (+) and multiplication (×). Although the symbol “+” is used for scalars and points, a point addition follows different rules than the scalar addition. These operations apply to curves over prime fields, as well as curves over binary fields. Algebraic formulae to perform these computations are found in Reference 3.
Computations needed for ECDSA authentication are the generation of a key pair (private key, public key), the computation of a signature, and the verification of a signature. The corresponding equations are found in public literature.[2], [3], [4] Unfortunately, different authors use their own conventions, which makes it difficult to follow their explanations. To bridge this gap, the equations are included here, strictly adhering to the conventions above.
Key Pair Generation
Before an ECDSA authenticator can function, it needs to know its private key. The public key is derived from the private key and the domain parameters. The key pair must reside in the authenticator’s memory. As the name implies, the private key is not accessible from the outside world. The public key, in contrast, must be openly read accessible. Figure 2 illustrates the generation of the key pair.

Figure 2. Key pair generation process.
A random number generator is started and, when its operation is completed, delivers the numeric value that becomes the private key d (a scalar). Next, the public key Q(x,y) is computed according to Equation 1 through point multiplication:
Q(x, y) = d × G(x, y)
Signature Computation
A digital signature allows the recipient of a message to verify the message’s authenticity using the authenticator’s public key. First, the variable-length message is converted to a fixed-length message digest h(m) using a secure hash algorithm.[1] A secure hash has the following distinctive properties: 1) irreversibility—it is computationally infeasible to determine the message from its digest; 2) collision resistance—it is impractical to find more than one message that produces a given digest; and 3) high avalanche effect—any change in the message produces a significant change in the digest. After the message digest is computed, a random number generator is activated to provide a value k for the elliptic curve computations. Figure 3 illustrates the process.

Figure 3. Signature computation process.
The signature consists of two integer numbers, r and s. Equation 2 shows the computation of r from the random number k and the base point G(x,y):
(x1, y1) = k × G(x, y) mod p
r = x1 mod n
To be valid, r must be different from zero. In the rare case when r is 0, a new random number, k, must be generated and r needs to be computed again.
After r is successfully computed, s is computed according to Equation 3 using scalar operations. Inputs are the message digest h(m); the private key d; r; and the random number k:
s = (k-1 (h(m) + d * r) mod n
To be valid, s must be different from zero. If s is 0, a new random number k must be generated and both r and s need to be computed again.
Signature Verification
The signature verification is the counterpart of the signature computation. Its purpose is to verify the message’s authenticity using the authenticator’s public key. Using the same secure hash algorithm as in the signature step, the message digest signed by the authenticator is computed which, together with the public key Q(x,y) and the digital signature components r and s, leads to the result. Figure 4 illustrates the process.
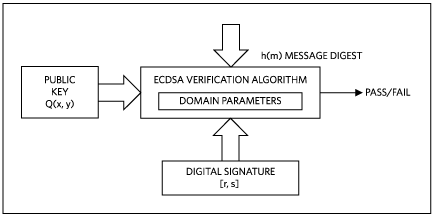
Figure 4. Signature verification process.
Equation 4 shows the individual steps of the verification process. Inputs are the message digest h(m), the public key Q(x,y), the signature components r and s, and the base point G(x,y):
w = s-1 mod n
u1 = (h(m) * w) mod n
u2 = (r * w) mod n
(x2, y2) = (u1 × G(x, y) + u2 × Q(x, y)) mod n
The verification is successful (“passes”), if x2 is equal to r, thus confirming that the signature was indeed computed using the private key.
Hardware Configuration
Implementing a secure authentication system requires linking a host system with a peripheral module (Figure 5). The host controller communicates with the authenticator over a serial bus. Any bus type could be chosen. The single pin of the 1-Wire® interface plus ground reference (no clock, no VCC) is particularly attractive since it minimizes interconnect complexity, simplifies designs, and thus reduces cost. New in Figure 5 are the System Public Key and the System Constant on the host side, and the Device ID# and the Public Key Certificate on the peripheral side.

Figure 5. Hardware configuration of an ECDSA authentication system.
Authenticator Setup
Before an authenticator can be used in an application, it must be set up. The first step is the computation and installation of a key pair (see Figure 2). The key pair can be computed externally and then be written to the authenticator. Alternatively, the authenticator may include a function block that performs this step upon external command. To prevent unauthorized changes, the key pair must be write protected.
An application can choose between two usage scenarios. In scenario 1 all authenticators are programmed with the same key pair. In this case, all hosts in the system know the valid public key. Any authenticator with that public key is considered a member of the application. No further means are needed to verify the authenticator itself.
In scenario 2 each authenticator has its own unique key pair. In this case, successful signature verification does not provide evidence that a specific authenticator device is also a member of a particular application, i.e., the “system.” Linking an authenticator to a system requires the introduction of a certificate, which is computed like a signature from the authenticator’s public key, the authenticator’s unique device ID#, a system constant, and the system private key. Figure 6 shows the computation of the certificate, as it could be performed by a key-management system, also known as “certification authority.” The two components of the certificate, cr and cs, are then stored in the authenticator’s memory and write protected. This concludes the authenticator setup. Note that in scenario 2 the host system must know both the system public key and the system constant to verify the validity of the authenticator’s public key in the application.

Figure 6. Certificate generation by a key-management system.
The infrastructure supporting the management of certificates is called a Public Key Infrastructure. Through such an infrastructure one can generate certificates and provide means for their verification. Another benefit of such infrastructure is the ability to support goods manufactured by third parties or subcontractors. Assuming that a subcontractor has manufactured goods with embedded ECDSA authenticators and that each authenticator has its own statistically unique key pair, then signing their public key to generate the certificate makes them join the system.
Authentication of a Deployed Peripheral
Figure 7 shows the typical sequence of steps. First, the authenticator is powered up (Steps 1, 2). Then the host obtains the authenticator’s Device ID#, and reads the public key and the certificate (Steps 3 to 7). Now the host performs the signature verification algorithm for the certificate (Step 8, Figure 8). If the result is “pass,” the public key is valid in the system. If the result is “fail,” the authenticator does not belong to the system; the host can skip Steps 9 to 12 and immediately deactivate the authenticator (Steps 13–15).

Figure 7. Typical transaction flow to authenticate a deployed peripheral.

Figure 8. Verifying the authenticator’s public key using the certificate.
Knowing that an authenticator’s public key is valid in the system does not guarantee that the host is communicating with a genuine authenticator. The data used so far could also have come from an emulator that tries to perform a replay attack.
To determine whether the authenticator in the peripheral is genuine, the host reads one of the authenticator’s memory pages (Step 9), sends a random challenge to the authenticator (Step 10), and instructs it to compute a signature. The message consists of the memory page data, the challenge, the device ID#, page # plus padding and formatting. Figure 9 shows how an ECDSA authenticator computes a signature. The signature is computed in real time using the authenticator’s hardware ECDSA engine. The signature’s two components r and s are sent to the host (Step 11) for verification. Note that the signature computation involves the authenticator’s private key and a random number. Consequently, even if the challenge stays the same, subsequent signature computations deliver different signature values.

Figure 9. Signature computation performed by the authenticator.

Figure 10. Verifying the signature computed by the authenticator.
Now with all the necessary data including the signature, the host computes the message digest and performs the signature verification algorithm for the signature (Step 12, Figure 10). If the result is “pass,” the authenticator is verified as genuine. If the result is “fail,” the key pair in the authenticator is not valid and the host rejects the peripheral.
Affordable Elliptic-Curve Public-Key Authentication Security
The Digital Signature Standard was originally released in 1994 and for a long time ECDSA authentication was mostly a subject of theoretical research. This situation changed recently with products such as the Maxim DeepCover® Secure Authenticator DS28E35, the first ECDSA authenticator with 1-Wire interface and 1Kbit user EEPROM. DeepCover-embedded security solutions cloak sensitive data under multiple layers of advanced physical security to provide the most secure key storage possible.
The DS28E35 implements ECC using a pseudo-random curve over a prime field according to equation y² = x³ + ax + b using the domain parameters of curve P-192 (Table 1). The device can compute, install, and lock the private/public key pair on its own; it does not need any outside help. Separate memory space is set aside to store and lock a public-key certificate. The DS28E35 also features a one-time-settable, nonvolatile, 17-bit decrement-on-command counter. This counter can be used to track the lifetime of the peripheral in which the DS28E35 is embedded. Each device has its own guaranteed unique 64-bit device ID# factory programmed into the chip. As shown above, the device ID# is a fundamental input parameter for cryptographic operations. The simplicity of the 1-Wire interface (using only I/O and GND in Figure 5) facilitates the use of the DS28E35 in a broad array of applications. As a value-added service option, device setup (key pair, certificate) including user-memory programming and counter initialization can be performed by Maxim’s secure factory personalization service. This service is a secure method for configuring parts prior to shipment into the OEM supply chain. It thus eliminates the possibility of exposure of sensitive data and offloads the necessary key management systems and efforts.
Summary
The main benefit of ECDSA is that the party authenticating the peripheral is relieved from the constraint to securely store a secret. The authenticating party can authenticate thanks to a public key that can be freely distributed. Authentication ICs, such as those among Maxim's DeepCover embedded security solutions, help simplify implementation of robust challenge-response authentication methods that form the foundation of more effective application security. The ECDSA authenticators also enable easier authentication of goods from third parties or subcontractors.




















