アナログ・ダイアログの2017年12月号から、アクティブ・ラーニング・モジュール「ADALM1000」について紹介しています。その第8回目となる今回も、引き続き同モジュールを使用して、小規模かつ基本的な測定を行う方法を説明します。ADALM1000に関する以前の記事は、こちらからご覧になれます。
目的
今回は、LC並列共振回路で生じる発振の観測を行います。その上で、現実のインダクタで生じる自己共振も観測してみます。
背景
共振回路は、同調回路とも呼ばれます。インダクタとコンデンサを組み合わせて、電圧源または電流源に接続することで実現されます。共振回路は、電子機器で使われる非常に重要な回路の1つです。数多くの種類と用途がありますが、代表的なものとしては、ラジオ局やテレビ局の選局に使われる共振回路が挙げられます。常に周囲に存在する膨大な数の信号の中から、所望のラジオ局やテレビ局を選局することができるのは、その共振回路のおかげです。
共振回路は、その入力端子の電圧と電流が同相で、入力インピーダンスが抵抗成分のみである場合に共振状態になります。
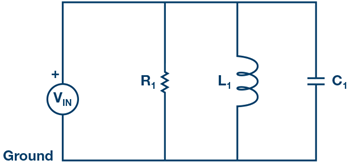
ここでは、図2に示したRLC並列回路を例にとります。この回路によって与えられる定常状態のアドミタンスは、次式のようになります。
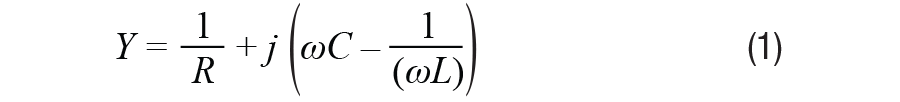
上述したように、共振は、入力端子の電圧と電流が同相のときに発生します。この状況は、アドミタンスが実数である場合に生じます。そのため、必要条件は次式で与えられます。

L、C、またはωを調整することによって、共振の条件が成立します。LとCを一定にすると、共振周波数ωoは以下のようになります。

あるいは、以下のように表現することもできます。
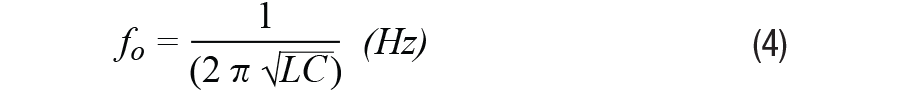
準備するもの
- ADALM1000
- ソルダーレス・ブレッドボード、ジャンパ線
- インダクタ:4.7mH(またはそれ以上)
- コンデンサ:10μF
- 抵抗:1kΩ
- 小信号用のダイオード(1N914)
説明
まず、実験用に簡単な分流回路を構成します。その回路では、ダイオードをスイッチとして使用します。
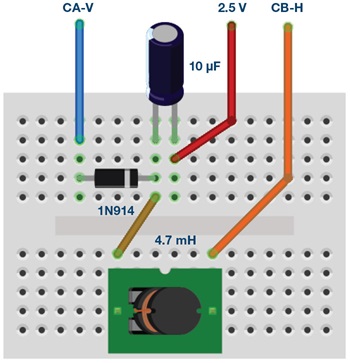
ソルダーレス・ブレッドボードを使って、図3に示す回路を構成します。そして、「AWG CH-A」からサイン波を出力するように設定を行います。サイン波の仕様は、周波数が100Hz、「Min」の値が0.5V、「Max」の値が4.5V(つまり、Vp-pが4V)とします。チャンネルAについては、サイン波の2サイクル分が表示されるように水平方向の時間スケールを調整します。「Channel B」を「Hi-Z Mode」に設定し、D1とR1をつないだ点に接続します。


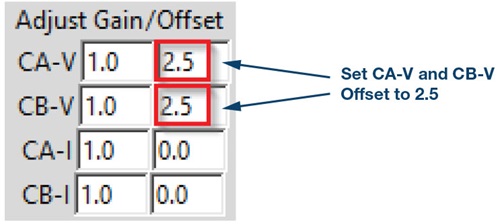
手描きの回路図を作成し、ADALM1000 からCH-A、2.5V、CH-Bへの接続に注意深くラベル付けします。ラベルに関する情報は、実験レポートに記載しておきましょう。トレースを表示するために、「Curves」ドロップダウン・メニューから「CA-V」、「CA-I」、「CB-V」を選択します。スコープ画面の右側で、「CA-V」と「CB-V」のオフセットを調節するために、2.5Vという値を入力します。この実験において、すべての測定値は2.5Vの共通レールを基準にします。また、「CH-A」と「CH-B」の垂直位置の設定値に0を入力します(スコープ画面の下部)。垂直方向の目盛は、現在、0を中心として-2.5~2.5の範囲になっているはずです。
以上の設定を終えたら、「Run」をクリックします。ここまで、詳細な説明を行ってきましたが、以下のステップでは適宜説明を省略します。この実験のいくつかのステップでは、掃引の開始/停止を行う必要がありますが、それについては把握済みであることを前提として説明を進めます。
「Math」ドロップダウン・メニューを使って、CH-AとCH-Bの違いを確認できるようにするためのトレースを追加します。この実験では、垂直方向のスケールが、表示されている3つの信号ですべて同じであることを確認します。
サイン波がダイオードを通過するときの波形と、Channel Aから供給されている電流の波形を観測します。それらの波形については、文章での説明を加えます。表示を保存し、実験レポートにコピー&ペーストしてください。AWGのソースによって生成された入力電圧、同ソースによって供給された電流、抵抗にかかる出力電圧にラベル付けします。また、重要なポイントについては、各信号の振幅を表示してみます(プロットの目盛を見るだけでは値はわかりません) 。
1. この実験におけるダイオードの役割
「AWG A」の波形を「square wave output」に切り替え、オシロスコープに数サイクル分の信号が表示されることを確認します。この波形も保存し、レポートにコピー&ペーストしておきます。すべてのプロットには注釈を付加してください。
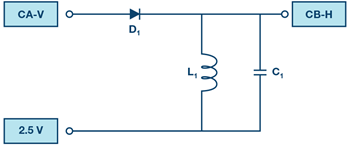
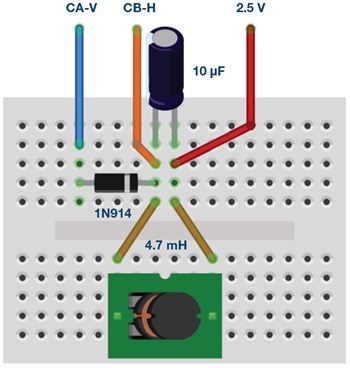
続いて、ブレッドボード上の回路を図5のように再構成します。使用する部品は、ダイオード、インダクタ、コンデンサです。ダイオードにチャンネルAを接続し、コンデンサとインダクタをつないだ点にチャンネルBを接続します。
2. 回路の発振周波数を算出する
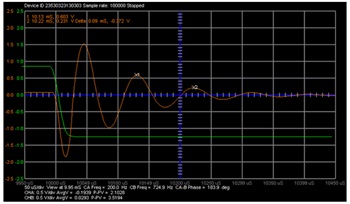
次に、オシロスコープを使って、回路が発振する周波数を測定します。100Hzの矩形波を加えたとき、LC回路は矩形波の立下がりエッジの直後に発振を開始します。グリッドの左側に発振の位置がくるように、水平方向の位置あるいはホールドオフ時間を変更します。それによって、できるだけ多くの発振波形を確認できるようにします。
発振周期を観測/測定しやすくするために、「Horizontal Time/Div」を変更します。掃引を停止した状態で(赤色の停止ボタンを使います)グリッドを左クリックすることにより、表示用のマーカー・ポイントが加わります。最後の2つのマーカーに対応する電圧および時間の差分も表示されます。発振信号のピークまたは谷のうち隣接する2点選択し、それらの間の時間差を測って周期を求めます。この表示も保存し、レポートにコピー&ペーストします(あらゆる注釈も付加しておきます)。
3. 周期の値を基に回路の発振周波数を算出する
周期の測定値を基に算出した周波数は、周波数の理論値とほぼ等しくなるはずです。そうでない場合、回路や計算に使用した各部品の値を確認してください。実測によって求めた周波数が、理論値より高いか低いかということも、レポートに記録します。
ここでダイオードを使用した理由を説明しましょう。ダイオードでは、一方向のみに電流が流れます。矩形波の振幅が2.5Vのレールよりも上にある間は、ダイオードが導通してLC共振回路にエネルギーが供給されます。2.5Vのレールよりも下にある間は、ダイオードは導通しません。その間、LC共振回路は事実上AWGのソースから切り離され、自律的に発振することになります。
4. 振幅は一定か? 増大/減衰していないか?
観測された波形と理論値に差がある理由について検討する必要があります。インダクタの仕様書を確認し、振幅の増大/減衰は、どのような特性が原因で生じるのか考察します(仕様書に記載されたすべての事柄を読むことを強くお勧めします)。
ここで、矩形波の「Min」の値を0.5V、「Max」の値を3.5V(つまり、Vp-pは3V)に変更します。
先ほどと同じ測定を繰り返し、再びプロットのデータを保存すると共に、注釈を加えます。矩形波の「Min」と「Max」の値を様々に組み合わせて、どのようなことが起きるか調べてみます。
5. プロットを比較し、電圧の差について検討する
エネルギーの蓄積
並列に接続されたコンデンサとインダクタの両端の電圧は、減衰シヌソイド(減衰正弦波)になっているはずです。現実に即したインダクタのモデルには、直列抵抗が含まれます。その抵抗に電流が流れるとき、共振部のエネルギーの一部が熱に変換されます。このエネルギー損失によって、発振の振幅は徐々に減衰します。
共振部の電圧のほか、コンデンサとインダクタの電流も測定してみます。まず、コンデンサの電流を求めるためには、次の式を使用します。

コンデンサの電圧について、離散時間の微分係数を算出します。そのためには、連続時間の信号をサンプリングした2つのサンプルの差を求め、それらのサンプル間の時間差で割ります。サンプル間の時間差というのは、サンプリング・レートの逆数です。ADALM1000では、サンプリング・レートが100kSPSなので、サンプル間の時間は10マイクロ秒です。C1の値は10μFなので、10マイクロ秒で割るとちょうど相殺されます。この式では電流の単位はAです。ここではmAを単位としてプロットするために、1000倍することにします。「Math」軸を「I-A」に設定し、「Math」の式に次式を入力します。
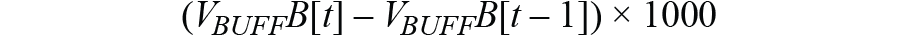
図5の回路を見ると、ダイオードがオフになり、共振部が発振しているとき、コンデンサの電流の行き先はインダクタだけであることがわかります。つまり、次式が成り立ちます。

インダクタの電流波形とコンデンサの電圧波形から、それぞれの瞬時エネルギーを算出できます。「Math」の式を使って、2つのエネルギー波形を時間の関数としてプロットします。
1つはインダクタにおけるエネルギーです。インダクタンスの単位はJ/A2です。エネルギーをJで表すと、次式のようになります。

ここでは4.7mHのインダクタを使用していますが、その値の1/2は0.00235Hです。40mAの電流が流れている4.7mHのインダクタは0.00000376J、つまりは3.76μJのエネルギーを蓄積します。値が非常に小さいので、106倍して扱うことにします。インダクタのエネルギーをμJ単位でプロットするために、「Math」の式に次式を入力します。
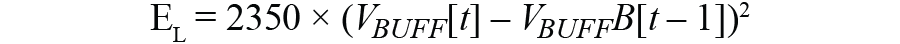
もう1つはコンデンサにおけるエネルギーです。容量の単位はC2/Jです。コンデンサに蓄積される電荷量をCを使って表すと、容量×電圧に等しくなります。したがって、エネルギーをJで表すと、次式のようになります。

ここでは10μFのコンデンサを使用しており、その容量値の1/2は0.000005Fです。1Vで充電された10μFのコンデンサは0.000005J、つまりは5μJのエネルギーを蓄えています。値が非常に小さいので、ここでも106倍して扱うことにします。コンデンサのエネルギーをμJ単位でプロットするために、「Math」の式に次式を入力します。
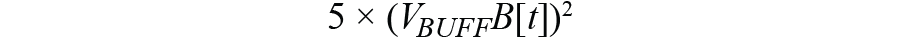
これらのプロットを保存してリポートにコピー&ペーストし、注釈を付加しておきます。
2つのエネルギーの値、2つのエネルギーの経時変化、両者の関係について検討しましょう。例えば、インダクタにエネルギーの大半、あるいはすべてが蓄積されるのはいつでしょう。また、コンデンサにエネルギーの大半、あるいはすべてが蓄積されるのはいつでしょうか。時間の経過やサイクルごとに、どのような変化が現れるでしょうか。できるだけ定量化しつつ、全体像に注目してみましょう。
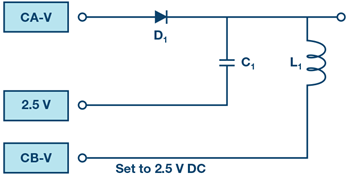
インダクタの電流は、2.5V の電源レールから切り離し、図7に示すようにAWGのチャンネルBに接続することによって直接測定することができます。その際には「AWG CH-B」を「SVMI Mode」に設定します。また、「Shape」については、「Max」の値として2.5Vを与え、dcを選択します。更に「Curves」メニューから「CB-I trace」を選択します。
算出したコンデンサの電流(および同様の推論に基づくインダクタの電流)のトレースを比較します。違いに注目し、その理由を説明してみてください。
コンデンサの電流を直接測定するためには、この測定手法をどのように使えばよいでしょうか。
自己共振
現実のインダクタには、必ず寄生容量(浮遊容量)が存在します。そのため、現実のインダクタは、並列にコンデンサが接続されているかのような挙動を示します。
ブレッドボードからコンデンサを取り除き、インダクタが発振する周波数を測定します。必要に応じて水平方向の時間スケールを調整し、発振の様子をはっきりと観測できるようにします。インダクタが自己共振する高い周波数を測定する際には、おそらく(オプション・メニューの下の)「Waveform Smoothing」をターン・オンするとよいでしょう。
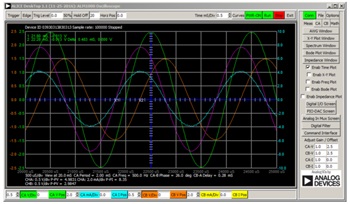
自己共振の例
図9に、自己共振の典型的な波形を示しました。この例では、4.7mHのインダクタを使用しています。
問題
- 寄生容量の値を算出してください。
- インダクタにも、モデル化するときに無視すべきではない寄生素子が他にもあります。それは、内部に存在する直列抵抗です。この抵抗によって、LC回路で測定した発振信号にはどのような影響が及んでいるのでしょうか。
付録
注記
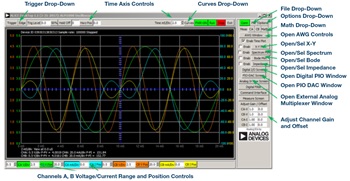
アクティブ・ラーニング・モジュールを使用する記事では、本稿と同様に、ADALM1000に対するコネクタの接続やハードウェアの設定を行う際、以下のような用語を使用することにします。まず、緑色の影が付いた長方形は、ADALM1000が備えるアナログI/Oのコネクタに対する接続を表します。アナログI /Oチャンネルのピンは「CA」または「CB」と呼びます。電圧を印加して電流の測定を行うための設定を行う場合には、「CA-V」のように「-V」を付加します。また、電流を印加して電圧を測定するための設定を行う場合には、「CA-I」のように「-I」を付加します。1つのチャンネルをハイ・インピーダンス・モードに設定して電圧の測定のみを行う場合、「CA-H」のように「-H」を付加して表します。
同様に、表示する波形についても、電圧の波形は「CA-V」と「CB-V」、電流の波形は「CA-I」と「CB-I」のように、チャンネル名とV( 電圧) 、I( 電流)を組み合わせて表します。
本稿の例では、ALICE(Active Learning Interface for Circuits and Electronics)の Rev 1.1 を使用しています。同ツールのファイル(alice-desktop-1.1-setup.zip)は、こちらからダウンロードすることができます。
ALICEは、次のような機能を提供します。
- 電圧/電流波形の時間領域での表示、解析を行うための2チャンネルのオシロスコープ
- 2チャンネルのAWG(任意信号発生器)の制御
- 電圧と電流のデータのX/Y軸プロットや電圧波形のヒストグラムの表示
- 2チャンネルのスペクトル・アナライザによる電圧信号の周波数領域での表示、解析
- スイープ・ジェネレータを内蔵したボーデ・プロッタとネットワーク・アナライザ
- インピーダンス・アナライザによる複雑なRLC回路網の解析、RLCメーター機能、ベクトル電圧計機能
- 既知の外付け抵抗、または50Ωの内部抵抗に関連する未知の抵抗の値を測定するためのDC抵抗計
- 2.5Vの高精度リファレンス「AD584」を利用して行うボードの自己キャリブレーション。同リファレンスはアナログ・パーツ・キット「ADALP2000」に含まれている
- ALICE M1Kの電圧計
- ALICE M1Kのメーター・ソース
- ALICE M1Kのデスクトップ・ツール
詳細についてはこちらをご覧ください。
注) このソフトウェアを使用するには、PC にADALM1000を接続する必要があります。