Abstract
This application note is a tutorial overview of spread-spectrum principles. The discussion covers both direct-sequence and fast-hopping methods. Theoretical equations are given to allow performance estimates. Relation to CDMA and TDMA is provided. A schematic of a code sequence generator is shown. Spectral plots illustrate direct-sequence spread-spectrum (DSSS) and frequency-hopping spread-spectrum (FHSS) methods.
Introduction
As spread-spectrum techniques become increasingly popular, electrical engineers outside the field are eager for understandable explanations of the technology. There are books and websites on the subject, but many are hard to understand or describe some aspects while ignoring others (e.g., the DSSS technique with extensive focus on PRN-code generation).
The following discussion covers the full spectrum (pun intended).
A Short History
Spread-spectrum communications technology was first described on paper by an actress and a musician! In 1941 Hollywood actress Hedy Lamarr and pianist George Antheil described a secure radio link to control torpedoes. They received U.S. Patent #2.292.387. The technology was not taken seriously at that time by the U.S. Army and was forgotten until the 1980s, when it became active. Since then the technology has become increasingly popular for applications that involve radio links in hostile environments.
Typical applications for the resulting short-range data transceivers include satellite-positioning systems (GPS), 3G mobile telecommunications, W-LAN (IEEE® 802.11a, IEEE 802.11b, IEEE 802.11g), and Bluetooth®. Spread-spectrum techniques also aid in the endless race between communication needs and radio-frequency availability—situations where the radio spectrum is limited and is, therefore, an expensive resource.
Theoretical Justification for Spread Spectrum
Spread-spectrum is apparent in the Shannon and Hartley channel-capacity theorem:
C = B × log2 (1 + S/N)
In this equation, C is the channel capacity in bits per second (bps), which is the maximum data rate for a theoretical bit-error rate (BER). B is the required channel bandwidth in Hz, and S/N is the signal-to-noise power ratio. To be more explicit, one assumes that C, which represents the amount of information allowed by the communication channel, also represents the desired performance. Bandwidth (B) is the price to be paid, because frequency is a limited resource. The S/N ratio expresses the environmental conditions or the physical characteristics (i.e., obstacles, presence of jammers, interferences, etc.).
There is an elegant interpretation of this equation, applicable for difficult environments, for example, when a low S/N ratio is caused by noise and interference. This approach says that one can maintain or even increase communication performance (high C) by allowing or injecting more bandwidth (high B), even when signal power is below the noise floor. (The equation does not forbid that condition!)
Modify Equation 1 by changing the log base from 2 to e (the Napierian number) and by noting that ln = loge. Therefore:
C/B = (1/ln2) × ln(1 + S/N) = 1.443 × ln(1 + S/N)
Applying the MacLaurin series development for
ln(1 + x) = x - x²/2 + x³/3 - x4/4 + ... + (-1)k+1xk/k + ...:
C/B = 1.443 × (S/N - 1/2 × (S/N)² + 1/3 × (S/N)³ - ...)
S/N is usually low for spread-spectrum applications. (As just mentioned, the signal power density can even be below the noise level.) Assuming a noise level such that S/N << 1, Shannon's expression becomes simply:
C/B ≈ 1.433 × S/N
Very roughly:
C/B ≈ S/N
Or:
N/S ≈ B/C
To send error-free information for a given noise-to-signal ratio in the channel, therefore, one need only perform the fundamental spread-spectrum signal-spreading operation: increase the transmitted bandwidth. That principle seems simple and evident. Nonetheless, implementation is complex, mainly because spreading the baseband (by a factor that can be several orders of magnitude) forces the electronics to act and react accordingly, which, in turn, makes the spreading and despreading operations necessary.
Definitions
Different spread-spectrum techniques are available, but all have one idea in common: the key (also called the code or sequence) attached to the communication channel. The manner of inserting this code defines precisely the spread-spectrum technique. The term "spread spectrum" refers to the expansion of signal bandwidth, by several orders of magnitude in some cases, which occurs when a key is attached to the communication channel.
The formal definition of spread spectrum is more precise: an RF communications system in which the baseband signal bandwidth is intentionally spread over a larger bandwidth by injecting a higher frequency signal (Figure 1). As a direct consequence, energy used in transmitting the signal is spread over a wider bandwidth, and appears as noise. The ratio (in dB) between the spread baseband and the original signal is called processing gain. Typical spread-spectrum processing gains run from 10dB to 60dB.
To apply a spread-spectrum technique, simply inject the corresponding spread-spectrum code somewhere in the transmitting chain before the antenna (receiver). (That injection is called the spreading operation.) The effect is to diffuse the information in a larger bandwidth. Conversely, you can remove the spread-spectrum code (called a despreading operation) at a point in the receive chain before data retrieval. A despreading operation reconstitutes the information into its original bandwidth. Obviously, the same code must be known in advance at both ends of the transmission channel. (In some circumstances, the code should be known only by those two parties.)

Figure 1. Spread-spectrum communication system.
Bandwidth Effects of the Spreading Operation
Figure 2 illustrates the evaluation of signal bandwidths in a communication link.

Figure 2. Spreading operation spreads the signal energy over a wider frequency bandwidth.
Spread-spectrum modulation is applied on top of a conventional modulation such as BPSK or direct conversion. One can demonstrate that all other signals not receiving the spread-spectrum code will remain as they are, that is, unspread.
Bandwidth Effects of the Despreading Operation
Similarly, despreading can be seen in Figure 3.

Figure 3. The despreading operation recovers the original signal.
Here a spread-spectrum demodulation has been made on top of the normal demodulation operations. One can also demonstrate that signals such as an interferer or jammer added during the transmission will be spread during the despreading operation!
Waste of Bandwidth Due to Spreading Is Offset by Multiple Users
Spreading results directly in the use of a wider frequency band by a factor that corresponds exactly to the "processing gain" mentioned earlier. Therefore spreading does not spare the limited frequency resource. That overuse is well compensated, however, by the possibility that many users will share the enlarged frequency band (Figure 4).

Figure 4. The same frequency band can be shared by multiple users with spread-spectrum techniques.
Spread Spectrum Is a Wideband Technology
In contrast to regular narrowband technology, the spread-spectrum process is a wideband technology. W-CDMA and UMTS, for example, are wideband technologies that require a relatively large frequency bandwidth, compared to narrowband radio.Benefits of Spread Spectrum
Resistance to Interference and Antijamming Effects
There are many benefits to spread-spectrum technology. Resistance to interference is the most important advantage. Intentional or unintentional interference and jamming signals are rejected because they do not contain the spread-spectrum key. Only the desired signal, which has the key, will be seen at the receiver when the despreading operation is exercised. See Figure 5.

Figure 5. A spread-spectrum communication system. Note that the interferer's energy is spread while the data signal is despread in the receive chain
You can practically ignore the interference, narrowband or wideband, if it does not include the key used in the despreading operation. That rejection also applies to other spread-spectrum signals that do not have the right key. Thus different spread-spectrum communications can be active simultaneously in the same band, such as CDMA. Note that spread spectrum is a wideband technology, but the reverse is not true: wideband techniques need not involve spread-spectrum technology.
Resistance to Interception
Resistance to interception is the second advantage provided by spread-spectrum techniques. Because nonauthorized listeners do not have the key used to spread the original signal, those listeners cannot decode it. Without the right key, the spread-spectrum signal appears as noise or as an interferer. (Scanning methods can break the code, however, if the key is short.) Even better, signal levels can be below the noise floor, because the spreading operation reduces the spectral density. See Figure 6. (Total energy is the same, but it is widely spread in frequency.) The message is thus made invisible, an effect that is particularly strong with the direct-sequence spread-spectrum (DSSS) technique. (DSSS is discussed in greater detail below.) Other receivers cannot "see" the transmission; they only register a slight increase in the overall noise level!

Figure 6. Spread-spectrum signal is buried under the noise level. The receiver cannot "see" the transmission without the right spread-spectrum keys.
Resistance to Fading (Multipath Effects)
Wireless channels often include multiple-path propagation in which the signal has more than one path from the transmitter to the receiver (Figure 7). Such multipaths can be caused by atmospheric reflection or refraction, and by reflection from the ground or from objects such as buildings.

Figure 7. Illustration of how the signal can reach the receiver over multiple paths.
The reflected path (R) can interfere with the direct path (D) in a phenomenon called fading. Because the despreading process synchronizes to signal D, signal R is rejected even though it contains the same key. Methods are available to use the reflected-path signals by despreading them and adding the extracted results to the main one.
Spread Spectrum Allows CDMA
Note that spread spectrum is not a modulation scheme, and should not be confused with other types of modulation. One can, for example, use spread-spectrum techniques to transmit a signal modulated by FSK or BPSK. Thanks to the coding basis, spread spectrum can also be used as another method for implementing multiple access (i.e., the real or apparent coexistence of multiple and simultaneous communication links on the same physical media). So far, three main methods are available.
FDMA—Frequency Division Multiple Access
FDMA allocates a specific carrier frequency to a communication channel. The number of different users is limited to the number of "slices" in the frequency spectrum (Figure 8). Of the three methods for enabling multiple access, FDMA is the least efficient in term of frequency-band usage. Methods of FDMA access include radio broadcasting, TV, AMPS, and TETRAPOLE.

Figure 8. Carrier-frequency allocations among different users in a FDMA system.
TDMA—Time Division Multiple Access
With TDMA the different users speak and listen to each other according to a defined allocation of time slots (Figure 9). Different communication channels can then be established for a unique carrier frequency. Examples of TDMA are GSM, DECT, TETRA, and IS-136.

Figure 9. Time-slot allocations among different users in a TDMA system.
CDMA—Code Division Multiple Access
CDMA access to the air is determined by a key or code (Figure 10). In that sense, spread spectrum is a CDMA access. The key must be defined and known in advance at the transmitter and receiver ends. Growing examples are IS-95 (DS), IS-98, Bluetooth, and WLAN.

Figure 10. CDMA systems access the same frequency band with unique keys or codes.
One can, of course, combine the above access methods. GSM, for instance, combines TDMA and FDMA. GSM defines the topological areas (cells) with different carrier frequencies, and sets time slots within each cell.
Spread Spectrum and (De)coding "Keys"
At this point, it is worth restating that the main characteristic of spread spectrum is the presence of a code or key, which must be known in advance by the transmitter and receiver(s). In modern communications the codes are digital sequences that must be as long and as random as possible to appear as "noise-like" as possible. But in any case, the codes must remain reproducible, or the receiver cannot extract the message that has been sent. Thus, the sequence is "nearly random." Such a code is called a pseudo-random number (PRN) or sequence. The method most frequently used to generate pseudo-random codes is based on a feedback shift register.
One example of a PRN is shown in Figure 11. The shift register contains eight data flip-flops (FF). At the rising edge of the clock, the contents of the shift register are shifted one bit to the left. The data clocked in by FF1 depends on the contents fed back from FF8 and FF7. The PRN is read out from FF8. The contents of the FFs are reset at the beginning of each sequence length.

Figure 11. Block diagram of a sample PRN generator.
Many books are available on the generation of PRNs and their characteristics, but that development is outside the scope of this basic tutorial. Simply note that the construction or selection of proper sequences, or sets of sequences, is not trivial. To guarantee efficient spread-spectrum communications, the PRN sequences must respect certain rules, such as length, autocorrelation, cross-correlation, orthogonality, and bits balancing. The more popular PRN sequences have names: Barker, M-Sequence, Gold, Hadamard-Walsh, etc. Keep in mind that a more complex sequence set provides a more robust spread-spectrum link. But there is a cost to this: more complex electronics both in speed and behavior, mainly for the spread-spectrum despreading operations. Purely digital spread-spectrum despreading chips can contain more than several million equivalent 2-input NAND gates, switching at several tens of megahertz.
Different Modulation Spreading Techniques for Spread Spectrum
Different spread-spectrum techniques are distinguished according to the point in the system at which a PRN is inserted in the communication channel. This is very basically illustrated in the RF front-end schematic in Figure 12.
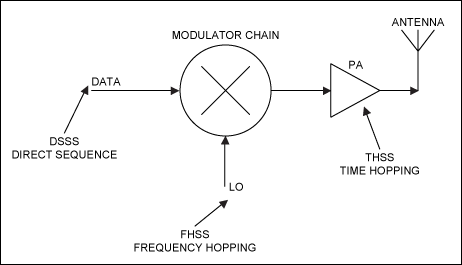
Figure 12. Several spreading techniques are applied at different stages of the transmit chain.
If the PRN is inserted at the data level, this is the direct-sequence form of spread spectrum (DSSS). (In practice, the pseudo-random sequence is mixed or multiplied with the information signal, giving an impression that the original data flow was "hashed" by the PRN.) If the PRN acts at the carrier-frequency level, this is the frequency-hopping form of spread spectrum (FHSS). Applied at the LO stage, FHSS PRN codes force the carrier to change or "hop" according to the pseudo-random sequence. If the PRN acts as an on/off gate to the transmitted signal, this is a time-hopping spread-spectrum technique (THSS). There is also the "chirp" technique, which linearly sweeps the carrier frequency in time.
One can mix all the above techniques to form a hybrid spread-spectrum technique, such as DSSS + FHSS. DSSS and FHSS are the two techniques most in use today.
Direct-Sequence Spread Spectrum (DSSS)
With the DSSS technique, the PRN is applied directly to data entering the carrier modulator. The modulator, therefore, sees a much larger bit rate, which corresponds to the chip rate of the PRN sequence. Modulating an RF carrier with such a code sequence produces a direct-sequence-modulated spread spectrum with ((sin x)/x)² frequency spectrum, centered at the carrier frequency.
The main lobe of this spectrum (null to null) has a bandwidth twice the clock rate of the modulating code, and the side lobes have null-to-null bandwidths equal to the code's clock rate. Illustrated in Figure 13 is the most common type of direct-sequence-modulated spread-spectrum signal. Direct-sequence spectra vary somewhat in spectral shape, depending on the actual carrier and data modulation used. Below is a binary phase shift keyed (BPSK) signal, which is the most common modulation type used in direct-sequence systems.

Figure 13. Spectrum-analyzer photo of a DSSS signal. Note the original signal (nonspread) would only occupy half of the central lobe.
Frequency-Hopping Spread Spectrum (FHSS)
The FHSS method does exactly what its name implies—it causes the carrier to hop from frequency to frequency over a wide band according to a sequence defined by the PRN. The speed at which the hops are executed depends on the data rate of the original information. One can, however, distinguish between fast frequency hopping (FFHSS) and low frequency hopping (LFHSS). The latter method, the most common, allows several consecutive data bits to modulate the same frequency. FFHSS is characterized by several hops within each data bit.
The transmitted spectrum of a frequency-hopping signal is quite different from that of a direct-sequence system. Instead of a ((sin x)/x)²-shaped envelope, the frequency hopper's output is flat over the band of frequencies used (see Figure 14). The bandwidth of a frequency-hopping signal is simply N times the number of frequency slots available, where N is the bandwidth of each hop channel.

Figure 14. Spectrum-analyzer photo of a FHSS signal.
Time-Hopping Spread Spectrum (THSS)

Figure 15. THSS block diagram.
Figure 15 illustrates THSS, a method not well developed today. Here the on and off sequences applied to the PA are dictated according to the PRN sequence.
Implementations and Conclusions
A complete spread-spectrum communication link requires various advanced and up-to-date technologies and disciplines: an RF antenna, a powerful and efficient PA, a low-noise and highly linear LNA, compact transceivers, high-resolution ADCs and DACs, rapid low-power digital signal processing (DSP), etc. Though designers and manufacturers compete, they are also joining in their effort to implement spread-spectrum systems.
The most difficult area is the receiver path, especially at the despreading level for DSSS, because the receiver must be able to recognize the message and synchronize with it in real time. The operation of code recognition is also called correlation. Because correlation is performed at the digital-format level, the tasks are mainly complex arithmetic calculations including fast, highly parallel, binary additions and multiplications.
The most difficult aspect of today's receiver design is synchronization. More time, effort, research, and money have gone toward developing and improving synchronization techniques than toward any other aspect of spread-spectrum communications. Several methods can solve the synchronization problem, and many of them require a large number of discrete components to implement. Perhaps the biggest breakthroughs have occurred in DSP and in application-specific integrated circuits (ASICs). DSP provides high-speed mathematical functions that analyze, synchronize, and decorrelate a spread-spectrum signal after slicing it in many small parts. ASIC chips drive down costs with VLSI technology and by the creation of generic building blocks suitable for any type of application.




