Clocking Wideband GSPS JESD204B ADCs
As high speed signal acquisition applications using multiple analog-to-digital converters (ADCs) increase in complexity, each converter’s complementary clock solution will dictate the dynamic range and capacity of the system’s potential. With the increase in sample rate and input bandwidth of emerging gigasample per second (GSPS) ADCs, the capability and performance of the system’s distributed sample clock becomes critical. System solutions that target high frequency measurements, such as electrical measurement instrumentation and multiconverter array applications, will need leading edge clocking solutions.
Focused selection of the companion clock solution is important to prevent limitation of the ADC’s dynamic range. Depending upon the input bandwidth and frequency of interest, the clock jitter can otherwise limit the performance of the ADC. Low jitter and phase noise, distribution deskew, and alignment capabilities for the converter’s high speed JESD204B serial interface are all clocking attributes that become paramount for optimum system performance.
Multiple channel, low jitter GHz clock solutions that support ADCs with JESD204B outputs continue to proliferate in the industry. We get questions from design engineers about how to select the right clock solution for their GSPS ADCs. Below are answers and analysis to some common discussions regarding the technical impact of pairing a clock solution with a particular ADC.
Using high input frequencies to wideband GSPS ADCs in the 2nd or 3rd Nyquist zone requires lower jitter and high speed clocks. What is the impact of clock jitter on my ADC’s performance?
As higher frequency input signals are used in systems with the adoption of GSPS ADCs and direct RF sampling, the impact of clock jitter on system performance becomes more critical. A fixed amount of clock jitter may not impose any limitations on system performance with low frequency inputs. As ADC input frequencies increase, the same fixed amount of clock jitter will eventually have an impact on the signal-to-noise ratio (SNR) of the system. The SNR from an ADC is defined as the log ratio of the signal power to the total nonsignal power, or noise, that is seen at the input to the ADC.
The ADC sample instant with a known amount of clock jitter will create a larger or more ambiguous sample voltage delta (dV) when sampling a faster rise time signal at a higher frequency. This is due to the faster slew rate of higher frequency signals as compared to lower frequency signals. An example of this can be seen in Figure 1.
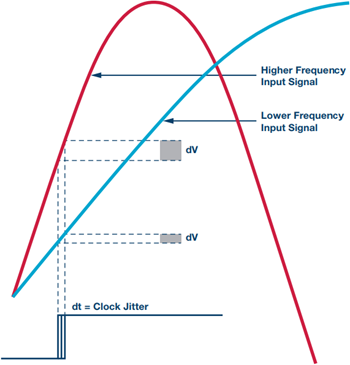
Figure 1.
With a fixed amount of clock jitter (dt) seen at the ADC clock, a higher frequency input signal will have a larger sampled voltage error, dV, relative to a lower frequency input signal. This will have a direct impact on the dynamic range capability of the ADC.
What is the difference between peak-to-peak and rms (root mean squared) jitter?
There are two categories of jitter on a clock signal that can impact an ADC’s performance: random jitter (RJ) and deterministic jitter (DJ). Deterministic jitter comes from an identifiable interference signal and has an amplitude that is bounded in magnitude. It is created by all other unwanted signal characteristics such as crosstalk, electromagnetic interference (EMI) radiation, supply noise, and periodic modulation such as simultaneous switching. Deterministic jitter will appear as spurious signals on the clock signal. These unwanted signals will also show up as spurious on the digitized spectrum from the ADC.
Random jitter is unbounded and Gaussian in magnitude. It can be created by influences that are less predictable, such as temperature and small semiconductor process variations. If there is enough random jitter present on an ADC sample clock, it may raise the noise spectral density (NSD) power on the data converter. The magnitude of each RJ and DJ root square summed (RSS) together will determine the total jitter impact on the ADC sample clock.
A histogram of the random jitter magnitude on a typical clock signal should have a purely normal Gaussian distribution. Any additional deterministic component to the jitter will create a bimodal distribution. Peak-to-peak jitter is measured by taking a large population of timing measurements and determining the absolute smallest and largest jitter variation. As more measurements are taken, the minimum and maximum jitter will eventually continue to expand the absolute peak- to-peak value. A practical measurement must be bounded at some point in time and measurement sample quantity. Therefore, an absolute peak-to-peak jitter value is not particularly useful, unless it is based on a Gaussian distribution with a known standard deviation.
The rms jitter is the value of one standard deviation within a Gaussian plot. This value will stay relatively stable, even as the measured sample size increases. It also makes the rms jitter value more meaningful than the peak-to-peak jitter and easier to measure. For the rms jitter to have a meaningful magnitude, the total jitter must have a Gaussian profile. Otherwise, a distorted Gaussian profile will identify that a deterministic jitter component is present. If possible, the root cause of the deterministic jitter component should be identified and mitigated or removed.
Although an ideal clock signal would have all of its power reside in a single frequency bin, real-world clock solutions will have some magnitude of “phase noise skirt.” A clock signal with only random jitter will form a Gaussian distribution. Any deterministic jitter will distort the ideal Gaussian profile. The phase noise power at any point on the curve can be measured from its peak at F0 to a frequency bin of interest at F0 + Fm.
How can the SNR and NSD be degraded by the ADC’s input clock jitter?
An ADC’s NSD is one of the main performance metrics of a converter. NSD defines the entire noise power, per unit of bandwidth, sampled at the corresponding ADC sample frequency (fS). NSD is a function of the full-scale signal-to-noise ratio (SNRFS) of an ADC, with any clock jitter degradation, and the Nyquist bandwidth (fS/2) in which the noise is spread across the spectrum. Any sampling instant error will degrade some portion of the signal power to noise.
As clock jitter increases, some portion of the sampled signal power of interest is spread outside of its discrete frequency bin in a fast Fourier transform (FFT) and subsequently becomes part of the noise power. This is due to the nonideal sampling instant of the signal by the phase noise of the clock signal. Figure 2 shows a visual example of how phase noise “skirts” bleed off power from the desired signal of interest in the frequency domain.

Figure 2.
Ideal NSD performance for an ADC operating at 1 GSPS limited by its rms encode clock jitter. The rms jitter of the clock can limit the ADC’s dynamic range at higher input frequencies.

Figure 3.
To find the total SNR degradation of an ADC, compute the root sum square of the jitter noise power and the published SNR of the ADC at the signal frequency of interest. When the ADC sampling clock jitter is sufficiently low, the SNRadc = SNRdegradation as the internal aperture jitter and nonlinearities of the converter will limit its SNR. Conversely, a sampling clock with increasing jitter will eventually become the limiting factor in the SNR performance of the ADC. This will be more pronounced as the signal of interest is higher in frequency. Output noise for all realizable ADCs is limited by SNR performance. As the input level is increased or decreased, the jitter noise component changes accordingly.
The NSD of the ADC can be computed based on the full-scale input power to the ADC minus the SNR degradation and the noise power, which is a function of the Nyquist rate. This can be seen in the equation below.

This plot shows a 14-bit wideband converter that is limited to an NSD of –155 dBFS/Hz at low (<100 MHz) analog input frequencies by the internal ADC quantization, and linearity, regardless of external rms clock jitter up to 200 fs. In this case, the system clock jitter will dictate NSD performance at higher analog input frequencies (>100 MHz) depending upon its rms magnitude.
As an example, Figure 4 shows the NSD impact of a 14-bit 1 GSPS ADC, with various clock jitter, across a wide input bandwidth. When sampling a signal from 10 MHz to 100 MHz, even a relatively high clock jitter of 200 femtoseconds will not appreciably impair the ADC’s NSD performance of –155 dBFS/Hz. However, when sampling a 1 GHz or 2 GHz input signal, the same 200 fs rms jitter of the clock will significantly limit the ADC performance when compared to lower rms clock jitter. When sampling a 2 GHz signal, an rms jitter of 200 fs will have a 12 dB increase in the ADC noise, relative to the signal power of interest, compared to an rms clock jitter of 50 fs.

Figure 4.
Some GSPS ADCs allow a faster input clock multiple that can be divided down within the ADC to derive the actual sample clock. What are the benefits and tradeoffs of using a higher rate sample clock to my ADC in this case?
Instead of only allowing an option to input a clock frequency at 1× the actual sample rate, some ADCs allow a higher multiple clock rate to be used, such as 2×, 4×, or 8× the sample rate. The ADC can then be configured to internally divide down the higher frequency clock into a slower clock multiple that samples the analog signal to the ADC. There are a few perks to this type of configuration.
The first benefit is that a system board can now accommodate multiple sample rates using the same hardware and clock solution. A slight software register change to the ADC is all that is needed to use a faster or slower sample rate in this case. For example, an electrical test and measurement solution using an ADC with the highest clock rate, such as a digital sampling oscilloscope, can now offer end users the option of several sample rates with the touch of a GUI button. This also allows for marketing segmentation of the same boards with only a difference in software builds. Two ADCs that offer this feature are the AD9680 and the AD9234, 1 GSPS converters that have 14-bit and 12-bit resolution, respectively.
A second benefit is that the ADC performance can be better using a higher clock frequency than using the lower 1× sample rate. A higher frequency clock provides a faster slew rate of the signal and therefore inherently a more accurate edge and lower jitter. As discussed before, the lower jitter clock will inherently allow a lower NSD and higher SNR, provided that the ADC jitter is not the limiting performance factor.
A third benefit is to eliminate one additional clock frequency from the clocking device and routing on the board. This allows the system to operate with fewer clock signal multiples and reduces the clocking complexity in general. An RF clock signal may be used as an input to some ADCs that permit the internal divide function for a slower sample clock.
One potential challenge to this sampling configuration is the need to identify the actual clocking device that is capable of low jitter at the increased frequency multiples. As clocking solutions with higher frequency, performance, and channel count are released and make their way to new system boards, this challenge is somewhat mitigated. However, the insatiable need for higher sample rate converters and complex companion clocking devices continues unabated.
How can I take a frequency domain phase noise plot from my clock device and determine the time domain rms jitter for my particular ADC sample clock frequency?
Although both describe the same phenomenon, it can be somewhat counterintuitive to relate a clock’s phase noise to that of a particular jitter value. While the two are interrelated, an engineer needs to cross the frequency and time domain chasm to correspond one to the other. The phase noise plot is charted in the frequency domain, while a clock signal’s rms jitter component is reflected as a time domain value.
Multiplication in the time domain is analogous to convolution in the frequency domain. Any phase noise skirt or phase modulated spurious noise on the clock will convolve to the digitized signal that is presented to the ADC. The level or magnitude of the noise convolution on the clock coupling to the sampled output is illustrated in the equation below.

An example phase noise plot of a clock signal is shown in the frequency domain in Figure 5. The x-axis shows the frequency offset relative to the carrier, which in this case is the clock at 983 MHz. The y-axis is the phase noise density expressed in dBc/Hz (the power in dB relative to the carrier power in units of Hertz). It should be clear from this plot that as we observe phase noise further in frequency from the clock, a relative floor is created and the magnitude of increasing cumulative phase noise is diminished.

Figure 5.
This plot shows the phase noise in units of dBc/Hz across a frequency offset from a carrier clock with frequency of 983 MHz. From this information, the clock jitter can be derived.
The rms jitter from a clock signal can be computed from a phase noise plot by integrating the area under the curve in a piecewise fashion per frequency decade. Although there are online calculation tools that can now compute the jitter from the phase noise, it can also be done with just a few math equations.
It would be impractical to attempt a computation of the exact jitter by summing the power of each 1 Hz offset bin. Therefore, by taking each frequency decade’s respective phase noise slope, in dB/decade between the endpoints, a very close approximation of the rms jitter can be realized. Ideally, the wideband phase noise should be integrated out to a large offset equal to the sample frequency. However, to keep a demonstration calculation bounded we can compute the rms jitter within a typical wireline application. Let’s take the phase noise plot from Figure 6 and compute the jitter within a 10 kHz to 20 MHz offset on a carrier of 983 MHz.

Figure 6.
A decade piecewise plot of the phase noise seen in Figure 5 is broken down into three segments to compute the rms jitter between an offset of the carrier 983 MHz frequency from 10 kHz to 20 MHz.
The total rms jitter is the sum of the area under the curve between the two frequency points of interest. In this case, the approximated area is shown within three segmented pieces labeled A, B, and C. The slope of the phase noise curve between the endpoints of each segment can easily be approximated and will be used for the calculation. The relationship between the period jitter, JPER, across the entire phase noise spectrum, L(f), can be described as:

RMS JPER within a certain frequency band between (f2 – f1) can be calculated by:

The phase noise can be approximated by using a piecewise function when the frequency axis of L(f) is in log scale. Therefore, L(f) can be written as:

where K-1 is the number of pieces in the piecewise function, b is the phase noise magnitude for the starting frequency of the decade, a is the approximated slope in units of dB/decade, and U(f) is the step function.
If we substitute L(f) shown in Equation 3 into Equation 2, we have:

We can then compute the rms jitter with the values from each piece of the Figure 6 plot with fc = 983 MHz:
A: a = –3.44 dB/decade starting at f = 10 kHz, b = –116.91 dBc/Hz
B: a = –9.75 dB/decade starting at f = 100 kHz, b = –120.35 dBc/Hz
C: a = –18.58 dB/decade starting at f = 1 MHz and ending at 20 MHz, b = – 130.1dBc/Hz
RMS JPER = 151 femtoseconds
The latest GSPS ADCs are using the JESD204B serial output instead of multiplexed banks of LVDS outputs. How can a clock solution also help align multiple ADCs within a system to a single sample using JESD204B?
A multiple channel, low jitter GHz clock solution can pair a system reference timing signal with each of its clock outputs as defined by the signal named SYSREF within the JESD204B specification. The SYSREF signal is the absolute timing reference for the JESD204B links used within the system. Several instrumentation, sensor array, and radar systems need multiple (2, 4 , 8, 16 … 100s) of synchronous ADCs that are time aligned to within as few samples as possible. For these type of applications, the timing flexibility of the clock solution is invaluable to deskew and align the SYSREF signal to each corresponding ADC clock.

Figure 7.
Multiple clock output pairs can be skewed in phase relative to one another as well as their associated companion SYSREF signals. Both coarse and fine timing adjustments allow the clock and SYSREF to be synchronized across an array of ADCs.
A system with 16 ADCs may require four separate boards that each use four ADCs and are indirectly connected together through an electrical backplane. Depending upon their spatial location to one another and the skew between the routing, each ADC may see its relative sample clock edge instant at a different moment in time.
In some cases, the clocks and associated SYSREF need to be aligned to the same point in time at each respective ADC. In other systems, the clock phases need to be intentionally misaligned in order to account for input signal phase differences across an array of ADCs. For interleaving of two or four ADCs, the clocks may need to be inverted or phase adjusted for particular 90° increments. In any case, a JESD204B clock solution can provide the independent skew capability between each ADC clock and SYSREF pair to achieve the purpose of the acquisition system.

Figure 8.
For JESD204B ADCs and DACs, new clock chip solutions can align multiple outputs to either a single-shot or a periodic SYSREF signal. This capability can null out the flight time difference due to spatial clock routing delays between the ADC acquisition instant and the clock source.
What are some available clock solutions for GSPS ADCs?
The phase noise, or time domain jitter, of a GHz clock solution will be the primary performance factor in selecting a clocking source for a GSPS ADC. For those acquisition systems that need a plethora of ADCs, the best clocking solutions also need to provide many output channels to drive their encode rates respectively. A secondary performance aspect is the synchronization ability using the system reference parameters within the JESD204B link that will further advance the capabilities of the clocking system.
The AD9525 provides seven output clock pairs at 3.3 GHz with an rms jitter of just 50 fs and a dedicated sync output that can be used as a SYSREF within the framework of the JESD204B interface. The AD9528 provides seven output clock pairs at 1 GHz, but also provides companion SYSREF signals than can be deskewed per clock pair to align their corresponding ADCs within a single sample alignment pulse. The HMC7044 is a high performance 3 GHz 14 output jitter attenuator with JESD204B SYSREF support.
Conclusion
The latest high bandwidth and wideband ADCs require an ever decreasing magnitude for their encode clock phase noise and jitter. Although many clock solutions can potentially be chosen for use with these high frequency ADCs, those with sufficiently low phase noise for the bandwidth of interest and the ability to synchronize many ADCs offer the best solutions.
A phase noise plot of a typical clocking solution can be translated into the time domain to determine its rms jitter and potential impact on an ADC’s dynamic range. An additional benefit of advanced clocking solutions includes unique SYSREF to clock signal pair deskew within the JESD204B framework. The critical selection of the companion clock component for GSPS ADCs can potentially maintain or degrade the performance of the ADC, based upon the acquisition signal frequency of interest.
About the Authors
Related to this Article
Products
JESD204B/JESD204C Clock Generator with 14 LVDS/HSTL Outputs
Low Jitter Clock Generator Eight LVPECL Outputs




















