Abstract
Transimpedance amplifiers (TIAs) are widely used to translate the current output of sensors like photodiode-to-voltage signals, since many circuits and instruments can only accept voltage input. An operational amplifier with a feedback resistor from output to the inverting input is the most straightforward implementation of such a TIA. However, even this simple TIA circuit requires careful trade-offs among noise gain, offset voltage, bandwidth, and stability. Clearly stability in a TIA is essential for good, reliable performance. This application note explains the empirical calculations for assessing stability and then shows how to fine-tune the selection of the feedback phase-compensation capacitor.
A similar version of this article appeared in the October 28, 2011 issue of Electronic Design magazine.
Wild Oscillations: Why Do They Happen?
Figures 1 to 3 show some basic TIA circuits. Figure 1 is popularly used in dual-supply systems. Figure 2 is a minor modification of this circuit for single-supply applications. The resistive-divider formed by R1 and R2 ensures that the output node of the op amp is higher than the Output Voltage Low specification during a no-light condition when only a small dark current flows through the photodiode. By ensuring that the op amp's output stage operates in the linear region, this offset improves both photo-detection in low-light conditions and response speed. However, care must be taken to keep this bias voltage on the IN+ pin small. Otherwise reverse-leakage current in the photodiode can degrade linearity and increase offset drift over temperature. In some applications the circuit in Figure 3 is used where the photodiode is placed directly across the input terminals of the op amp. This circuit avoids the reverse bias across the photodiode, although it requires a buffered reference. The reference must be fast enough to sink the photodiode current as required by the application. This, in turn, implies that amplifier A1 must be as fast as amplifier A2.

Figure 1. Basic TIA circuit (dual supply).

Figure 2. Basic TIA circuit of Figure 1 modified for a single supply.

Figure 3. Basic TIA circuit of Figure 2 modified for single supply.
Like any op amp circuit with feedback, each of the above circuits can be separated into an amplifier with open-loop gain, AVOL, and a feedback network comprised of the resistance and the photodiode. Figure 4 shows the equivalent circuit of the photodiode in Figures 1 to 3.¹ For most photodiodes, RSERIES = 0 and RSHUNT = Infinity is a fair approximation. Consequently, the simplified model reduces to the short-circuit current source in parallel with the junction capacitance. This simplified photodiode model will be used for subsequent stability analysis.

Figure 4. Photodiode equivalent circuit: IP = photocurrent; RSHUNT = diode shunt junction resistance; CJ = junction capacitance; and RS = series resistance.
To understand why the circuits in Figures 1 to 3 might oscillate, it is useful to plot the frequency of the open-loop gain and the feedback factor. Figure 5 plots the open-loop gain response of the op amp. It is constant from DC until the dominant-pole corner frequency; it decreases at 20dB per decade thereafter until it reaches the second-pole corner. Mathematically, the single-pole response can be represented as:

Where:
AVOL = DC open-loop gain
AVOL(jω) = open-loop gain corresponding to frequency, ω
ωPD = dominant-pole frequency in radians/seconds
Using the simplified equivalent circuit for the photodiode, the feedback network is simply a one-pole RC filter comprised of the feedback resistance, RF, and the total input capacitance, Ci (junction capacitance of the photodiode in parallel with the input capacitance of the op amp). The feedback factor is given as:

Therefore, the reciprocal of the feedback factor is:
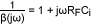
Figure 5 also plots the response curve for 1/β(jω). At low frequencies the curve remains flat at unity gain, as expected from the unity-gain resistive feedback. It then rises at 20dB/dec starting from the corner frequency, fF.

Figure 5. Open-loop gain, AVOL(jω), and the reciprocal of feedback factor, 1/β(jω), versus frequency. The rate of closure between the two curves determines the likelihood of oscillations/ringing.
From the Barkhausen stability criterion, oscillation can result if the closed-loop TIA circuit does not have sufficient phase margin for Aβ ≥ 1. Hence, the intersection of the AVOL(jω) response curve with the 1/β(jω) curve denotes a critical intercept fundamental for stability analysis. The phase margin at this intersection frequency can be determined by observing the rate of closure between the two response curves, AVOL(jω) and 1/β(jω). If the rate of closure of the two response curves is 40dB, as seen in Figure 5, the circuit will be unstable. There is another intuitive way to understand this. At lower frequencies the phase shift in the feedback signal is 180 degrees due to the inverting nature of the negative feedback. As the frequency increases well into the -20dB/dec slope region of AVOL, the dominant pole of the op amp can add up to 90 degrees of phase shift. Similarly, the pole introduced by the feedback network can add another 90 degrees of phase shift, thus producing a phase shift of about 360 degrees at Aβ = 1. If the phase shift is 360 degrees, self-sustaining oscillations will result. If the phase shift is close to 360 degrees, heavy ringing is observed. In either case, some form of phase compensation scheme will be required to stabilize the circuit.
No Evil Is Without Its Compensation: Feedback Capacitor Calculations
It is common knowledge that adding a bypass capacitor in parallel with the feedback resistance provides the requisite compensation to guarantee sufficient phase margin (Figure 6). It is important to calculate the value of the feedback capacitor required to provide optimal compensation. To account for the added phase-compensation capacitor, substitute ZF in Equation 2 with RF || CF. The feedback factor now becomes:

Comparing Equation 2 and Equation 4 shows that the addition of capacitor CF introduces a zero in the feedback factor, besides modifying its pole. The zero compensates for the phase shift introduced by the feedback network. This can be seen graphically in Figure 7. If the phase shift is overcompensated by choosing a large feedback capacitor, then the rate of closure can be reduced to 20dB per decade (90 degrees phase margin). However, overcompensation also reduces the usable bandwidth of the TIA. While a reduced bandwidth may not be an issue with low-frequency photodiode applications, high-frequency or low-duty-cycle pulsed photodiode circuits definitely need to maximize the available bandwidth. For such applications, the goal is to find the minimum value of the feedback compensation capacitor, CF, needed to eliminate oscillation and minimize ringing. However, it is always a good idea to overcompensate the TIA circuit slightly. Overcompensation is recommended to provide sufficient guardband to account for up to ±40% variation in an op amp's bandwidth over process corners and the tolerance of the feedback capacitor.

Figure 6. Phase compensation capacitor CF helps improve stability.

Figure 7. Phase response with the phase-compensation capacitor, CF.
A good design compromise is to target 45 degrees of phase margin at the intercept of the AVOL(jω) and 1/β(jω) curves. This margin requires the optimum value of CF to be calculated so that the added zero in the feedback factor, β(jω), is located at the frequency corresponding to Aβ = 1, as shown in Figure 7. One equation for the intercept frequency is:

Equation 5 has two unknowns, the intercept frequency, fi, and the feedback capacitor, CF. To solve for CF, we need to find another simultaneous equation. One way to obtain the second equation is to equate the AVOL(jωi) and 1/β(jωi) curves. The resulting equation is complicated and does not lend itself to an easy solution. The graphical approach for solving CF is a more convenient alternative.² Observing Figure 7, both curves have a slope of 20dB/dec. Therefore, the approximate triangle formed by both curves with the horizontal axis is isosceles. Hence, the intercept frequency, fi, is the average of the other two vertices. Since the frequency is plotted in the logarithmic scale, we have:

Here:

Where fGBWP = unity gain bandwidth of the op amp. To account for the variation in unity-gain bandwidth over process corners, select fGBWP to be 60% of the value specified on the op amp's data sheet.
For decompensated op amps, use fGBWP to equal 60% of the frequency at which the projection of the -20dB AVOL(jωi) slope intersects the 0dB x-axis line.
With some algebraic manipulation, Equation 6 can be rewritten as:

Equation 8 shows that the intercept frequency, fi, is equal to the geometric mean of the unity-gain bandwidth, fGBWP, and the pole-corner frequency, fF, of β(jω). Substituting for fF from Equation 7, we get:

Equating Equations 5 and 9 and squaring, we get:

The above quadratic equation can be easily solved to calculate the following value of CF:

The calculated value of the feedback capacitor CF is valid for both large-area and small-area photodiodes.
Alright...Give Us the Scope Now: Design Example
TIAs are used in a variety of applications such as 3D goggles, compact disc players, pulse oximeters, IR remote controls, ambient light sensors, night-vision equipment, and laser range finding.
Consider a rain-sensor application. Rain sensors are presently used in high-end automobiles to automatically adjust the wiper speed depending on the presence and intensity of rain. Usually the optical rain sensors operate on the principle of total internal reflection. The sensor is generally located behind the driver's rear-view mirror. An infrared light laser source beams the light pulses at an angle to the windshield. If the glass is not wet, then most of the light comes back to the photodiode detector. If the glass is wet, then some of the light is refracted and less light is detected by the sensor tuning on the wiper. The wiper speed is set based on how fast the moisture builds up between the sweeps.
Detecting the change in moisture for wiper adjustment while rejecting the low-frequency, ambient-light IR content requires the rain sensor to operate at a pulse frequency over 100Hz. For example, consider the problem of designing a TIA for the rain sensor with the following specifications:
Photodiode IR current pulse peak amplitude = 50nA up to 10µA, depending on reflected light content
ON time duration = 50µs
Duty cycle = 5%
RF = 100kΩ
BPW46 photodiode is used
Table 1 lists some low-noise, CMOS input, Maxim op amps are popularly used in TIA circuits in a wide variety of applications. For this design example, we select the MAX9636 op amp. The MAX9636 is also suitable for other battery-powered, portable equipment since its design is a good trade-off between lower quiescent current and noise performance. For higher-bandwidth applications, op amps like the MAX4475 and MAX4230 might be more suitable.
| Part | Input Bias Current (pA) | Input Voltage Noise (nV/sqrt(Hz)) | Supply Current (µA) | Unity Gain Bandwidth (MHz) | Smallest Package | Features |
| MAX9636 | < 0.8 | 38 at 1kHz | 36 | 1.5 | SC70 | Low power, low bias current, high GBW to supply current ratio, low cost |
| MAX9620 | < 80 | 42 at 1kHz | 59 | 1.5 | SC70 | Precision, low power, high GBW-tosupply current ratio |
| MAX9613 | < 1.55 | 28 at 10kHz | 220 | 2.8 | SC70 | Low bias current at VCM = VEE, VOS selfcalibration |
| MAX4475 | < 1 | 4.5 at 1kHz | 2200 | 10 | SOT23, TDFN | Ultra-low noise |
| MAX4230 | < 1 | 15 at 1kHz | 1100 | 10 | SC70 | High bandwidth, low noise |
| MAX9945 | < 0.15 | 16.5 at 1kHz | 400 | 3 | TDFN | High voltage, low power |
| MAX4250 | < 1 | 8.9 at 1kHz | 400 | 3 | SOT23 | Low noise and low distortion |
| MAX4238 | < 1 | 30 at 1kHz | 600 | 1 | SOT23, TDFN | Precision and low drift |
| MAX4400 | < 1 | 36 at 10kHz | 320 | 0.8 | SC70 | Low cost |
The estimated value of feedback capacitance is calculated by substituting the following parameters in Equation 10:
Ci = junction capacitance of photodiode (70pF) + 2pF input capacitance of the MAX9636 = 72pF
fGBWP = 0.9MHz.
Gain bandwidth is not a trimmed parameter and can vary ±40% over process corner for any op amp. Consequently, even though the data sheet specifies the typical unity gain bandwidth to be 1.5MHz, we have considered the unity gain bandwidth to be 60% of this typical value in order to account for process variations.
Here, RF = 100kΩ.Therefore, the calculated value of CF = 15.6pF. The next highest standard value of the capacitor is 18pF.
Figure 8 shows the output of the TIA without any compensation feedback capacitor and using the circuits in Figures 1 to 3. As expected, oscillation is observed with no phase compensation capacitor. If CF = 10pF is used, then ringing stops, although an overshoot is still visible as seen in Figure 9. Next the feedback capacitor value is increased to the recommended calculated value of 18pF. Figure 10 shows that no ringing or oscillation is observed for the CF = 18pF case, thus validating the theoretical analysis above. Figure 11 shows the corresponding small signal-step response with 50nA amplitude of photodetector current.

Figure 8. MAX9636 output with RF = 100kΩ, CF not installed, and a 10µA input current pulse.

Figure 9. MAX9636 output with RF = 100kΩ, CF = 10pF, and a 10µA input current pulse.

Figure 10. MAX9636 output with RF = 100kΩ, CF = 18pF, Ci = 72pF, and a 10µA input current pulse.

Figure 11. MAX9636 output with RF = 100kΩ, CF = 18pF, Ci = 72pF, and a 50nA input current pulse. Waveform is AC-coupled in order to zoom in.
This article demonstrates the theory and calculations to compensate and stabilize a TIA circuit. A good match was observed between theoretical and lab results.
Related to this Article
Products
SOT23, Low-Noise, Low-Distortion, Wide-Band, Rail-to-Rail Op Amps
3V/5V Low-Power, Low Input-Bias, CMOS, Rail-to-Rail I/O Op Amps
UCSP, Single-Supply, Low-Noise, Low-Distortion, Rail-to-Rail Op Amps
38V, Low-Noise, MOS-Input, Low-Power Op Amp
Low-Power, High-Efficiency, Single/Dual, Rail-to-Rail I/O Op Amps
Ultra-Low Offset/Drift, Low-Noise, Precision SOT23 Amplifiers




















