ADSP-CM403 HAE—Harmonic Analysis in Solar Applications

Introduction

A solar PV inverter converts power from a solar panel and deploys this power to the utility grid efficiently. Solar PV inverters of older days were simply modules that dumped power onto the utility grid. However, new designs require solar PV inverters to contribute to the stability of the grid.

This article will review how new ADI technology in the form of a HAE (Harmonic Analysis Engine) improves smart grid integration and monitor power quality on the grid, thus contributing greatly to the stability of the grid.

Smart Grid

What is a smart grid? IMS Research defines a smart grid as “a utility supply infrastructure with the inherent ability to match and manage generation and consumption efficiently, while obtaining maximum benefits from the available resources.” For the new generation of solar PV inverters to attach onto a smart grid, more and more intelligence is required in the inverter to achieve this. This in itself is a concern mainly due to the imbalances that may be created as a result of too many grid connections when demand is not there to meet that being supplied on to the grid. Based on this, as mentioned earlier, solar PV inverters will need more intelligence, and the focus of this intelligence needs to be on grid integration, where systems will need to aid in the ability to stabilize the grid as opposed to serving as a simple power supplier to the grid.

Figure 1. ADSP-CM403 HAE Block Diagram, Analog Devices.

This requires better measurement, control, and analysis of the quality of the power injected onto the grid. Of course, this leads to new directives and higher technical requirements, which in turn directly translates into new technology.

ADSP-CM403XY HAE Peripheral Block

The HAE block is essentially a digital PLL simplified as shown below. The HAE receives V and I data continuously and after several cycles will lock onto the fundamental of the input waveform. The input range of the HAE block is 45 Hz to 66 Hz. Up to 40 harmonics can be analyzed, 12 at a time. For each harmonic the PLL will attempt to lock onto the required signal.

The harmonic engine hardware block works in conjunction with the harmonic analyzer to co-process results. As the harmonic engine produces results in their final formats, they are stored in the results memory. The HAE engine computes harmonic information in a no-attenuation pass band of 2.8kHz (corresponding to a –3 dB bandwidth of 3.3 kHz) for line frequencies between 45 Hz and 66 Hz.

Figure 3. Frequency Pass-Band of the HAE.

Neutral current can also be analyzed simultaneously with the sum of the phase currents. At the start of a new sampling period, the harmonic engine cycles through predefined locations in data RAM, which contain the analyzer processing results. The contents are then further processed, if needed.

Voltage and current data can be received from the sinc block or the ADC (both stored in SRAM) and input into the HAE block at an 8 kHz rate. An interrupt can be generated at this 8 kHz rate to advise the solar PV inverter to input available data. When the data is analyzed and those calculations below are computed, the HAE block will generate another interrupt to advise the solar PV system that the harmonic analysis data is ready for display. The ADSP-CM403 can also direct the HAE to DMA all results to SRAM where the system code can then display the results. This results in little code overhead for the entire HAE system.

ADSP-CM403XY HAE Results

The HAE results in Figure 4 show clearly which harmonics are present in the system when looking at the voltage rms data. The fundamental at 50 Hz is clearly present, however the lower harmonics at 250 Hz and 350 Hz (i.e. harmonics 5 and 7) have some presence in this example result set.

Figure 4. V rms Sample Results from the HAE for Harmonics 1–12.

The specific equations used in these calculations are shown below, for both fundamental and harmonic calculations.

Harmonic Engine Outputs and Registers where Values are Stored

Table 1. HAE Mathematical Calculations
Quantity	Definition	HAE Registers
RMS of the Fundamental Component	V₁,I₁	F_VRMS, F_IRMS
RMS of the Harmonic Component	V_n,I_n,n = 2,3,...,12	Hnn_VRMS, Hnn_XIRMS
Active Power of the Fundamental Component	P₁ = V₁I₁cos( φ₁ - γ₁)	F_ACT
Active Power of the Harmonic Component	P_n = V_nI_ncos(φ_n - γ_n), n = 2,3,...,12	Fnn_ACT
Reactive Power of the Fundamental Component	Q₁ = V₁I₁sin(φ₁ - γ₁)	F_REACT
Reactive Power of the Harmonic Component	Q_n = V_nI_nsin(φ₁ - γ₁), n = 2,3,...,12	Hnn_REACT
Apparent Power of the Fundamental Component	S₁ = V₁I₁	F_APP
Apparent Power of the Harmonic Component	S_n = V_nI_n, n = 2,3,...,12	Hnn_APP
Power Factor of the Fundamental Component		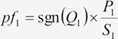F_PF
Power Factor of the Harmonic Component		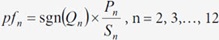Hnn_PF
Harmonic Distortion of a Harmonic Component		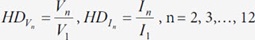Hnn_VHDN, Hnn_IHDN

Programming Example

INT HAE_CONFIG(VOID)
{ INT I;

HAE_INPUT_DATA(VOUTPUT, SINC_VEXT_DATA);
HAE_INPUT_DATA(IOUTPUT, SINC_IMEAS_DATA);

RESULT = ADI_HAE_OPEN(DEVNUM, DEVMEMORY, MEMORY_SIZE, &DEV);
RESULT = ADI_HAE_REGISTERCALLBACK(DEV, HAECALLBACK, 0);
RESULT = ADI_HAE_SELECTLINEFREQ(DEV, ADI_HAE_LINE_FREQ_50);
RESULT = ADI_HAE_CONFIGRESULTS(DEV, ADI_HAE_RESULT_MODE_IMMEDIATE, ADI_HAE_SETTLE_TIME_512, ADI_HAE_UPDATE_RATE_128000);
RESULT = ADI_HAE_SETVOLTAGELEVEL (DEV, 1.0);
RESULT = ADI_HAE_ENABLEINPUTPROCESSING(DEV, FALSE, FALSE); /* FILTER ENABLED */
/* ENABLE ALL HARMONICS (IN ORDER) */
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_1, 1);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_2, 2);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_3, 3);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_4, 4);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_5, 5);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_6, 6);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_7, 7);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_8, 8);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_9, 9);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_10, 10);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_11, 11);
RESULT = ADI_HAE_HARMONICINDEX (DEV, ADI_HAE_HARMONIC_INDEX_12, 12);

RESULT = ADI_HAE_SUBMITTXBUFFER(DEV, &TXBUFFER1[0], SIZEOF(TXBUFFER1));
RESULT = ADI_HAE_SUBMITTXBUFFER(DEV, &TXBUFFER2[0], SIZEOF(TXBUFFER2));
RESULT = ADI_HAE_ENABLEINTERRUPT(DEV, ADI_HAE_INT_RX, TRUE);
RESULT = ADI_HAE_ENABLEINTERRUPT(DEV, ADI_HAE_INT_TX, TRUE);
RESULT = ADI_HAE_CONFIGSAMPLEDIVIDER(DEV, 100000000);
RESULT = ADI_HAE_RUN(DEV, TRUE);
// RESULT = ADI_HAE_CLOSE(DEV);

}

/* EVENTS */

VOID HAECALLBACK(VOID* PHANDLE, UINT32_T EVENT, VOID* PARG) /* ISR ROUTINE TO LOAD / UNLOAD DATA FROM HAE

{

UINT32_T N;
ADI_HAE_EVENT EEVENT = (ADI_HAE_EVENT)EVENT; /* RESULTS RECEIVED FROM HAE 128MS */
IF (EEVENT == ADI_HAE_EVENT_RESULTS_READY)

{ /* GET RESULTS */

PRESULTS = (ADI_HAE_RESULT_STRUCT*)PARG; /* POINTER TO TXBUFFER1 OR TXBUFFER2 */

/* DO SOMETHING WITH THE RESULTS */
FOR (N=0; N<NUM_CHANNELS; N++)

{

IRMS[N] = PRESULTS[N].IRMS;

VRMS[N] = PRESULTS[N].VRMS;
ACTIVEPWR[N] = PRESULTS[N].ACTIVEPWR;

}