Measurement and Control of RF Power (Part III)
Read other articles in this series.
Log amps are generally specified for a sine wave input. Like diode detectors, log amps are not true rms responding. Differing signal waveforms in a log amp shift the effective value of the log amp’s intercept upwards or downwards. Graphically, this looks like a vertical shift in the log amp’s transfer function (see Fig. 19.), the logarithmic slope being unaffected. The figure shows the transfer function of the AD8307 when alternately fed by an un-modulated sine wave and by a forward-link CDMA channel of the same rms power (9 channels active.) The output voltage differs by the equivalent of 3.55dB (88.7 mV) over the complete dynamic range of the device.

Fig. 19: Shift In Log Amp Transfer Function With Signal Crest Factor
The table shows the correction factors that should be applied to measure the rms signal strength of various signal types with a logarithmic amplifier which has been characterized using a sine wave input. So, to measure the rms power of a square-wave, for example, the mV equivalent of the dB value in the table (-3.01 dB which corresponds to 75.25 mV in the case of the AD8307) should be subtracted from the output voltage of the log amp. In practical applications where the input signal to the log amp is constant (but something other than a sine wave) the log amp can simply be calibrated to that signal type, that is, we pay no attention to what the output level would be for a sine wave input -- because the device will never encounter one.
| Signal Type |
Correction Factor (add to output reading) |
| Sine wave |
0 dB |
| Square Wave or dc |
-3.01 dB |
| Triangular Wave |
+0.9 dB |
| GSM channel (all time slots on) |
+0.55 dB |
|
CDMA channel (Forward Link, 9
channels on)
|
+3.55 dB |
| CDMA Channel (Reverse Link) | +0.5 dB |
| PDC channel (all time slots on) | +0.58 dB |
| Gaussian Noise |
+2.51 dB |
RMS To DC Converters
The AD8361 (see Fig. 20) is a low power rms-responding detector for use in high frequency receiver and transmitter signal chains, up to 2.5GHz. The AD8361 performs an explicit root-mean square computation.

Fig. 20: Rms to Dc Converter
The RF input signal, which can have a frequency up to 2.5 GHz, is applied to a wideband squaring circuit. An on-board 50 pF capacitor filters the output of the squarer. Additional filtering can be supplied by connecting an external capacitor to the FLTR pin. The filtered output of the squarer circuit is applied to a square-rooting circuit. This circuit consists of an operational amplifier type circuit with a second squaring circuit in its feedback loop. This results in the inverse function (i.e. square-root) in the forward direction. In addition, a resistive attenuator (1/6.5) in the feedback loop adds a gain in the forward direction of 7.5. So the overall transfer function of the device is given by the equation
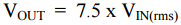
To get a linear transfer function (see Fig. 21) we plot output voltage on a log scale vs. input level in dBm (plotting Vout vs. Vin will also yield a linear function). You will note that this response has the same basic form as the diode detector plots we looked at earlier. The rms converter, however, has a linear operating region that is lower than that of a diode circuit and also delivers a higher output voltage level.

Fig. 21: Output Voltage Vs. Input Level For AD8361 Rms to Dc Converter
As before, to evaluate the temperature stability we do a linear regression of the measurement data at room temperature (this gives us a slope and intercept) and plot the deviation of the data at temperatures from this reference. This (Fig. 21, again) shows that the temperature stability degrades steadily with decreasing input level and has a drift range of about 2 dB (from cold to hot) for an input level of about -20 dBm.
Temperature Drift Compensation of RMS to DC Converter
The relatively low temperature drift of the AD8361 can be reduced further if the device temperature is known. Many systems incorporate a temperature sensor; the output of the sensor is typically digitized. Because the AD8361's output is also generally digitized this suggests the possibility of a software correction to the reading from the rms to dc converter. From a calibration perspective, the same two-point calibration at room temperature is still sufficient.
In the part-to-part distribution of temperature drift for a large number of AD8361 devices (see Fig. 22) the two bands show the deviation from room temperature to +85°C and -40°C. It is clear from this plot that the device's temperature drift is fairly consistent from part to part.

Fig. 22: AD8361 Rms To Dc Converter, Distribution Of Temperature Drift
The output voltage of the AD8361 at ambient (25°C) can be expressed by the equation:
![]()
where, GAIN is the conversion gain in V/Vrms and VOS is the extrapolated output voltage for an input level of 0 V. GAIN and VOS (also referred to as Intercept and Output Reference) can be calculated at ambient using a simple two point calibration, that is by measuring the output voltages for two specific input levels. Calibration at roughly 35 mV (-16 dBm ) and 250 mV (+1dBm) are recommended for maximum linear dynamic range. However, alternative levels and ranges can be chosen to suit the application. GAIN and VOS are then calculated for each device using the equations:
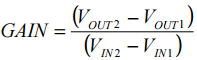
![]()
We can also write an expression for the ideal value of VIN for a particular value of VOUT:

This would be the ideal input level for a particular measured output level, assuming a completely linear detector.
Both GAIN and Vos drift over temperature. However, the drift of Vos has a bigger influence on the error relative to the output. But the offset error has a diminishing influence with increasing level on the overall measurement error (the number of mV/dB increases with input level just like a diode detector.) This explains the decreasing drift error with input level(see Figs. 21 & 22, again.)
The average drift of Vos is 0.43 mV/°C from -40°C to +25°C and 0.25 mV/°C from +25°C to +85°C4. For a less rigorous compensation scheme, the average drift over the complete temperature range can be calculated:

With the drift of VOS included, the equation for Vout becomes:
![]()
The equation can be rewritten to yield a temperature compensated value for VIN.
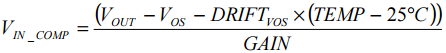
Now, if we plot VIN_COMP/VIN_IDEAl in dB, with respect to input level, we get an error plot for the transfer function after compensation has been applied (see Fig. 23.) This plot shows that over temperature and a dynamic range of 35 dB, there is a worst case error of approximately ±0.25 dB.

Fig. 23: AD8361 Over-Temperature Error After Error-Compensation Algorithm Has Been Applied
| +0.55 dB |
| +2.51 dB |
关于作者
关联至此文章
产品
250 MHz解调对数放大器

















