摘要
RFIC幅移键控(ASK)或者叫做开关键控(OOK)接收机的灵敏度对于远程无线开门系统(RKE)、轮胎压力监视系统(TPM)、家庭自动化系统以及其它应用系统的设计者来说是一项重要的规范。这类接收机一般工作在315MHz或433MHz的频段上,但是其电路对其它载波频率也是适用的。
了解这种接收机一些特性在理论上的极限值对RFIC用户和设计者都是很重要的,因为这样就能确定他们在设计上的改进是不是成功的。
本篇应用笔记描述了一种在已知系统噪声系数、IF带宽和基带带宽的条件下一步一步的计算ASK接收机灵敏度的方法。
结果表明,接收信号强度指示(RSSI)放大器实现的对数幅度检测在输入SNR较低时降低了输出信噪比(SNR) (门限效应),而灵敏度的提高与IF带宽与基带带宽之比的平方根成正比。
大多数现代幅移键控(ASK)接收机利用将调制的RF信号直接的或者经过一次或多次频率变换后通过一个幅度检测器对数据进行检测。幅度检测器基本上就是一个RF或IF放大器和一个RSSI (接收信号强度指示器),RSSI的输出与输入RF或IF信号功率的对数成正比。
因为RSSI检测器是一个非线性的检测器,它将改变输入信号的信噪比(SNR)。ASK灵敏度计算的关键就在于RSSI检测器的SNROUT与SNRIN关系曲线。
一旦我们知道了SNROUT与SNRIN之间的关系,在已知噪声系数、IF带宽和数据速率的条件下可以通过如下步骤找出ASK灵敏度
- 确定目标BER (在本例中为10-3)所需的Eb/No,然后根据Eb/No用下面的等式计算SNR。
- SNR = (Eb/No) * (R/BBW)
- 其中R是数据速率,BBW是数据滤波器的带宽
- 将上一步计算出来的SNR减去IF (预检波) BW与数据滤波器BW之比的dB数。例如, 如果IF BW为600kHz数据滤波器BW为6kHz,这就意味着要从SNR中减去20dB。得到的结果就是RSSI检测器输出信号的SNR,这一信号还没有被数据滤波器消除其高频噪声(假设这些噪声占据了IF BW)。对于灵敏度来说,这一比例通常是以dB为单位的负值。
- 用RSSI的SNROUT与SNRIN关系曲线找出RF或IF放大器和RSSI检测器输入信号的SNR。实际上就是通过这条曲线用第二步计算中得到 SNROUT “反向”推导SNRIN。
- 使用接收机前端SNR公式找出接收机输入端的信号水平。这就是灵敏度S
- S = (SNRIN) * (kTBIFFS)
- SNR = (Eb/No) * (R/BBW)
因为RSSI检测器是一个对数检测器,输入输出SNR的关系可以用一种封闭的方式表示,尽管可能看起来有点儿乱。一篇发表在IEEE学报上比较老的关于航空与电子系统的文章推导出了其表达式并画出了SNROUT与SNRIN关系的曲线。这篇文章中的曲线非常小而且没有足够的网格线,但是可以在Excel表格中对表达式进行分析计算并画出更具体的曲线图。这个曲线如下图所示,它与简单SNROUT = SNRIN曲线(线性检波)画在一起作为对比。注意门限效应。在两条线3.7dB的SNR “交点”以下,信号通过检测器后SNR变差了。在这个点以上的部分,信号通过检测器后SNR得到改善。

图1.
另一张Excel电子表格将上述步骤1到步骤4与SNROUT与SNRIN关系曲线相结合进行了如下图所示的灵敏度计算。图中曲线是在三个不同的IF带宽条件下灵敏度与数据速率关系的曲线,噪声系数取7dB。注意,灵敏度的改善是与IF BW或者数据速率的平方根成正比的。这是因为我们所计算的灵敏度处在RSSI SNR曲线中SNROUT比SNRIN的斜率约为对数坐标2的范围内(平方律关系)。
这些曲线与精心设计的ASK接收机的实际情况是一致的。例如,数据速率为3kbps、IF BW为280kHz的时候,灵敏度为-114dBm。根据ASK接收机10-3 BER的要求,在本计算中Eb/No取11dB。对于稳定的CW信号,SNR的计算结果是12dB (因为数据的平均占空因数为50%,所以“峰值” Eb/No为14dB,比BBW与数据速率1.5:1的比例小大约2dB)。
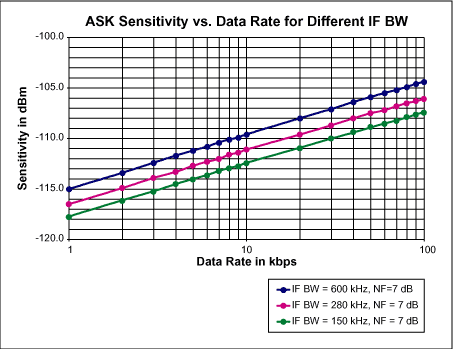
图2.
在此有必要指出所作的两个假设:(1) RSSI检测器输出的噪声带宽与IF带宽相同。(2) RSSI检测器输出的噪声为高斯分布。实际上,RSSI检测器的噪声带宽可能比IF带宽大许多,可以通过增加系统的实际噪声系数将这种情况计算在内。输出噪声的分布也不是高斯的,所以完整彻底的分析需要计算出错概率以得到RSSI输出噪声的精确分布。我们相信在给定BER的条件下Eb/No上的误差是很小的,它不会改变下面列出的本文的基本结论。
- 本文描述了RSSI检测器中SNROUT与SNRIN的关系。
- 门限效应。也就是说输入SNR大于3.7dB时输出SNR将有所改善,输入SNR小于3.7dB时输出SNR会变差。
- 灵敏度的改善是与IF带宽和基带带宽之比的平方根成正比的,而不是线性的。
Bales, C. W., "A Comparison of Logarithmic and K-th Law Detectors", IEEE Trans. AES, July 1978, pp. 693-696




















