Accurate and Simple AC Measurement to 500kHz
Introduction
The LTC1967 and LTC1968 provide the easiest way to accurately measure the RMS value of any AC waveform with input signal frequencies as high as 500kHz. They have 1% gain accuracy and noise out to 100kHz and 500kHz, respectively. Their phenomenal linearity of 0.02%, derived from the use of a Delta Sigma architecture, allows easy RMS-to-DC conversion without the need for the calibration that is expected in log-antilog implementations. They also provide much more stable performance over temperature.
Figure 1 shows how easy it is to use the LTC1967 or LTC1968. Each requires only one averaging capacitor and one supply bypass capacitor. The input can be driven differentially or single ended, AC or DC coupled, with a common mode range anywhere between GND and V+. The output has a return pin that provides easy level shifting anywhere between GND and V+.
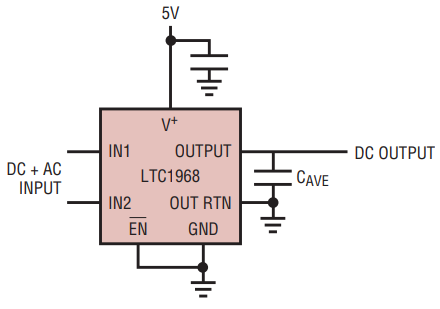
Figure 1. The LTC1967, LTC1968 are easy to hook-up. The only external components are an averaging capacitor and a bypass capacitor.
A designer needs only to select an averaging capacitor big enough to provide the required low and high frequency accuracy, and small enough to meet settling time requirements. That is the only design decision.
Table 1 summarizes the features of the LTC1967 and LTC1968.
| Feature | LTC1967 | LTC1968 |
| Typical Linearity | ±0.02% | ±0.02% |
| Maximum Gain Error | ±0.3% | ±0.3% |
| Bandwidth to 0.1% Additional Error | 40kHz | 150kHz |
| Bandwidth to 1% Additional Error | 100kHz | 500kHz |
| Input/Output Common Mode Range | Rail-to-Rail | Rail-to-Rail |
| Supply Voltage | 5V ±0.5V | 5V ±0.5V |
| Supply Current | 330µA | 2.3mA |
| Package | 8-lead MSOP | 8-lead MSOP |
Advantages of the ∆Σ Topology
The ∆Σ topology used in the LTC1967 and LTC1968 has several advantages. First, the linearity of the RMS-to-DC conversion is unsurpassed. Figure 2 shows the output error versus input. Linearity is typically better than 0.02%. This linearity comes from the fact that the multiplication and division performed using the modulator operates at only two gains: –1 and 1.
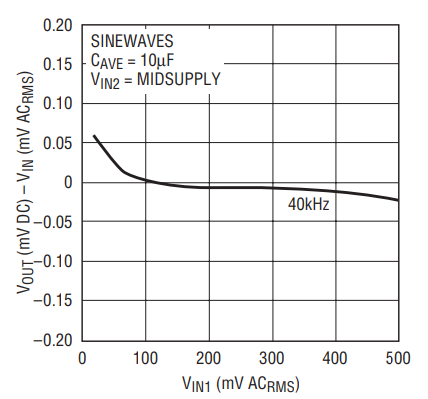
Figure 2. Linearity is typically better than 0.02%.
A second advantage from this architecture is that not much changes over temperature. For example, the gain drifts less than 10ppm/°C. This is an order of magnitude better then converters made using older log-antilog implementations.
The bandwidth and response time of the LTC1967 and LTC1968 is independent of the input amplitude being converted. This again is in contrast to older implementations which have their bias linked to the input amplitude, and therefore slow down with smaller inputs.
Finally, the switched capacitor architecture makes it easy to get rail-to-rail operation at the input and the output. Level shifting the output is as easy as tying the OUT RTN pin to the desired output level.
Selecting the Averaging Capacitor
The only external component that requires careful selection is the averaging capacitor. There are three considerations when selecting the averaging capacitor:
- The accuracy of the conversion at low input frequencies,
- The noise at high input frequencies, and
- The settling time required.
There are two errors at low frequency to consider. One is the DC error in the output and the second is the AC ripple in the output. In the data sheet are curves that show these two errors versus frequency for different values of the averaging capacitor. The larger the averaging capacitor, the smaller both of these errors become.
At higher input frequencies, the noise in the DC output increases because the noise increases with frequency in the ∆Σ modulator. This noise aliases to low frequencies in the DC output. The increased averaging from a larger averaging capacitor lowers this noise. Figure 3 shows the output noise versus input frequency for the LTC1967 and LTC1968. The LTC1968 has lower noise than the LTC1967 at higher frequencies.
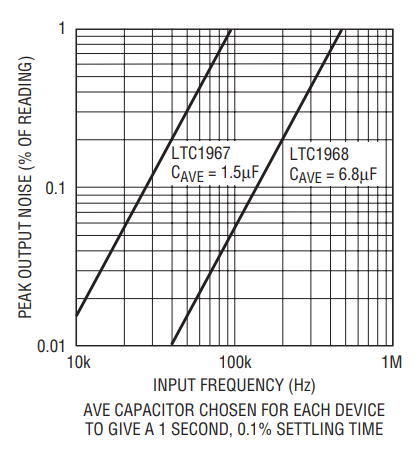
Figure 3. Output noise vs input frequency.
Finally, one must consider the settling time of the device. With larger averaging capacitors, the settling time increases. Since accuracy at low and high frequencies both increase with a larger averaging capacitor, one should use the largest averaging capacitor possible while still meeting settling time requirements. The data sheet has a graph of the settling time versus averaging capacitor.
Conclusion
The LTC1967 and LTC1968 simplify AC measurement by providing calibration-free accuracy, flexible input/output connections, and temperature stability. They maintain their accuracy over a large input frequency range. Both are available in a tiny 8-pin MSOP package.




















