要約
This article investigates the basic theory of software-based receivers for L1-band civilian GPS applications, including a discussion of signal acquisition and tracking, and the need for bit synchronization in the receiver. Also included is a brief description of an L1-band GPS receiver, the MAX2741, which serves as a compact and inexpensive RF front-end for the receiver.
A similar article appeared in the December 2006 issue of Microwaves & RF magazine.
Software techniques for use in the global positioning system (GPS)1, 2 have recently captured the growing interest of communication and navigation engineers. Thanks to VLSI development, powerful CPUs and DSPs are now capable of detecting and decoding GPS signals in real time using software. The resulting software-based GPS receivers offer considerable flexibility in modifying settings to accommodate new applications without hardware redesign, using the same board design for different frequency plans, and implementing future upgrades. This article concentrates on CDMA-communication aspects of the basic theory for software GPS receivers. For the decoding of navigation messages and position calculations, the interested reader can refer to James Bao-Yen Tsui's book, Fundamentals of Global Positioning System Receivers: A Software Approach.3
A GPS system consists of 24 space satellites or space vehicles (each identified by a unique PRN code), a ground-control station, and user equipment (receivers). For civilian GPS applications, the satellites communicate over the L1 band located at 1.57542GHz.
A GPS receiver requires line-of-sight "visibility" of at least four satellites to establish a reliable position. Acquisition and tracking of the signals is very complex, because each one varies with time as well as receiver location. The RF front-end of a software-based GPS receiver (Figure 1) first amplifies the weak incoming signal with a low-noise amplifier (LNA), and then downconverts the signal to a low intermediate frequency (IF) of approximately 4MHz. This downconversion is accomplished by mixing the input RF signal with the local oscillator signal using one or two mixers. The resulting analog IF signal is converted to a digital IF signal by the analog-to-digital converter (ADC).

Figure 1. Simplified diagram of a software GPS receiver.
Analog has integrated this hardware (LNA, mixer, and ADC) in the MAX2741, thus significantly reducing the development time for applications. Its two-stage receiver amplifies the incident 1575.42MHz GPS signal, downconverts it to a first IF of 37.38MHz, further amplifies it, and then downconverts to a second IF of 3.78MHz. An internal 2- or 3-bit ADC (selectable as a 1-bit sign with a 1- or 2-bit magnitude) samples the second IF and outputs a digitized signal to the baseband processor. The integrated frequency synthesizer enables flexible frequency planning, allowing the same board to implement many popular reference frequencies between 2MHz and 26MHz with just a change of settings. The integrated reference oscillator enables operation with either a crystal or a temperature-compensated crystal oscillator (TCXO).
Traditional GPS receivers implement acquisition, tracking, and bit-synchronization operations in an ASIC, but a software GPS receiver provides flexibility by implementing those blocks in software rather than hardware. By simplifying the hardware architecture, software makes the receiver smaller, cheaper, and more power-efficient. You can write the software in C/C++, MATLAB®, and other languages, and port it into all operating systems (embedded OS, PC, Linux, and DSP platforms). Thus, software GPS receivers offer the greatest flexibility for mobile handsets, PDAs, and similar applications.
GPS Signal
We are considering only the civilian GPS signal on the well-known L1 band located at 1.57542GHz. The GPS system is actually a simple spread-spectrum communication system.4 The signal generation block for civilian applications is shown in Figure 2. First, the 50bps navigation message is repeated 20 times to produce a 1000bps bit stream. The repeated signal is then spread by a unique C/A code with a length of 1023 chips (a chip is the rate at which the pseudorandom noise code is applied). The result is a baseband signal of 1.023 megabits per second (Mbps). Hence, the 43dB processing gain (G) of the GPS system permits it to resolve a signal well below the thermal noise level.

Figure 2. Structure of the civilian GPS signal.
Each satellite is assigned a unique C/A code, also called a gold code.5 Because the gold code exhibits excellent auto- and cross-correlation properties, it is widely used in CDMA communication systems such as WCDMA, cdma2000®, and others. The baseband signal is modulated with binary phase-shift keying (BPSK), and upconverted to the L1 band for transmission.
Acquisition
Because GPS is a CDMA communications system, the receiver must synchronize the pseudorandom noise (PRN) code as a prerequisite to demodulating the data. Code synchronization is usually achieved in two steps: code acquisition for the coarse-code alignment, and code-phase tracking for the fine alignment.6
More explicitly, a GPS receiver must first determine whether it has line-of-sight visibility to certain satellites or not. As we know, each satellite is distinguished by a unique C/A code. When the satellite is visible, acquisition determines the signal's frequency and code phase, which in turn establishes the corresponding demodulation parameters. The received-signal frequency varies due to the Doppler effect7, which causes the frequency to deviate from its nominal value by 5kHz to 10kHz, depending on the speed of the satellite with respect to the receiver.
The purpose of signal acquisition is to coarsely determine the carrier frequency and also the C/A code phase, which denotes the start of the C/A code in the data block. Common methods of acquisition include the serial search, which is ideal for hardware implementation due to its simple logic architecture, and frequency-domain parallel code-phase acquisition, whose low computation complexity makes it suitable for software implementation.
A block diagram of the serial-search mode (Figure 3) shows that the received signal is first downconverted to in-phase and quadrature (I and Q) components. A pair of I-Q correlators then correlate the I and Q baseband signals with the locally generated PRN sequence. After integrating over the duration of one bit, the I-Q correlator outputs are summed to provide an output-decision variable.

Figure 3. Serial-search acquisition in the time domain.
Whenever the decision variable exceeds a certain threshold value, the system assumes the corresponding acquisition was successful and proceeds to the tracking mode. Otherwise, the relative phase of the locally generated PRN sequence and the oscillator frequency are adjusted to update the decision variable, and the above process is repeated. The simple logic structure of the serial-search method makes it feasible for implementation in an ASIC, but for software implementations it is not practical because the search space is huge. Assuming the system tolerates a 500Hz carrier-frequency offset and the Doppler frequency is 10kHz, the search space for a software implementation is roughly 2 × (10000/500) × 1023 = 40,920. Obviously, a serial-search acquisition would be difficult in software.
Another acquisition method, called frequency-domain parallel code-phase acquisition, exhibits low complexity in a software implementation (Figure 4). The basic philosophy is to combine the Doppler-frequency and code-phase searches into one, which, after an FFT transform of the PRN code, reflects all code-phase information into the frequency domain. We then need only to search the space over the Doppler-frequency offset, thereby implementing a fast and effective software search.
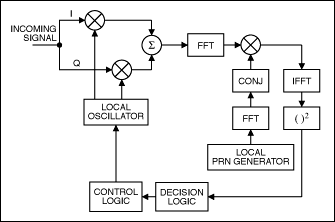
Figure 4. Parallel-search acquisition in the frequency domain.
First, the incoming signal is multiplied with the locally generated sine and cosine carrier waves respectively (the I and Q signal components). The I and Q components are then combined as a complex input to an FFT block. The result of this Fourier transform is multiplied with the conjugate of a PRN code's FFT transform (the PRN generator generates a code with zero-code phase). In practice, the FFT operation and generation of PRN code can be tabulated to reduce computation complexity.
Finally, the product of the incoming signal and local code, which represents the correction between the incoming and carrier frequencies, is applied to an inverse Fourier transform whose squared output feeds back to the decision logic. The FFT-based frequency domain has proven to be a low consumer of computation. For the example mentioned earlier, the complexity of acquisition is roughly 20000/500 = 40 FFT operations. Figure 5 illustrates an FFT-based parallel-code acquisition for the cases of visible (a) and invisible (b) satellites.


Figure 5. Correlator output for FFT-based parallel code acquisition when the satellite is visible (a) and invisible (b).
Thus, the serial-search method has the simple logic and control architecture necessary for a convenient ASIC implementation. The huge search space, however, imposes complexity on the software algorithm. The serial-search method is therefore not a good choice for software GPS receivers. In contrast, the low complexity of the parallel-code acquisition method makes it ideal for the software implementation. Its logic architecture, however, is far more complex than that of the serial-search method, making it difficult to implement in an ASIC.
Tracking
Acquisition establishes a coarse alignment of the GPS signal's frequency and code-phase parameters. The purpose of tracking, therefore, is to refine this alignment so the system can demodulate the data with exact code-phase and frequency information. Tracking includes code-phase tracking and carrier-frequency tracking. Code tracking is accomplished with the delay-lock loop (DLL) shown in Figure 6.

Figure 6. Code-phase tracking technique.
The DLL circuit multiplies the incoming signal by three local replicas of the PRN code (positioned in time at ±0.5 chip), which represent early, prompt, and late arrivals with respect to the incoming signal. After integration, each of these signals represents a correlation between the incoming signal and a local replica. The one with the highest correlation value is then selected and retained (Figure 7). Carrier-frequency tracking is carried out by a phase-lock loop (PLL) or Costas loop.8 The purpose of carrier tracking is to tune the locally generated frequency to the exact frequency of the incoming signal.

Figure 7. These waveforms illustrate operation of the Figure 6 circuit.
Demodulation and Bit Synchronization
After acquisition and tracking have established the initial synchronization, it becomes possible to decode the navigation bits. Data demodulation begins by despreading the 1.023Mbps input signal to a 1000bps bit stream. Bit synchronization is then invoked to recover the 50bps information from the 1000bps stream.
For bit synchronization, we first need to identify the beginning of a bit in time. This is accomplished by finding the zero-crossing edge (at 0V), which indicates the beginning of a bit. When that edge is known, we can partition the 1000bps input stream at 20ms intervals, knowing that the duration of a navigation data message (50 bits) is 20ms (Figure 8). Finally, the bit samples in a 20ms interval are summed and averaged to decode the navigation data.
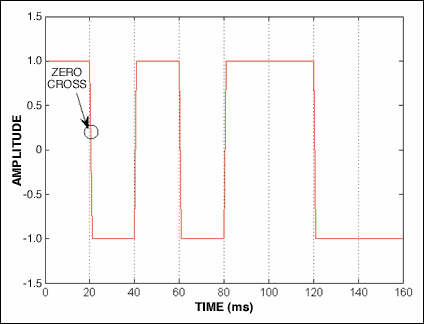
Figure 8. Method of registration for bit synchronization.
Conclusion
This article has briefly introduced certain topics regarding software GPS receivers, including the GPS signal structure, acquisition, tracking, and bit synchronization. Software GPS techniques provide a high level of flexibility and simplicity for many potential applications. To support these possibilities, the MAX2741 compact, inexpensive RF front-end provides flexibility in frequency planning for software GPS receivers and traditional hardware implementations as well. Of course, every solution has its pros and cons—software GPS receivers require a high-performance processor and moderate amounts of memory.




















