要約
This application note starts by explaining Faraday's Law. The note then shows how a voltmeter and connecting wires serve as a positional sensor. A rail-to-rail I/O comparator and a few simple components form an amplitude detector that compares the sinewave amplitude with a DC voltage. The MAX985 rail-to-rail I/O op amp is featured in the design.
Consider two resistors R1 (1kΩ) and R2 (3kΩ), connected in parallel as shown in Figure 1. A time-varying magnetic field H, increasing linearly with time, induces a constant 1mA in the loop according to Faraday's Law. What is the voltage across nodes A-B? According to Ohm's Law the voltages across the two resistors should be different, but how can they differ if both resistors are connected to the same nodes A and B?
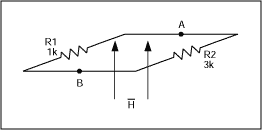
Figure 1. If a time-varying magnetic field H induces a constant current in the loop, what is the voltage between nodes A and B?
The answer may surprise you. The measured voltage depends on the position of wires connecting it to the voltmeter! If two identical voltmeters are connected across nodes A-B as in Figure 2, the simultaneous measured voltages will be -1V and +3V.

Figure 2. Two identical voltmeters measure different voltages across nodes A and B.
The measured voltage is governed by Faraday's Law as explained in a paper by professor Romer[1]. The voltage is defined as the line integral of electric field from node A to B along a path C (Equation 1). The induced electric field in our example is non-conservative, because the closed-loop integral of the electric field is non-zero (Equation 2). Thus, the voltage in Equation 1 is path dependent (in our example).
Integrating the electric field from node A to B along path C1 (Figure 2) gives a value different from that obtained by integrating along path C2. Thus, the measured voltage depends on which path the voltmeter "sees." Another way to understand this action is to consider current in the loop, which is 1mA through both resistors. A given voltmeter sees a voltage drop across either the 1kΩ or the 3kΩ resistor.

To observe this phenomenon, set up an experiment as shown in Figure 3. The magnetic field is produced by a ferrite-core inductor (solenoid) driven by a sinewave. The solenoid size, sinewave amplitude and frequency, and resistor values are not critical, but the resulting induced voltage must be large enough for measurement.

Figure 3. This experimental setup demonstrates operation of the position sensor, which consists of a simple amplitude detector.
Using a 2-channel oscilloscope, measure the voltages simultaneously with a probe across R1 from the left and a second probe across R2 from the right. As expected for the values shown, the sinewave amplitude induced across the 3kΩ resistor is three times larger than that across the 1kΩ resistor, and of opposite polarity (Figure 4).

Figure 4. The amplitude of the top trace (measured across R2 in Figure 3) is about three times larger and of opposite polarity to that of the bottom trace (measured across R1).
Because the value of measured voltage depends on how it is being measured, you can arrange the voltmeter and its connecting wires to serve as a position sensor. Unlike optical position sensors whose narrow sensing field requires a precise initial position to insure detection, the sensor of Figure 3 requires only that the detector be anywhere in the left (or right) hemisphere.
U1 and associated components form a simple amplitude detector that compares the sinewave amplitude with a dc voltage generated by the divider R3/R4. When sensing on the left (1kΩ), the amplitude is too small to turn on the comparator, so its output is logic low. When sensing on the right (3kΩ), the amplitude is large enough to cause oscillation at the comparator output. That signal is rectified to produce a logic high output.




















