MEMS ジャイロ・センサーのクリティカルなノイズ源の予期と管理
モーション・コントロール・システムで MEMS 慣性測定ユニット(IMU)がフィードバック・センサーとして動作している場合、ジャイロ・センサーのノイズは、監視しているプラットフォームで好ましくない物理的な動きの発生源となるため、この挙動を理解するのが重要です。条件によっては、特定の MEMS IMU のアプリケーションを対象にした初期ノイズ見積もりを行う際に、いくつかの潜在的な誤差源を考慮する必要があります。このプロセスで考慮すべき3 つの一般的なジャイロ・センサーの属性は、内在ノイズ、リニア振動への応答、および芯ずれ誤差です。図 1 に、各誤差源の評価に影響を与えるいくつかの属性(ノイズ源、センサーの応答、およびフィルタリング)の単純なモデルを示します。このモデルは、これらの各属性のスペクトル解析のベースラインを提供します。

図 1. ジャイロ・センサーのノイズ源とシグナル・チェーン。
内在センサー・ノイズ
内在センサー・ノイズとは、ジャイロ・センサーが静的な慣性条件や環境条件の下で動作しているときの出力のランダムな変動のことです。MEMS IMU のデータシートには、通常、ジャイロ・センサーの内在ノイズを表す、周波数に対する速度ノイズ密度(RND)パラメータが記載されています。通常、このパラメータの単位は、°/sec/ √Hzで、特定のフィルタ構成の内在ノイズを予測するのに重要な値です。式 1 を使用して、特定の周波数応答(ノイズ帯域幅)と RND でのノイズを簡単に見積もることができます。

RND の周波数応答が単極または 2 極のローパス・フィルタ・プロファイルに追従する場合、ノイズ帯域幅(fNBW)とフィルタのカットオフ周波数(fC)の関係は式 2 と式 3 のようになります。
![]()
![]()
MEMS IMU のデータシートには、RND パラメータに加え、出力ノイズなどのパラメータを使用して、特定のフィルタ構成に対応するジャイロ・センサーの内在ノイズが示されていることもあります。このパラメータは、通常、角速度の標準単位(°/sec)と二乗平均平方根(rms)などの統計値を使用して合計ノイズの大きさを表します。
リニア振動
ジャイロ・センサーは回転の角速度を測定するため、リニア・モーションに対する応答が原因で測定値に誤差が生じます。MEMS IMUのデータシートでは、通常、このリニア・モーションに対する応答をバイアスに対するリニア加速度の影響またはリニア-g(単位は °/sec/g)などのパラメータで表しています。リニア振動は反復慣性運動で、振幅は変位(m)、線速度(m/s)、または線加速度(m/s2 または g)に関係します。特定の振動周波数(fLV)で、変位(|dLV|)、速度(|vLV|)、および加速度(|aLV|)の大きさは式 4 に従って相互に関係します。
![]()
振幅が加速度(grms)に関係する場合、その値にリニア-g パラメータを乗算してジャイロ・センサーの測定値のノイズを見積もります。例えば、ADIS16488A で 5 g(rms)の振動が発生する場合、リニア-g は 0.009 °/sec/g であるため、ジャイロ・センサーのノイズは 0.045°/sec(rms)になります。

図 1 に示しているように、ジャイロ・センサーのシグナル・チェーンには、通常、リニア振動によるノイズ成分を軽減するためのフィルタが含まれています。振動をスペクトル(振幅、周波数)で定義することで、ノイズ成分を見積もる際にフィルタの効果を考慮できます。加速スペクトル密度(ASD)関数はスペクトルで振動を表す一般的な方法で、単位は g2/Hz です。次のステップでは、ASD とジャイロ・センサーの周波数応答(HG)が既知の場合に、ノイズの大きさを見積もる手順を示します。
1. ASD 関数に、ジャイロ・センサーの周波数応答を二乗した値を乗算します。
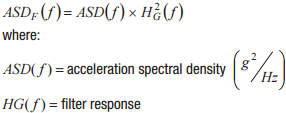
2. パーセバルの定理を使用して、ASDF を対象周波数範囲で積分し、「フィルタリングされた振動プロファイル」の平均パワーを計算します。

3. ノイズ・パワーの見積もり値の平方根にリニア-g 係数(HLG)を乗算して、ジャイロ・センサーのノイズの大きさを計算します。
![]()
芯ずれ誤差
モーション・コントロール・システムでは、通常、互いに 90° を成す 3 つの軸で構成された慣性座標系を定めます。これら 3 つの軸は、MEMS IMU 内の各センサーの方向の基準となります。理論的には、各ジャイロ・センサーの回転軸は、動作時に監視対象のプラットフォームに IMU を設置した後に、システムの座標系と完全に一致するようになります。この場合、慣性座標系の 1 つの軸を中心とした回転は、その軸のジャイロ・センサーのみに関する応答を生成します。実際には、この応答は実現不可能です。機械的な不完全性により、何らかの芯ずれ誤差が必ず発生し、軸外のジャイロ・センサーが慣性座標系の 1 つの軸を中心とした回転運動に応答するようになるからです。この応答を定量化するには、三角恒等式を使用してジャイロ・センサーの芯ずれ誤差を注意深く定義する必要があります。
各ジャイロ・センサーの芯ずれ誤差には 2 つの成分があり、それぞれが慣性座標系の他の軸に対する芯ずれ誤差を定義します。例えば、図 2 の座標系で、θXZ は、Z 軸に対する X 軸ジャイロ・センサーの芯ずれ誤差を表しています。この芯ずれ誤差の定義は、システムの慣性座標系の他の軸を中心とした回転に対する軸外ジャイロ・センサーの応答を計算するための式を作成する際に役立ちます。式 9 は、Z 軸に関する芯ずれ(θXZ)と Z 軸を中心とした回転(ωZR)による X 軸ジャイロ・センサーの応答(ωGX)を定量化します。

図 2. 3 軸ジャイロ・センサーの芯ずれ誤差。
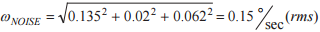
MEMS IMU には、通常、「軸/パッケージ」と「軸/軸」の 2 種類のアライメント誤差があります。これらは互いに関連していますが、システムレベルのモデリングの異なる用途で使用します。「軸/パッケージ」の芯ずれ誤差は、デバイス・パッケージの特定の機械的特性に関するジャイロ・センサーのアライメントを表します。IMU をシステムに設置した後に、システムが慣性アライメントをサポートできない場合、「軸/パッケージ」の芯ずれ誤差は全体的な芯ずれ誤差の最大要因の 1 つとなります。IMU に対するシステムの機械的な接合面の機械的な不完全性も、全体的なアライメント誤差の要因となります。「軸/軸」の芯ずれ誤差は、各ジャイロ・センサーの回転軸について、他の 2 つのジャイロ・センサーに関する相対的なアライメント精度を表します。システムが単純なアライメント・プロセスを実装できる場合、このパラメータは最も強い影響を及ぼします。これには、システムの慣性座標系の 1 つの軸に沿ってアセンブリ全体(IMU がシステム・プラットフォームに設置された状態)を直線的に動かしたときのセンサーの監視が含まれます。
芯ずれ誤差が IMU の仕様に含まれていない場合、デバイス・パッケージの主要な機械的特性の物理的な許容値を評価することで、これらの誤差を見積もれることがあります。例えば、次の場合に0.5° の芯ずれ誤差が発生します。
- 4 mm × 4 mm LGA パッケージのリフローはんだ付けでの 35 μm のセトリング誤差
- PCB 上における 20 mm 間隔の 2 つの取り付け穴の 0.175 mm の許容差
ケース・スタディ
これらの原理を説明するため、次の例を取り上げます。ここでは、次の構成/条件で動作する新しいアビオニクス・システムのADIS16488A でのジャイロ・センサーのノイズを見積もります。
- ジャイロ・センサーから全帯域幅を利用可能
- 振動(ASD(f)):0.122 g2/Hz、10 Hz ~ 2000 Hz(合計振動 = 5 grms)
- 最大回転速度 = ±100°/sec、周波数範囲 = 5 Hz ~ 50 Hz
全帯域幅の構成は、ADIS16488A の内在センサー・ノイズの出力ノイズ仕様である 0.135°/sec(rms)に関連付けられた条件に一致します。振動成分については、図 3 にプロファイル ASD(f) とフィルタリングされたプロファイル ASDF(f) を示します。ASDF(f) の周波数応答は、この IMU のジャイロ・センサーの信号経路の 2 極(404 Hz、757 Hz)ローパス・フィルタに関連付けられた減衰プロファイルを反映しています。

図 3. 振動スペクトル解析。
式 10 では、ASDF(f) プロファイルの大きさである 2.24 grms をリニア-g パラメータで乗算して、結果のノイズ・レベルである 0.02°/sec(rms)を見積もっています。このノイズ・レベルは、スペクトルに関してこのノイズ源を評価しなかった式 5 で得られた0.045°/sec(rms)レベルよりも 55 % 低い値です。この改善は、スペクトル項で振動プロファイルを定義することによって得られた値の 1 つの例です。
![]()
式 11 は、50Hz の周波数で、z軸周りに ±100°/ sec の回転振動から来る x 軸ジャイロ・センサーのノイズの計算を提供します。 50Hz は 2 極フィルタの通過帯域内にあるため、フィルタはこのノイズ源を除去しません。 この計算では、ADIS16488A の軸間の芯ずれ誤差が芯ずれ誤差の主な原因になると想定しています(言い換えると、IMUをシステムにインストールした後、完全な配備には単純な慣性フレーム・アライメント・プロセスが含まれます)。

表 1 に、ADIS16488A の各属性によるジャイロ・センサー・ノイズを示します。式 12 で全体的なノイズの見積もり(ωNOISE)である0.15°/sec(rms)が得られています。これは表 1 に示す 3 つのすべてのノイズ源の二乗和平方根(RSS)です。
| 成分 | ノイズ (°/sec) |
| 内在センサー・ノイズ | 0.135 |
| リニア振動応答 | 0.02 |
| 芯ずれ |
0.088 |
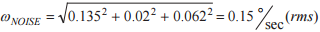
結論
これらのテクニックは、データシートに記載されている一般的なパラメータ情報や、慣性条件の予備的な情報や見積もりを使用して、MEMS ジャイロ・センサー信号の一般的なノイズ源を評価するための簡単なプロセスを提供します。これらのノイズ源を理解および評価することで、重要なアプリケーション情報を特定したり、IMU 選択プロセスでの指針としたり、別の方法による経済的なソリューションを実現する優れた方法(IMU が適切な「軸/軸」の芯ずれ誤差レベルをサポートしている場合に簡単なアライメント)を見出すことができます。




















