RF回路のインピーダンス・マッチング、必要な計算方法とシミュレーション方法を学ぶ
概要
本稿では、まず、RF回路におけるインピーダンス・マッチングの基本について説明します。その上で、マッチングを実現するための部品の値の計算方法、LTspice®による結果の確認方法について解説します。
はじめに
電子回路の理論によれば、ソースの抵抗と負荷の抵抗の値が一致している場合に、ソースから負荷に対して最大の電力が伝送されます。ただ、ほとんどのRF回路では、ソースと負荷のインピーダンスにリアクタンス成分が含まれています。その場合、最大の電力を伝送するためには、ソースのインピーダンスが負荷のインピーダンスの共役複素数と等しい値になっていなければなりません。つまり、ソースのインピーダンスと負荷のインピーダンスについては、実数部は同一の値で、虚数部は絶対値が同じで符号が逆の状態になっている必要があります。
一般に、RFシステムで使われるパワー・アンプの回路は簡素なものにはなりません。その回路が複雑になってしまう理由は、多くの場合、主要な能動部品であるトランジスタ(IC)の周囲にインピーダンス・マッチングを実現するための部品を追加しなければならないことにあります。実は、回路の残りの部分はそれほど複雑なものではありません。重要なのは、インピーダンス・マッチングを実現するための回路は、どのような計算に基づいて構成するのかを理解することです。マッチング用の部品の値を計算する作業は、決して難易度の高いものではありません。また、計算の内容をクロスチェックするツールがあれば非常に便利です。つまり、ソースから負荷に対して最大の電力が伝送されることを確認するためのツールを利用すべきだということです。
Chris Bowick氏が執筆した「RF Circuit Design」は、多くの技術者がバイブルとして活用している名著です。本稿では、同書で説明されているインピーダンス・マッチングの理論について詳しく説明します。また、計算のクロスチェックを行うためのツールとして、LTspiceを利用する方法も紹介します。インピーダンス・マッチングを実現するための回路の全体像を把握するために、ぜひ「RF Circuit Design」をご一読ください。その際には、本稿で説明する内容が理解の助けとなるはずです。
共振回路と負荷Q
コンデンサのリアクタンスは、次式で与えられます。

この式の分子と分母にjをかけると、コンデンサのリアクタンスは負の値であることがわかります。一方、インダクタのリアクタンスは、以下の式で与えられるように正の値になります。

ある周波数において、値が等しく符号が逆のリアクタンスを備えるコンデンサとインダクタを直列に接続したとします。その場合、位相シフトがゼロのショート・サーキットが形成されることになります。同様に、それらの部品を並列に接続すると、位相シフトがゼロのオープン・サーキットが形成されます。一般に、並列に接続された2つの部品のインピーダンスは、2つのインピーダンスの積を、2つのインピーダンスの和で割ることによって求められます。2つの部品のリアクタンスの値が等しく符号が逆である場合には、分母がゼロになってオープン・サーキットが形成されることになります。
ここで、リアクタンス成分に抵抗を並列または直列に接続したものが負荷であるケースを考えます。その負荷Qの値は、リアクタンスと抵抗の比として求められます。並列に接続した場合のQの値は、次式で定義されます。

一方、直列に接続した場合のQの値は次式で定義されます。

ここで、RpとRsはそれぞれ並列抵抗と直列抵抗の値、XpとXsはそれぞれ並列リアクタンスと直列リアクタンスの値です。
回路網の負荷Qに基づいた計算を行えば、並列回路網を直列回路網に変換することができます。そうすると、マッチングの作業が大幅に簡素化されます。直列等価回路を導出したら、インピーダンス・マッチングは、実数成分が等しく虚数成分の符号が逆のソース・インピーダンスを選ぶだけで実現できるからです。
図1に示す回路のインピーダンスは、次式で与えられます。

ここで、-jXcpは、並列接続したコンデンサのリアクタンスです。

図1. 抵抗とコンデンサを並列に接続した回路網
この回路の直列等価回路は、いくつかの方法によって得ることができます。式(5)の分子と分母に分母の共役複素数をかけると、直列回路の実数部と虚数部の値を求められます。あるいは、この式を極形式に変換し、直列部品の実数部と虚数部を正弦関数と余弦関数を使用して計算することも可能です。
直列部品をより迅速に求めるには、まず式(3)を使用して並列回路網の負荷Q(Qp)の値を求めます。そして、得られた値を次式に代入します。

これにより、新たな直列抵抗の値が求められます。次に、Qの値が等しい直列回路網を設計します。そして、新たな直列抵抗Rsの値を式(4)に代入し、新たな直列リアクタンスXsの値を求めます。なお、式(6)の導出方法については、稿末の付録をご覧ください。
図1の回路の場合、負荷Qの値は10になります。これは、並列抵抗を並列リアクタンスで割ることによって求められます。式(6)を使用すれば、1kΩの並列抵抗を9.9Ωの直列抵抗Rsに変換することができます。また式(4)からは、直列コンデンサのリアクタンスは-j99Ωでなければならないことがわかります。このようにすれば、特定の周波数において、図1の回路は図2の回路と同一のインピーダンスを示すようになります。

図2. 図1の回路の直列表現
図2の負荷を見ると、実数部が9.9Ω、虚数部が負の値(-j99Ω)になっています。したがって、最大の電力の伝送を確実に達成するには、実数部が9.9Ωで虚数部が正(j99Ω)のソース・インピーダンスが必要になります。負荷のリアクタンスと値が等しく符号が逆のソース・リアクタンスを選択すれば、2つのリアクタンスが相殺されます(ショート・サーキットを形成)。その結果、ソース抵抗によって、それと値の等しい負荷抵抗を駆動する状態になります。
ここで、図2の直列回路は、図1と等価な回路を示したものに過ぎません。つまり、図1の構成に変更を加える必要はありません。図1の並列回路を、直列インピーダンスが(9.9 + j99)Ωのソースで駆動する場合に、最大の電力が伝送されることになります。
重要なのは、並列回路のリアクタンス(図1のCp)によって、回路のQの値で決まる係数を基に、1kΩの抵抗より値の小さい等価な直列抵抗が生成されるということです。直列回路のコンデンサやインダクタのリアクタンスについても同様のことが言えます。直列RC回路(図2)では、直列のリアクタンス(コンデンサかインダクタかは問わない)によって、直列抵抗Rsと等価な並列抵抗の値は大きくなります。ここで、式(6)を以下のように変形してみましょう。

これを見れば、並列抵抗は直列抵抗の(Q2 + 1)倍になることは明らかです。
ここまでに述べた内容から、次のようなことがわかります。すなわち、並列/直列のリアクタンスを使用すれば、抵抗値を小さく見せたり、大きく見せたりすることが可能だということです。並列RC回路網の負荷Qの値は、そのリアクタンスの値に対する抵抗の値の比で決まります。その負荷Qを利用し、まずは並列回路網を直列回路網に変換します。その上で、(直列の)負荷インピーダンスの実数部と等しくなるようにソース・インピーダンスの実数部を選び、なおかつ直列負荷インピーダンスのリアクタンス部と値が等しく符号が逆になるように、ソース・インピーダンスのリアクタンス部を選べばよいということです。
ソースと負荷のインピーダンスが固定の場合の対応
残念ながら、ソースのインピーダンスの値を変更できるケースはめったにありません。通常、ソースと負荷のインピーダンスは、あらかじめ決定されています。したがって、これら2つをマッチングさせるには、そのための回路網(マッチング回路網)を新たに設計する必要があります。

図3. 50Ωのソースに対するマッチング用の回路。100MHzにおいて1kΩの負荷とマッチングさせるために、部品を追加します。
図3の回路をご覧ください。この回路のソース抵抗の値は50Ωです。100MHzにおいて、このソース抵抗と1kΩの負荷をマッチングさせる必要があるケースを考えましょう。その場合、シャント・コンデンサを使用して、1kΩの並列抵抗を50Ωの直列抵抗に変換します。式(6)を基に考えると、そのためには、抵抗とコンデンサを組み合わせた負荷Qの値が4.36になるようにしなければならないことがわかります。それにより、50Ωの等価直列抵抗と、特定の値(後ほど算出)の直列コンデンサが得られます。続いて、直列コンデンサと値が等しく符号が逆のリアクタンスが得られるように直列インダクタの値を選択します。このようにすれば、2つのリアクタンスが相殺され、50Ωの抵抗が50Ωの負荷に接続されているのと同じ状態になります。
式(3)を使用すれば、以下のように並列コンデンサのリアクタンスを計算することができます。

並列コンデンサの値は、100MHzにおいてリアクタンスが-j229Ωになるよう6.94pFに設定します。以上で並列回路網が完成しました。これを直列回路網に変換するには、並列回路網と直列回路網のQが等しくなるようにします。式(4)を使用すると、並列回路は、Rsが50Ωで、次式で求められるリアクタンスを備える直列回路網に変換できます。

上記の式を計算すると、Xsは218Ωになります。
6.94pFのコンデンサと1kΩの負荷を組み合わせた並列回路は、50Ωの直列抵抗とリアクタンスが-j218Ωの直列コンデンサで構成される回路と等価です。リアクタンスがj218Ωになるように直列インダクタを選択すれば、マッチング回路網のリアクタンス部は相殺されます。その結果、50Ωのソースが50Ωの実効負荷抵抗を駆動する状態になります。最終的には、図4に示した回路網が得られます。

図4. インピーダンス・マッチングを実現した回路。50Ωのソースに対し、100MHzにおいて1kΩの負荷がマッチングするように回路を構成しています。
図4の回路については、LTspiceを使用することでシミュレーションによって特性を確認することができます。LTspice上で回路を構成し、抵抗R1とインダクタL1を接続したノードにINというラベルを付けることにしましょう。INノードにプローブを当ててプロットを取得することにより、L1に流れ込む電流を基にしてソースから見た負荷のインピーダンスをプロットすることができます。そのためには、波形ウィンドウにおいてI(L1)の上で右クリックし、テキストをコピーします。次に、V(in)のアイコンを右クリックし、テキストを「V(in)/I(L1)」に変更します。すると、図5に示すように、マッチング回路網の入力インピーダンスがプロットされます。

図5. マッチング回路網の入力インピーダンス
図5のプロットにおいて、インピーダンスはdB単位で表示されています。左右のy軸によって実数成分、虚数成分が表示されるように変更するには、左側のy軸上で右クリックします。それによって表示されるボックスにおいて、「Representation」のメニューを開き、「Bode」から「Cartesian」への変更を行います(図6)。

図6. y軸の設定の変更。BodeからCartesianに変更しています。
図7に示したのが、最終的に得られるプロットです。ご覧のように、左のy軸は実数成分、右のy軸は虚数成分に対応しています。カーソルを100MHzの位置に置くと、図4の回路網のインピーダンスは確かに50Ωであり、虚数成分は極めて小さくなっていることがわかります。

図7. 最終的なプロット。100MHzにおいて、インピーダンスは50 + j0Ωに近い値になり、マッチングが実現されていることがわかります。
波形ウィンドウを閉じてシミュレーションを再実行した場合、V(in)とI(L1)を再度プローブし、一方を他方で割って、y軸の設定をデカルト座標に設定しなおす必要があります。この面倒な作業は、波形ウィンドウを選択し、「File」メニューから「Save Plot Settings As」を選択することで不要になります。この操作を行うと、現在の波形表示の設定が保存され、シミュレーションを再実行した際にも自動的に同様のプロットを得ることができます。(図8)。

図8. 「Save Plot Settings As」の選択。これにより、y軸の設定とプロットした波形を保存することができます。
Qの値が既知である場合の設計
上記の例では、並列コンデンサを使用し、1kΩの負荷抵抗が50Ωの直列抵抗と任意の直列コンデンサを組み合わせたものに見えるようにしました。その上で、インダクタを使って直列コンデンサのリアクタンスを相殺しました。その結果、図4に示すL型の回路網が得られました。ただ、このマッチング回路網では、Qの値を選択することはできません。Qは、ソースと負荷のインピーダンスによって決まるからです。この点を改善するためには、図9に示すようなT型の回路網を使用するとよいでしょう。この回路は、L型の回路網を2つ用意し、それらをバック・ツー・バックで接続することによって構成しています。
この例では、Qを所望の値に維持しながら、2.1Ωの負荷抵抗が50Ωに見えるようにします。まずは、直列回路から並列回路への変換手法を適用してみます。

図9. 仮想抵抗を備えるT型の回路網
L型の回路網では、直列インダクタを使用して直列コンデンサのリアクタンスを相殺しました(ショート・サーキットを形成)。一方、T型の回路網では、並列インダクタを使用して並列コンデンサのリアクタンスを相殺します(オープン・サーキットを形成)。
図9では、直列インピーダンスXS2(コンデンサまたはインダクタ)によって、2.1Ωの直列負荷抵抗を、より大きな等価並列抵抗と任意の並列リアクタンスを加算したものに変換しています。任意の並列リアクタンスと値が等しく符号が逆になるようにXP2を選択することで、オープン・サーキットを形成することができます。その結果、2.1Ωの抵抗が、リアクタンス成分を持たない、はるかに大きな並列抵抗Rvのように見えるようになります。
図中の抵抗Rvは、実際に回路に配置されているわけではないので注意してください。Rvの位置から見た場合に、抵抗の値が2.1Ωより大きく見えるようにしただけです。実際、この回路については、2.1Ωの抵抗、XS2、XP2をRvに置き換えて簡略化することができます。そして、その回路をソースから見た場合、特定の周波数で同一のインピーダンスが得られている状態になります。
ここで、式(6)を次式のように変形します。

仮想抵抗の値が50Ωのソース抵抗と比べて大きいほど、回路のQが大きくなることがわかります。このように、Rvが任意の値に見えるようにXS2とXP2を変更することによって、所望のQの値を得ることができます。L型の回路網を使用すれば、ソース・インピーダンス(50Ω)を負荷抵抗Rvにマッチングさせることが可能です。XP1を使用し、Rvがより値の小さい直列抵抗(理想的には50Ω)と任意の直列リアクタンスを組み合わせたものに見えるようにすると共に、その任意の直列リアクタンスと値が等しく符号が逆になるようにXS1を選択します。その結果、50Ωのソース抵抗が50Ωの負荷抵抗に接続された状態になり、Qが高い値に維持されます。
上記の方法について詳しく検討してみましょう。まず、100MHzにおいて、50Ωのソースが2.1Ωの負荷にマッチングするようにし、回路のQが10という所望の値になるようにします。その目的は、図9の回路が、50Ωのソースとより値の大きい負荷抵抗Rvを備えるL型の回路網のように見えるようにすることです。そのためには、2.1Ωの抵抗を、より値が大きい(並列)抵抗に変換しなければなりません。直列リアクタンスXS2により、2.1Ωの抵抗がより値の大きい並列抵抗に変換されることはわかっています。式(4)から、以下のような結果が得られます。

したがって、XS2は21Ωになります。
次に、以下のように式(6)を使い、この直列回路をそれと等価な並列回路に変換します。

この式から、Rpの値は212.1Ωになります。これが仮想抵抗の値です。
つまり、2.1Ωの直列抵抗と21Ωの直列リアクタンスは、より値が大きい212.1Ωの並列抵抗と任意の並列リアクタンスを組み合わせたもののように見えることになります。続いて、値が等しく符号が逆の並列リアクタンスを挿入してリアクタンスを相殺します。すなわち、オープン・サーキットを形成し、より値の大きい並列抵抗だけが残るようにします。その並列リアクタンスを決定するためには、式(3)を使用します(以下参照)。

この式から、XP2は21.21Ωになります。
必要であれば、XS2、XP2、2.1Ωの抵抗を、値が212.1Ωの単一の並列抵抗に置き換えることができます。その回路の負荷は、100MHzにおいてソースと同一のインピーダンスを示します。この回路についても、LTspiceによるシミュレーションで特性を確認することが可能です。以上のような対応を図れば、この回路は単純なL型の回路網として扱えるようになります。その回路では、50Ωのソース抵抗が212.1Ωの負荷とマッチングしている状態になります。得られた値を式(10)に適用すると、以下のようにQの値が求まります。

212.1Ωの並列抵抗が50Ωの直列抵抗のように見えるようにするにはどうすればよいでしょうか。まず、抵抗とQの値はわかっているので、そのQの値を得るために必要な並列リアクタンスの値を求めます。続いて、Qの値が同一の等価直列回路を作成します。その上で、並列リアクタンスを挿入すると、その値の大きい並列抵抗が、値の小さい直列抵抗(50Ω)と、ある値の直列リアクタンスを組み合わせたものに変換されます。式(3)を使えば、以下のように計算を行うことができます。

これを解くと、XP1の値は117.8Ωになります。
つまり、117.8Ωの並列リアクタンスによって、212.1Ωの並列抵抗が50Ωの直列抵抗のように見えるようになります。続いて、式(4)を使用することにより、直列リアクタンスの値を計算します。
117.8Ωの並列リアクタンスと212.1Ωの並列抵抗によって、Qの値は1.80になります。Qの値が等しく、50Ωの直列抵抗を備える直列回路への変換を行うと、直列リアクタンスの値を計算できます。
式(4)を使用すれば、以下の式が得られます。

これを解くと、XS1の値は90Ωになります。
212.1Ωの並列抵抗と117.8Ωのリアクタンスを組み合わせたものは、50Ωの直列抵抗と90Ωのリアクタンスを組み合わせたもののように見えます。XP1がコンデンサである場合、それは(リアクタンスが-j90Ωの)直列コンデンサに変換されます。このリアクタンスを相殺するために、マッチング用の直列部品としては、(リアクタンスがj90Ωの)インダクタを使用する必要があります。
上記の手順については、いくつか注意すべき点があります。まず、T型の回路網については、回路の末端にある値が最も小さい抵抗(上記の例では、50Ωではなく2.1Ω)から設計を始めます。もし50Ωの側から設計を始めると、式(6)を利用した計算によって求めたRvの値が非常に大きくなります。負荷抵抗の値はそれよりもはるかに小さい2.1Ωなので、回路網の右半分のQの値が非常に大きくなってしまいます。また、直列リアクタンスは、シャント・リアクタンスに対して常に符号が逆でなければならないということにも注意が必要です。両者が確実に相殺し合うようにしなければならないということです。このことから、通常、直列コンデンサに対してはシャント・インダクタを用意する必要があります。その逆についても同様です。
ここで、表1をご覧ください。これは設計に使用した各部品の値をまとめたものです。
| 部品 | インピーダンス | 100MHzにおける値 |
| XS1 | 90 | 17.68pF |
| XP1 | 117.8 | 187.5nH |
| XS2 | 21 | 75.79pF |
| XP2 | 21.21 | 33.76nH |
XP1とXP2は並列インダクタです。したがって、これらは28.61nHの単一のインダクタにまとめることができます。最終的な回路は図10のようになります。

図10. 最終的なT型の回路網
INノードの電圧をC1に流れ込む電流の値で割ると、マッチング回路網の入力インピーダンスを求められます。図11に示したのが、その結果をプロットしたものです。ご覧のように、マッチング回路網の入力インピーダンスは、100MHzにおいて50Ωに非常に近い値になることがわかります。

図11. マッチング回路網の入力インピーダンス。100MHzにおいて、50Ωに非常に近い値になります。
また、負荷にかかる電圧と負荷に流れる電流をかけ合わせれば、負荷に伝送される電力の値が得られます。その結果をプロットすると、図12のようになります。

図12. 電力のプロット。100MHzにおいて最大の電力が伝送されます。
プロットのウィンドウ上で右クリックし、「Add Plot Pane」を選択すれば、1つのウィンドウにインピーダンス、別のウィンドウに電力を同時に表示することができます。また、表示の設定を保存しておけば、シミュレーションを実行するたびに同じ設定の表示を自動的に行うことが可能になります。
より複雑な負荷への対応
負荷が純粋な抵抗性のものであることはほとんどありません。例として、図10の2.1Ωの負荷に398pF(100MHzで-j4.0Ωに相当)の容量性の素子が直列に接続されているケースを考えましょう。その場合、ここまでに設計したマッチング回路網はうまく機能しません。ただ、この問題は簡単に解決することができます。図10では、コンデンサC2と2.1Ωの負荷によって直列回路が形成されています。Qの値は、抵抗(2.1Ω)に対するリアクタンス(-j21Ω)の比から10と求まります。この回路に-j4.0Ωの負荷を追加すると、全体のリアクタンスは-j25Ωに増大します。Qの値を維持するためには、この直列回路に正のリアクタンスを追加し、負荷の値である-j4.0Ωを相殺しなければなりません。これは、6.37nHのインダクタ(リアクタンスはj4.0Ω)をC2に直列に追加し、抵抗に対するリアクタンスの比を維持することで実現できます。より簡単な方法は、容量C2の値を93.62pFに増加させることです。そうすると、リアクタンスが-j17Ωに低下します。ただ、負荷のコンデンサによって正味の直列リアクタンスが増加して-j21Ωまで戻るので、Qの値は10のまま維持されます。最終的な回路は図13のようになります。LTspiceを使用してこの回路のシミュレーションを行えば、マッチングが実現されていることを確認できます。
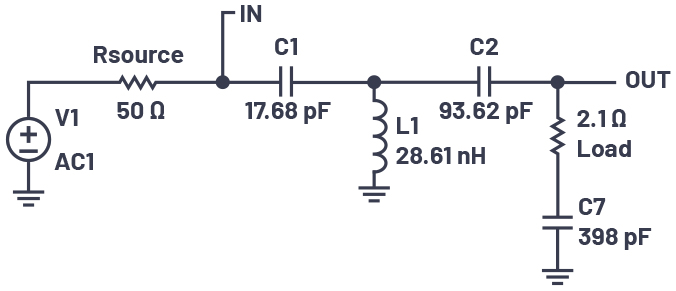
図13. 修正を加えたT型の回路網。より複雑な負荷に対してマッチングするように回路を変更しています。
図14を見ると、この回路は100MHzにおいて50Ωに適切にマッチングしており、最大の電力が伝送されることがわかります。

図14. 図13の回路のシミュレーション結果。より複雑な負荷がある場合でも、100MHzにおいてインピーダンスが適切にマッチングし、出力電力が最大になることがわかります。
まとめ
本稿では、RF回路のインピーダンス・マッチングについて詳しく説明しました。RFに対応するパワー・アンプ回路について、より容易に理解できるようになったはずです。回路網の負荷Qを使用すれば、直列回路網と並列回路網を切り替えて、値の小さい抵抗を値の大きい抵抗に変換することができます。ただ、あらゆる設計作業と同様に、計算結果については常にクロスチェックを行うようにすることが重要です。LTspiceを使用すれば、回路のインピーダンスと電力の値をプロットし、適切な設計が行われていることを確認することができます。