LTspiceでボーデ線図を取得する

概要

動的なシステムを開発する際には、システムの周波数応答を確認したいケースがよくあります。電気工学、制御工学の領域はもちろん、機械工学の領域でも、周波数応答は重要な意味を持つことがあります。周波数応答は、システムに高調波励起（正弦波発振）を入力した場合に、定常状態のシステムの出力がどのようになるかを把握するために取得されます。その際に使用されるのがボーデ線図です。ボーデ線図は、システムの伝達関数から振幅と位相の各応答を求め、それぞれを周波数の関数としてグラフ化したものです。多くの場合、周波数軸については対数目盛が使用されます。通常、振幅応答にはデシベル単位の値（つまりは対数値）が使われます。また、複数の単純なグラフを組み合わせることにより、複雑なボーデ線図を作成することもできます。例えば、伝達関数が複数存在するとして、それらを組み合わせた場合の振幅応答は、各伝達関数の振幅応答（デシベル単位の値）を加算することによって取得することが可能です。位相応答については、対数目盛を使うことなくそのまま加算的に重ね合わせることができます。対数表示には、1つのグラフ上に同じ相対精度でより広い周波数範囲の特性を表示できるというメリットがあります。

LTspiceによる周波数応答の取得

LTspice^®は、アナログ回路用の強力なシミュレーション・ソフトウェアです。これを使えば、時間領域の信号を周波数領域に変換して電気回路の周波数応答を取得することができます。LTspiceはSPICEをベースとしており、多様な電子コンポーネントを扱うことができます。小信号解析やモンテカルロ・シミュレーションを実行することも可能です。

以下、簡単な回路を例にとり、LTspiceを使ってその周波数応答を取得する方法を説明します。回路のシミュレーションを実行し、その結果としてボーデ線図を取得する手順を示します。図1に示したのが、本稿で例にとる回路です。ご覧のように、2次のローパス・フィルタが構成されています。回路の入力ノードと出力ノードには、それぞれ「Input」、「Output」というラベルを付与してあります。これらは、シミュレーション結果を表示する際に役立ちます。

この回路の周波数応答を得るためには、正弦波を入力してシミュレーションを実施することになります。これは、AC掃引の機能を適用することで簡単に実現できます。LTspiceのメニューで「Simulate」→「Edit Simulation Cmd」を順に選択し、「AC Analysis」タブを開いてください。ここで、シミュレーションに使用するパラメータの値を入力します。ボーデ線図のX軸は対数目盛で表示します。「Type of Sweep」では「Decade」を選択してください。必要に応じ、残りのパラメータの値も入力します。

AC解析では、回路に印加する入力電圧を設定する必要があります。電圧源のパラメータに関するメニューにおいて、「Small Signal AC Analysis」を選択してください。ここでは、所望の振幅として1Vを指定することにしましょう。以上で、シミュレーションを実行できる状態になりました。「Simulate」→「Run」を選択し、シミュレーションを実行してみてください。シミュレーションが正常に終了したら、自動的に空のプローブ・エディタが表示されます。ここで回路内の出力ノード（Output）を選択すると、振幅と位相が周波数の関数として表示されます。

システムの周波数応答は、入力信号に対する出力信号の比で求められます。そのため、ここでは表示を少し調整する必要があります。「Expression Editor」で「V(output)/V(input)」という関数を指定してください。その結果、回路の周波数応答として振幅応答と位相応答が正しく表示されます。

図2は、図1の回路の周波数応答を表示した結果です。ご覧のように、2次のローパス・フィルタの特性が周波数の関数として示されています。振幅については、左側のY軸を見ればわかるようにデシベル単位で表示されています。一方、右側のY軸を見ればわかるように、位相（位相シフト）については度（°）を単位として表示されています。

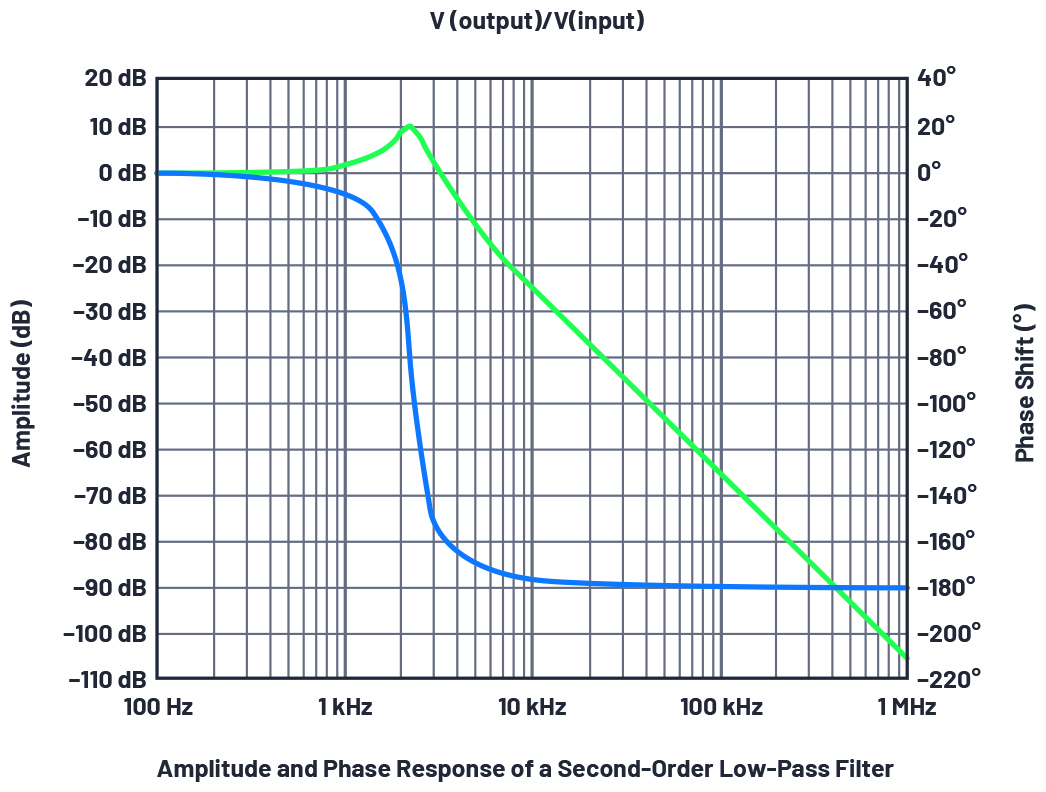
図2. 2次ローパス・フィルタの周波数応答。振幅と位相が周波数の関数としてグラフ化されています。

グラフ上の各点の正確な値を読み取るにはカーソルを追加します。それには、グラフに表示されている波形のノード名をクリックしてください。ダブルクリックするとカーソルが2つ表示され、各カーソル位置の絶対値と、2つのカーソル位置の値の差が別のウィンドウに表示されます。

まとめ

本稿で説明したように、LTspiceによるシミュレーションを実行すれば、回路の周波数応答を簡単に取得することができます。LTspiceでは、標準的なボーデ線図は周波数（f）の関数として表示されます。本稿では説明を割愛しましたが、表示方法に変更を加えることにより、角周波数（ω）の関数としてボーデ線図を表示することも可能です。