要約
This application note describes a compact 5W flyback, high-frequency, switching converter for Telecom applications. Most aspects of the design process are discussed: power-stage selection and design, transformer design, core size calculations, RCD snubber design, MOSFET selection, input and output filter designs, frequency compensation, power-loss and efficiency calculation, and layout and safety guidelines.
Telecom power supplies are specified for operation over a wide input-voltage range (36V to 75V) but with circuit performance optimized at 48V. Such circuit designs should be compact, efficient, and have a low profile to comply with the tight spacing between cards. This app note discusses a 5W flyback converter for telecom applications, based on the MAX5021 IC—a universal offline power-supply controller.
Telecom systems include numerous line cards. Connected in parallel to the high-power backplane, each has its own input-filter capacitor and low-voltage power converter. The large number of input-filter capacitors in parallel limits the value of each to a few microfarads, making the power-supply design fairly difficult.
The MAX5021 IC is a high-frequency, current-mode PWM controller suitable for wide-input-range, isolated telecom power supplies. It enables the design of small, efficient, power-converter circuits. A fixed-switching frequency of 262kHz controls switching losses while allowing moderately small power components. The IC includes undervoltage lockout capability with large hysteresis and a low startup current. This results in low-loss designs for power supplies that feature a wide input-voltage range and low output power. Cycle-by-cycle current limiting (achieved with a fastinternal comparator) reduces overdesign in the MOSFET and transformer. Other features include maximum-duty-cycle limiting and high-peak capability for the source and sink-drive currents. A reference design (Figure 1) illustrates the 5W flyback converter with an input-voltage range of 36V to 72V.

Figure 1. Based on the MAX5021 PWM controller, this flyback converter for telecom applications delivers 5W at 5V.
Power-stage Design
The first step in designing a power supply is deciding on a conversion topology. Topology selection criteria include the input-voltage range, output voltage, peak currents in the primary and secondary circuits, efficiency, form factor, and cost.
The best choice for a 5W output with a 1:2 input-voltage range and small form factor is a flyback topology whose minimum component count reduces the cost and form factor. The flyback transformer can be designed to operate either in continuous or discontinuous mode. Discontinuous mode causes the transformer core to complete its energy transfer during the off cycle, and continuous mode allows the next cycle to begin before the energy transfer is complete. In the present case, discontinuous mode is chosen for the following reasons: it maximizes energy storage in the magnetic component (thereby reducing the component's size); it simplifies compensation (no right-half-plane zero); and it yields a higher unity-gain bandwidth.
A disadvantage of the discontinuous operating mode is the higher ratio of peak-to-average current in the primary and secondary circuits. A higher ratio means higher RMS current, which leads to higher loss and lower efficiency. For low-power conversion, the advantages of discontinuous mode easily surpass the disadvantages. Moreover, the IC's drive capability is sufficient for driving the large switching MOSFET necessary to carry these peak currents. A telecom application using the MAX5021 in this topology easily achieves power outputs to 15W using standard MOSFETs.
Transformer Design
The key to low loss and high efficiency in the transformer is a proper core. The core and the winding-area product determine the amount of power the transformer can handle with an acceptable rise in temperature. Also considered in the core selection are the topology (ratio of average to RMS current in the winding), output current, efficiency, and form factor. The design of a discontinuous-mode transformer is explained below, step by step. Note that the first equation is a general one, and the second is specific to the MAX5021 power supply with a 40°C temperature rise.
- Estimate the minimum area-product requirement, and select a core and bobbin with suitable form factor.
- Calculate the secondary-winding inductance for guaranteed core discharge within the minimum off-time.
- Calculate the primary-winding inductance for sufficient energy to support maximum load.
- Calculate the number of turns in the primary.
- Calculate the number of turns in the secondary and bias windings.
- Calculate the AL value of the core.
- Calculate the RMS current in the primary, and estimate the secondary RMS current.
- Consider the proper winding sequence and transformer construction for low leakage.
1. Use the following equation to estimate the minimum area product required:

where:
 = expected efficiency of the converter;
= expected efficiency of the converter;
KP = area assigned to the primary (usually 0.5);
KT = ratio of RMS to average current in the primary (0.55 to 0.65 for discontinuous flyback);
KU = window utilization factor (0.4 to 0.5);
J = current density (9.862x106 A/m2, for winding temperature rise less than 40°C); and
BMAX = maximum-operating flux density in Teslas (use between 0.12T to 0.15T).
Select a core with area product (AP) equal to or greater than the figure calculated above, and note its core cross section area. Refer to the following table for output power vs. core size, AP, and core cross-section area (Ae):
Output Power vs. Core Size
| Output Power (W) | Core Size | AP (mm4) | Ae (mm2) |
| Up to 2 | EPC-10 | 30 | 9.4 |
| 3 to 4 | EEM-12.7 | 90 | 12 |
| 5 to 8 | EPC-13 | 145 | 12.5 |
| 9 to 12 | EFD-15 | 216 | 13.5 |
| (Refer to the Appendix for an example.) | |||
2. As discussed earlier, discontinuous operation requires that the core be discharged during the off-cycle. Secondary inductance determines the time required to discharge the core. Use the following equations to calculate secondary inductance:

where:
VD = secondary-diode forward-voltage drop in volts.
IOUT = maximum-rated output current in amperes.
3. Rising current in the primary builds energy in the core during the on-cycle, which is then released to deliver output power during the off-cycle. The primary inductance must hold enough energy during the on-time to support the maximum output power.

4. Next, calculate the primary number of turns necessary to keep the maximum flux density within limits at the maximum V-s product across the primary. The maximum-operating peak current occurs at the maximum duty cycle.

where:
Ae = core cross-section area in square meters.
5. Round off the primary number of turns to the closest integer, and calculate the number of turns for the secondary and bias windings using the rounded-off primary number of turns. Refer to the following equation:

The forward-bias drops of secondary- and bias-rectifier diodes are assumed to be 0.2V and 0.7V, respectively. Refer to the diode manufacturer's data sheet to verify these numbers. Again, round off the number of turns for secondary and bias windings to the closest integers.
6. The core's AL value depends on the air gap in the magnetic path length. Most of the energy is stored in the air gap during the MOSFET's on-time. To reduce electromagnetic radiation, insert the air gap in the center leg of the core.

7. The transformer manufacturer must know the RMS currents in the primary, secondary, and bias windings to decide the thickness of the wire. To keep skin-effect loss under control, only wires thinner than 28AWG are recommended. Multiple wires in parallel can be used to achieve the required copper thickness. Multifilar windings are very common in high-frequency converters. Maximum RMS current in the primary and secondary windings occurs at 50% duty cycles (minimum input voltage) and maximum output power. Use the following equations to calculate primary and secondary RMS currents:

Bias current is usually less than 10mA, so the selection of wire thickness depends more on the convenience of winding the wire than its current capacity.
8. The winding technique and sequencing is important in achieving a lower leakage-inductance spike at switch turn-off. As an example, interleave the secondary between two primary halves and keep the bias winding close to the secondary, so the bias voltage follows the output voltage.
MOSFET Selection
Selection criteria for the MOSFET include maximum drain voltage, peak/RMS current in the primary, and maximum-allowable power dissipation for the package (without exceeding the junction temperature limits). Voltage at the MOSFET drain is the sum of the input voltage, the secondary voltage reflected through the transformer turns ratio, and the leakage-inductance spike. (Figure 2 illustrates the relationship between drain voltage and primary current.) The MOSFET's absolute maximum VDS rating must be higher than the worst-case drain voltage (maximum input voltage and output load).

Figure 2. This scope photo shows Figure 1's circuit operating at VIN = 36V, VOUT = 5V, and IOUT = 1A. The switching MOSFET (Q1) exhibits drain voltage (upper trace) at 50V/div, and primary current (lower trace) at 0.65A/div.

A lower VDS Absolute Maximum Rating means a shorter channel, lower RDS(ON), lower gate charge, and a smaller package. Thus, it is advisable to keep VDS(MAX) low by choosing a lower NP/NS ratio and keeping the leakage-inductance spike under control. The resistor/capacitor/diode (RCD) snubber network can suppress such spikes.
The RMS current in the primary can be used to calculate DC loss in the MOSFET. Switching loss in the MOSFET depends on the operating frequency, the total gate charge, and the cross-conduction loss during turn off. Cross-conduction loss during turn-on is neglegible, because in discontinuous-conduction mode the primary current starts from zero. To avoid damage during power-on and during fault conditions, it may be necessary to derate the MOSFET. Use the following equation to estimate the MOSFET's power dissipation:

where:
QG = total gate charge of the MOSFET in coulombs;
VCC = bias voltage in volts;
tOFF = turn-off time in seconds;
cDS = drain-to-source capacitance in farads.
RCD Snubber-network Design
To avoid an excessive VDS requirement for the MOSFET, we recommend using an RCD snubber across the primary to suppress the spike caused by energy in the leakage inductance. The snubber dissipates energy that would otherwise dissipate in the MOSFET itself. The snubber capacitor's value should be high enough to absorb the leakage-inductance energy without allowing the MOSFET drain voltage to rise beyond an acceptable limit. Use the following equation to calculate this capacitance:

where:
LL = leakage inductance, which should be specified by the transformer vendor. (Values of 1µH to 3µH are common for the transformer under discussion.)
VSPIKE = spike voltage, typically 30V to 50V.
IPK = peak primary current, which in this case (for a worst-case spike) equals the current-limit threshold divided by RSENSE.
The diode must be a fast-switching type, with reverse-blocking voltage at least equal to the VDS(MAX) rating of the MOSFET. The resistor is selected for an RC time constant 2 to 3 times the switching period. Power dissipation in the resistor is the sum of the leakage inductance energy times frequency, plus the power loss caused by DC bias across the capacitor. The following equation lets you estimate power dissipation in the resistor:

where:
DMIN = minimum duty cycle = DMAX/2. (A 50% derating is recommended for chip resistors.)
Input Filter Design
The input filter reduces the amplitude of AC components in the converter's current pulses, thereby making the converter appear to the source as a DC load. Design parameters for this filter are the RMS ripple-current capability, input voltage, and the allowable level for AC components reflected back to the source.
Because discontinuous-mode flyback converters draw peak triangular currents through the capacitor ESR during each cycle, large aluminum electrolytic capacitors are needed for their low ESR and high ripple-current ratings. Unfortunately for a distributed power system, the input-filter capacitances of parallel converters add together and may produce an unacceptable inrush current at startup. As an alternative, you can use ceramic capacitors to achieve low ESR and a high ripple-current rating while keeping the total capacitance low.
The input peak-to-peak ripple voltage is a combination of the voltage drop due to capacitor ESR (ΔVESR) and the loss of charge from the capacitor (ΔVC). For low-ESR ceramic capacitors, use a 3:1 contribution from charge loss and ESR ripple respectively, and use the following equation to estimate capacitance and ESR for the capacitor:

Choose a capacitor that can handle the necessary RMS ripple without increasing its internal temperature (Figure 3). Use the following equation to estimate RMS ripple in the input capacitor:


Figure 3. This scope photo shows Figure 1's circuit operating at VIN = 72V, VOUT = 5V, and IOUT = 1A. The circuit exhibits input-voltage ripple at 500mV/div (lower trace), and drain voltage at 50V/div (upper trace).
Output Filter Design
The output capacitance required depends on the level of peak-to-peakb ripple acceptable at the load end. The output capacitor for flyback converters supports load current during the switch on-time. The transformer secondary replenishes those lost charges by discharging the core during the off-cycle, and simultaneously supplies the load current. Again, output ripple is the sum of the voltage drop due to the output capacitor's ESR (ΔVESR), and the charge loss (ΔVC) during the switch on-time. High switching frequency in the MAX5021 reduces the capacitance requirement. Use low-ESR tantalum capacitors for their favorable combination of capacitance and ESR, and use the following equations to calculate the capacitance and ESR:

where:
DOFF is the discharge duty cycle, calculated using the following
equation:

Additional noise spikes ride on the output ripple, caused by the di/dt of secondary current flowing through the output capacitor's ESL. A small LC filter can suppress these low-energy spikes, and it helps in attenuating switching-frequency ripple as well. To minimize the filter's effect on phase loss and ensure that it does not interfere with compensation, you should design its corner frequency more than one decade away from the estimated closed-loop bandwidth. Figure 4 shows the peak-to-peak ripple waveforms with and without the LC filter. Use a low-ESR ceramic capacitor of 1µF to 10µF, and calculate the inductance using the following equation:

where:
fC = estimated closed-loop bandwidth.

Figure 4. This scope photo shows Figure 1's circuit operating at VIN = 72V, VOUT = 5V, and IOUT = 1A. The circuit has less output-voltage ripple with an LC filter (lower trace at 100mV/div) than without (upper trace at 200mV/div).
Power Loss Consideration
High-frequency switching converters can be very lossy, since switching loss simply adds to the DC loss. Careful component selection is necessary to keep switching loss at a minimum. The MAX5021 is designed to operate at a sufficiently high frequency to reduce the size of passive components while minimizing switching losses. The MAX5021's low startup current and low-quiescent operating current minimize power loss in the control circuitry. To reduce switching loss even further and achieve higher converter efficiency, use a MOSFET with low gate charge and low gate-to-drain capacitance, and balance the MOSFET's DC and switching-power losses. See graph of Converter Efficiency vs. Output Current (Figure 5), and use the following equation to calculate DC and switching losses in MOSFET:

where:
QG = total gate charge for the MOSFET in nanocoulombs;
VCC = voltage at VCC (pin 4 of MAX5021);
tf = turn-off time in seconds;
VD = drain voltage at turn-off in volts;
fSW = switching frequency (262kHz);
iPK = primary peak current in amperes.

Figure 5. The graph demonstrates Efficiency vs. Output Current curves for the circuit in Figure 1.
Use a Schottky diode in the secondary to achieve low VDS and low reverse-recovery loss. Use the following equation to calculate DC loss in the secondary diode while neglecting reverse-recovery loss due to switching:

where:
VFB = forward drop for the secondary diode at ISPK/2, in volts.
You can reduce the transformer-leakage inductance between primary and secondary by sandwiching the secondary between two halves of the primary. Use a multifilar winding structure to reduce skin-effect loss.
Frequency Compensation
The absence of a right-half-plane (RHP) zero in the discontinuous flyback converter simplifies the closed-loop frequency compensation to a single pole-zero pair. No bandwidth limit arises from the location of the RHP zero. The loop is closed through the shunt regulator, optocoupler, and PWM comparator internal to the MAX5021. The location of the error amplifier's pole and zero is determined from the existing PWM gain, the output-filter pole, and the ESR zero frequency. Use the following equations to calculate the current-mode converter's PWM gain, the output-capacitor filter pole, and the output capacitor's ESR zero:

Capacitor filter pole (fP):

Capacitor ESR zero (fz):

where:
RL = load resistance;
CTR = current-transfer ratio of optocoupler;
R = current-sense resistor in the primary path; and
= current-sense resistor in the primary path; and
CO = output-filter capacitor.
Total loop gain equals the PWM gain (APWM) times the gain of the voltage divider and the error amplifier (shunt regulator). The available worst-case phase margin (PM) occurs at full load.
The response of the combined-error amplifier, optocoupler and PWM is too complicated to estimate analytically. You should therefore use the existing compensation network to plot a Bode diagram of the closed-loop transfer function from control to output. Then place the zero and pole at appropriate locations for maximum "phase bump" at the crossover frequency. To maintain a gain slope of -1 to well beyond the crossover frequency, place the error-amplifier pole at the ESR zero location. Use the following equations to calculate the zero (fZE) and poles (fPE) of the error amplifier:

Optimization on the board produces a closed-loop bandwidth of 8kHz with 44° of phase margin. The Bode plot of Figure 6 is based on the circuit of Figure 1, with values as shown for the compensation components.

Figure 6. This Bode plot illustrates stability for the Figure 1's circuit operating with component values as shown.
We can verify the load-transient response for a small-deviation, fast-settling perturbation in the output voltage by switching the load from 100mA to 1A in 20µs (Figure 7). An overcompensated converter increases the response time, which may also cause an output overshoot during turn-on. Figure 8 depicts the result of an optimally compensated loop.

Figure 7. The transient response for the Figure 1's circuit: IOUT at 1A/div (lower trace), and VOUT at 100mV/div (upper trace).

Figure 8. These startup waveforms appear in the Figure 1's circuit with an optimally compensated loop. The circuit has 48V input voltage at 20V/div (lower trace), and 5V output voltage with 1A load at 2V/div (upper trace).
Layout and Safety Guidelines
High-frequency switching converters produce current and voltage waveforms with high slew rates. To minimize voltage spikes and electromagnetic radiation, you should minimize inductance in the current loops and PC traces. Component placement is critical in keeping the high-frequency traces short. Follow the steps below for good layout:
- Minimize the loop formed by the input capacitor positive terminal, transformer primary, MOSFET switch, current-sense resistor, and input-capacitor negative terminal.
- Keep the gate-drive trace from the MAX5021 to the switching MOSFET short.
- Place the RCD snubber components close to the input capacitor and MOSFET switch.
- Place the ceramic capacitors connected to the MAX5021 VCC, VIN, and CS pins close to the IC.
- Minimize the loop formed by the transformer secondary, secondary diode, and output capacitor.
- For effective heatsinking on the PC board, connect a large copper area to the MOSFET drain, transformer secondary, and secondary diode.
The type of circuit (SELV, TNV-1, TNV-2, or TNV-3) and its degree of pollution (determined by the circuit surroundings) determine the requirements for clearance and creepage between the primary and secondary circuits. For the minimum clearance and creepage distances between different circuit components, contact your safety engineer or refer to Underwriters Laboratory standard UL60950.
Appendix - Transformer Design
Given the specifications VIN = 36V to 72V, VOUT = 5.1V, and IOUT = 1.1A, proceed as follows:
Step 1. Area product (AP):

Select EPC13 (TDK Part Number ? PC44EPC13-Z)
Core Ap and Ae:

Step 2. Secondary inductance (LS):
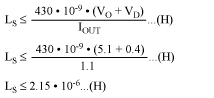
Step 3. Primary inductance (LP):

Step 4. Primary turns (NP):

Round off the primary turns, NP = 48t.
Step 5. Secondary- and bias-winding turns (NS and Nbias):

Round off the secondary turns, NS = 9t:

Round off the bias-winding turns, Nbias = 20t.
Step 6. Value of the core:

Step 7. Primary and secondary RMS currents (IPRMS and ISRMS):





















