Choosing the MAX1932 External Inductor, Diode, Current-Sense Resistor, and Output Filter Capacitors for Worst-Case Conditions
The MAX1932 is a boost converter controller targeted for avalanche photodiode (APD) bias supplies in medium to long reach optical communication networks. Although the MAX1932 can operate in either continuous or discontinuous conduction mode, due to the high ratio of output voltage to input voltage for an APD bias application and high-switching frequency, discontinuous conduction mode boost topology is chosen. This application note describes the fixed-frequency discontinuous conduction mode boost topology and shows how to select the inductor, diode, and output filter capacitors for worst-case conditions.
Discontinuous mode means that there is an interval during a switching cycle where the inductor current is zero. Refer to the schematic of Figure 1 and the associated waveforms of Figure 2. At the beginning of each switching cycle, the MOSFET (Q1) turns on, thus applying the input voltage across the inductor (L1). The inductor current ramps up from zero to a peak value (IL1_PK) required to store enough energy to support the output. This stored energy will be completely released to the output via diode D1 prior to the end of Q1 off time, where the inductor current decays to zero.
The energy stored and released by the inductor L1 every switching cycle is:
ES = 0.5L1 × (IL1_PK)²
At the switching frequency, fS, the power released from the inductor is then:
PL1 = ES × fS = 0.5L1 × (IL1_PK)² × fS
This power is equal to the maximum output power plus any power losses in the circuit.
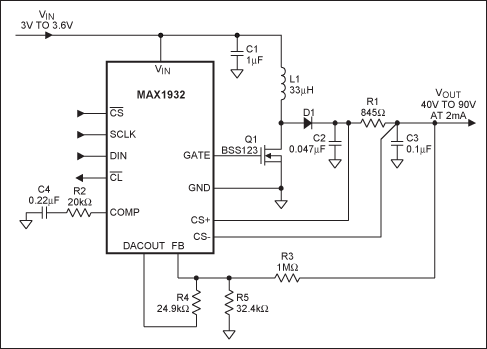
Figure 1. Typical application circuit for 3V to 3.6V input, 40V to 90V output at 2mA.
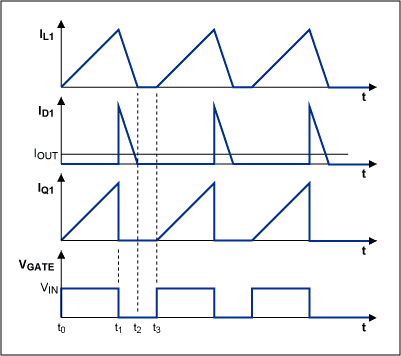
Figure 2. Waveforms of inductor current (IL1), diode current (ID1), MOSFET switch current (IQ1), and gate voltage (VGATE).
This can be expressed by the equation below:
0.5L1 (IL1_PK)² × fS = PO_MAX/η = VO_MAX × IO_MAX)/η
Where η is the efficiency of the circuit, taken into consideration of the power losses as mentioned above.
The value of the peak inductor current is a function of the input voltage, the operating duty cycle, D, and the switching frequency:
IL1_PK = (VIN × D)TS/(L1)
Where TS = 1/fS, the switching period.
Substituting IL1_PK of (4), into (3), and solve for L1:
L1 = ((VIN × D)² × TS × η)/(2 × VO_MAX × IO_MAX)
To ensure that under worst-case voltage conditions and component tolerances, the value of L1 must meet the requirement below:
L1MAX = ((VIN_MIN × DMAX)² × TS_MIN × ηMIN)/(2 × VO_MAX × IO_MAX)
Since TS_MIN = 1/fS_MAX, then:
L1MAX = ((VIN_MIN × DMAX)² × ηMIN)/(2 × VO_MAX × IO_MAX × fS_MAX)
Where DMAX is the maximum duty cycle at the highest switching frequency.
For the MAX1932, select DMAX of 0.85 to allow about 5% margin from the data sheet typical specification. The value of ηMIN can be set at 0.70 as a starting point, for calculating the inductor value. Since low-cost commercial inductors can have tolerance in the range from, ±10% to ±20%, make sure that with worst-case tolerance the inductor value does not exceed L1MAX. For example with ±10% tolerance, the nominal inductance value is then:
L1 = L1MAX/1.10
The calculated inductance value should be verified with test results, and a final tweak to the calculated value can be made if deemed necessary. The value calculated was based on worst case when the switching frequency is at maximum value, as specified in the MAX1932 data sheet. At any other switching frequency in the specified range, and at VIN_MIN, VO_MAX, IO_MAX the measured operating duty cycle should not exceed DMAX(fS) below:
DMAX(fS) = DMAX(fS/fS_MAX)1/2 = 0.85(fS/340kHz)1/2
Where fS_MAX is the maximum switching frequency of 340kHz, due to the tolerance of the internal oscillator of the MAX1932.
If the measured operating duty cycle is higher then DMAX(fS), then the efficiency η is probably lower than the 0.70 assumed as a starting point. In this case the value of the inductor needs to be lowered. If the measured duty cycle is less than DMAX(fS), the circuit will work under all worst-case conditions. However if it is much lower then the required DMAX(fS), it is undesirable, since this would result in unnecessary higher peak current that would degrade the efficiency. It is suggested to have the operating duty cycle in the range of 0.95 × DMAX to DMAX. To increase the operating duty cycle, raise the inductance value.
Once the inductor value is determined, the maximum peak operating steady state inductor current is:
IPK_MAX = VIN_MIN × DMAX × (fSMIN/fS_MAX)1/2/(fS_MIN × LMIN)
Note that under an output step load transient, the maximum peak inductor current can momentarily be higher, and the absolute maximum value is:
IPK_TMAX = (VIN_MAX × DMAX)/(fS_MIN × LMIN)
Make sure that the inductor does not saturate at this maximum peak transient current.
The time required for the inductor current to ramp up from zero to IPK_MAX (t1–t0 in Figure 2) is:
TRUP = IPK_MAX × LMIN/VIN_MIN
The time requires to ramp down from the IPK_MAX above to zero (t2–t1 in Figure 2) is:
TRDWN = (VIN_MIN × TRUP)/(VO_MAX - VIN_MIN)
The maximum average inductor current is:
IL1_AVG = 0.5IPK_MAX × (TRUP + TRDWN) × fS_MIN
The inductor current flows through the MOSFET during the ramp-up interval, and through the diode, D1, during the ramp-down interval. Hence, the maximum RMS current through the FET is:
IQ1_RMS = IPK_MAX (TRUP × fSMIN/3)1/2
And the diode average current is:
ID1_AVG = 0.5IPK_MAX × TRDWN × fS_MIN
For most APD bias supply application, the average diode current is less than 5mA, therefore a small Schottky or silicon switching diode can be used. Ensure that the Q1, D1, C2 and C3 voltage rating are sufficiently higher than the maximum output voltage.
Ceramic capacitors have low equivalent series resistance (ESR) and inductance (ESL) at high frequency, with low capacitance value for small size and low cost. They are recommended for output filtering. For the circuit of Figure 1, in addition to the typical output filter capacitor, C2, there is a lowpass filter formed by R1 and C3 to further reduce the switching ripple to a very low level to bias the APD diode. The peak-to-peak ripple voltage across C2 is comprised of the ripple due to its ESR, ESL and the capacitance charge displacement. The three ripple components are additive and superimpose on each other to yield the total worst-case peak-to-peak ripple voltage at C2 of:
VC2_RPL = (IPK_MAX × ESR) + (VO_MAX - VIN_MIN) × (ESL/L1) +
[IO_MAX × ((1/fS_MIN) - TRDWN)/C2]
The resistor R1 serves two purposes, as a current-sense resistor for cycle to cycle current limit and as part of an RC lowpass filter to attenuate the switching ripple voltage. The value of R1 is chosen so that the voltage drop across R1 at maximum output current and ripple voltage does not trip the minimum current limit threshold of 1.8V. Hence R1 can be calculated as:
R1 = (1.8V - 0.5VR1_RPL)/IO_MAX
Where VR1_RPL is the peak-to-peak ripple voltage across R1, and can be expressed as:
VR1_RPL = VC2_RPL [1 - (1/( 2 × π × R1 × C3 × fS_MIN))]
Solving for R1 from (18) and (19) yields:
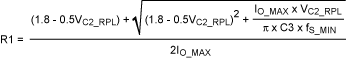
The worst-case output peak-to-peak ripple voltage, VO_RPL, is then :
VO_RPL = VC2_RPL/(2 × π × R1 × C3 × fS_MIN)
As seen from (21), the output ripple voltage is inversely proportional to the value of R1 and C3. However the value of R1 is bounded by the current limit circuit as shown in (20), while the value of C3 is only limited by its size and cost.
Since ceramic capacitors have very low ESR and ESL, the ripple voltage across C2 as expressed in (17) is mostly caused by the capacitor's value. Therefore, we can say that the output ripple voltage is also inversely proportional to the value of C2. Similar to C3, the value of C2 is only limited by its size and cost.
Make sure that the value of C2 and C3 are large enough to cover their tolerances and variation due to temperature.
Below is a design example using the above equations:
VIN: 3V (min), 3.6V (max)
VO: 40V (min), 90V (max)
VO_RIPPLE: < 1.5mVP-P
IO: 2mA (max)
fS: 250kHz (min), 340kHz (max)
C2 = 0.047µF, ESR = 5mΩ, ESL = 1nH
C3 = 0.1µF
First, select DMAX = 0.85 and ηMIN = 0.70, calculate L1MAX per (7) above:
L1MAX = 37.19µH
For ±10% tolerance, the nominal L1 value is:
L1 = 37.19µH/1.1 = 33.8µH
Use a standard inductor value of 33µH. Hence, L1MIN = 0.9 × 33µH = 29.7µH
Now, calculate the worst-case maximum peak steady state and transient inductor current using (10) and (11):
IPK_MAX = 294mA (peak) and IPK_TMAX = 412mA (peak)
From (12), (13), and (14), the average inductor DC current is:
IL1_AVG = 111mA
Note that the currents above only occur when the switching frequency and inductor are at minimum value due to tolerances. As mentioned above, select the inductor with the rated saturation current above 353mA.
From (12) and (15), the RMS current of Q1 is:
IQ1_RMS = 145mA
From (13) and (16), the average current of D1 is:
ID1_AVG = 3.7mA
From (17), (18), (19), and (20), the value of the current-sense and filtering resistor, R1, is:
R1 = 856.5Ω
Select 845Ω, 1%, the next standard value lower than the 856.5Ω calculated. From (17), and (21), the worst-case output peak-to-peak ripple voltage is:
VO_RPL = 1.28mVP-P
As previously stated, the value of C2 and C3 can be increased to further reduce the output ripple. For example, doubling the value of C2 or C3 will cut the output ripple in half.
It has been shown how to select the inductor (L1), diode (D1), current-sense resistor (R1), and filter capacitors (C2 and C3) to meet the output voltage, output current and ripple requirement for worst-case conditions that include input voltage, switching frequency variation, current-limit-threshold variation.




















