要約
Of all the low-frequency oscillator configurations, the Wien bridge is the easiest to use. It is reliable, uses standard components, gives a good sine wave, and is fairly immune to the type of op amp around which it is designed. A Wien bridge can, however, be misunderstood and oversimplified, leading to designer frustration. This article describes the theory and practicalities of using a Wien-bridge oscillator, and how to make the circuit more stable and more factory-/user-flexible.
The Wien-Bridge Oscillator Circuit
The circuit of a standard Wien-bridge oscillator is shown in Figure 1.
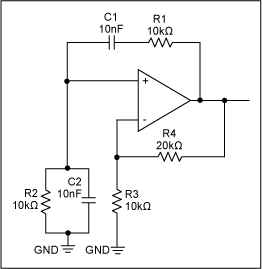
Figure 1. A standard Wien-bridge oscillator circuit.
A circuit maintains oscillation when the loop gain at the frequency of oscillation is unity, and the phase shift of the feedback signal at the frequency of oscillation is zero or a multiple of 2π.
First, the phase shift needs to be considered. In Figure 1, R1 and C1 produce a positive phase-shifted current with respect to the output voltage. When this phase-shifted current meets R2 and C2, these latter components produce a negative phase-shifted voltage. At a specific frequency, the phase shift caused by R1 and C1 is offset by an equal and opposite phase shift caused by R2 and C2, so the net phase shift is zero. When this occurs, the circuit is in danger of oscillating.
Next, we consider the transfer function of the network comprised of R1, C1, R2, and C2. Because the op amp's output impedance is low and its impedance at both inputs is very high, determining the transfer function of the Wien network (i.e., the resistive divider made up of R1 and C1 on the top and R2 and C2 on the bottom) is relatively straightforward. Thus, the transfer function is:
The transfer function is:

Where j represents a 90-degree phase shift in the transfer function (either positive or negative). The other (non-"j") terms represent a zero phase shift in the transfer function. As the magnitude of the terms change, the resultant phase shift also changes. Equation 1 shows that the "non-j" terms in the denominator equal zero, leaving only j terms in the numerator and denominator.
Dividing the numerator and denominator by jw leaves no j terms and, hence, no phase shift. Therefore, the condition for zero phase shift at a given frequency is calculated in Equation 2.

Next, one must consider the gain. Once the terms in Equation 1 are resolved and the resonant frequency is determined, the transfer function is:

To simplify this, it is wise to equate R1 to R2 and C1 to C2. It can then be seen that at resonance, the transfer function from output to input is:

To meet the requirements of oscillation (i.e., zero phase shift and unity gain), the op amp circuit needs to have a gain of 3 to overcome the attenuation resulting from the Wien-bridge network. From another perspective, to keep the two op amp inputs at the same voltage, the resistor network from the output to the inverting input needs to provide an attenuation of 3 to match the attenuation of the Wien network.
In theory, this technique is very convenient but it is not practical. Low tolerance resistors are easily included in a design. Finding accurate capacitors is, however, more difficult, and including capacitors with an accuracy greater than 20% can be costly. Therefore, it is wise to consider the effect of different capacitor values on the performance of the circuit.
Figure 2 shows a simple spreadsheet illustrating the values of the Wien-bridge network and their impact on the gain. Cell B7 is the transfer function represented in Equation 3, cell B12 is determined in Equation 2 (with the answer in kHz), and cell B9 is the reciprocal of cell B7. If C1 = C2 = 10nF and R1 = R2 = 10kΩ, the circuit oscillates at 1.59kHz with an op amp gain equal to 3. A practical measurement of this circuit supports this calculation.
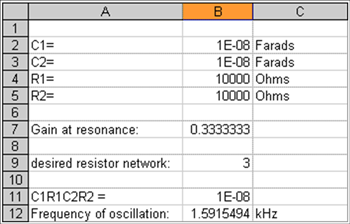
Figure 2. Example of Wien-bridge component values.
However, the above results were achieved with ±10%-tolerant capacitors. A quick inspection of a components catalogue shows very similar capacitors designed for decoupling that exhibit a tolerance of -20%/+80%. In this case, with C1 = 8nF (10nF -20%) and C2 = 18nF (10nF + 80%), the circuit requires a gain of 4.25. Inserting these components into the design causes the circuit's gain to be insufficient (it only delivers a gain of 3). The circuit, therefore, does not oscillate. Alternatively, if C1 is high and C2 is low, the circuit has too much gain and oscillates, but with significant distortion. Also, once the circuit is oscillating, the frequency is incorrect due to the wide tolerance of the capacitor values. The ideal circuit is one that is just biased to the point of oscillation. Any less gain and the circuit stops oscillating; any more gain and it starts to distort.
A JFET in the feedback network, as illustrated in Figure 3, solves this problem. With the JFET, the gain can vary over a small range to ensure consistent oscillation. At startup, the JFET gate voltage is zero; therefore, the drain-source impedance is very low. This design produces a gain greater than 3 (to get the circuit going). Once oscillations build up, the rectified negative transitions of the output provide a turn-off voltage for the JFET's gate. This reduces the gain, and the circuit settles down to stable oscillation. The amplitude of the output depends on the voltage drop across the two diodes, as well as the turn-off voltage of the JFET. Unfortunately, JFETs have a large variation in gate turn-off voltage, which causes the circuit's output voltage to vary considerably from batch to batch. TR1 was selected because it has a very low variation of gate turn-off voltage, thus guaranteeing a small variation in output voltage from circuit to circuit. But this TR1 circuit often does not yield the lowest distortion oscillator. In fact, the circuit oscillates, but with significant distortion; the JFET maintains this oscillation regardless of the distortion. Therefore, the JFET should only be used as an aid to keep the circuit going, not to compensate for poor circuit design.

Figure 3. A Wien-bridge oscillator with a junction gate field-effect transistor (JFET) in the feedback network.
Unless complex circuit design can be tolerated, the simplest way to ensure that the circuit starts up and continues to oscillate without distortion (due to too much gain) is to insert a variable resistor in the feedback path. The resistor is then adjusted to the point where the circuit just starts to oscillate. This provides a clean sine wave with the lowest distortion.
Although some engineers consider a variable resistor a simple design solution, manufacturing engineers see them as a time-consuming production headache. It takes time and manpower to adjust a variable resistor, making the circuit complex and expensive to produce.
The ideal solution to this dilemma is to insert an electronically variable resistor or digital potentiometer (digipot). In Figure 3, replacing the variable resistor VR1 with a digipot provides a low-cost, small, simple solution that enables the circuit to be adjusted during production to ensure minimal distortion. This digipot can be used alone or with other resistors, either in series or parallel, to fine-tune the gain. Once the circuit is oscillating, the JFET provides the fine gain modifications that keep the circuit going.
In the circuit shown in Figure 3, the MAX5467 10kΩ digipot can be substituted for the variable resistor VR1. Because this part has two floating terminals, it does not have to be ground referenced. Inserting additional MAX5467 parts in series with R1 and R2 enables the user to adjust the frequency of the circuit. The digipots' simple digital interface means that the circuit can be manually adjusted without needing a microcontroller.
With the two 10kΩ digipots inserted in series with resistors R1 and R2, the circuit's operating frequency can be adjusted from 833Hz to 1.6kHz. Also, once the 10kΩ digipot is inserted in place of VR1, the circuit's output can be adjusted electronically from DC to pure sine wave and to distorted sine wave as the gain of the circuit changes.
Figure 4 shows the final circuit including the MAX5467 digipot. Figure 5 shows an AC ground and a JEFT bias circuit. Figures 6 and 7 show frequency- and gain-adjust circuits, respectively. The digipots are represented by the symbols IC2, IC3, and IC4. IC2 and IC3 share the same digital interface and, hence, can be incremented and decremented simultaneously. IC4 provides an independent gain-adjust circuit.
To further linearize the characteristics of the JFET, two 100kΩ resistors were added around the gate. These resistors provide some negative feedback to the JFET and thus smooth out the nonlinearities of the JFET's performance.

Figure 4. A Wien-bridge oscillator with a JFET and a digipot in the feedback network.

Figure 5. An AC ground and a JFET bias circuit.
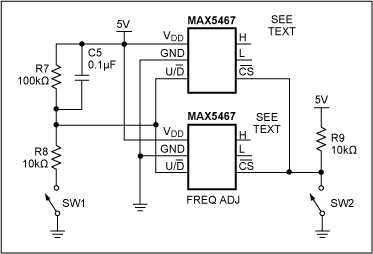
Figure 6. A frequency-adjust circuit using the MAX5467.

Figure 7. A gain-adjust circuit using the MAX5467.
Further Experiments
This article describes an analysis of the essential points of the Wien-bridge oscillator and the fundamentals of many oscillator designs. Without getting the basics correct, any circuitry added around the Wien bridge would only disguise mistakes.
However, improvements can be made by examining the circuit more closely and adding extra circuitry to further improve the performance.
The feedback loop can cause distortion. The diode forward voltage drifts with temperature (2.1mV/°C). This directly affects the output voltage. In addition, the JFET bias voltage changes with temperature. These voltage drifts can be overcome by adding an RMS-to-DC converter or a peak-level detector to the output. Such a circuit needs to produce an accurate DC output voltage that is proportional to the sine-wave output. If this DC signal is inverted (using a simple op amp circuit) and fed directly to the JFET input, the sine-wave output can be made more stable.
Conclusion
The Wien-bridge oscillator is easy to understand in theory, but the practicalities of the circuit can cause the designer frustration. Insertion of a digipot in three critical areas of the circuit ensures much more stable operation and factory/user adjustability.




















