• 3 2019
    VOL 53

「ADALM1000」で、SMUの基本を学ぶトピック15：インピーダンスの測定、周波数の影響

Doug Mercer, Antoniu Miclaus 共著 PDFをダウンロード

目的

今回の実験の目的は以下の2つです。

  1. インピーダンス・アナライザ・ソフトウェア「ALICE Vector Voltmeter（ALICE-VVM）」を使って、部品のインピーダンスと回路のインピーダンスを測定します。
  2. 周波数の変化に応じて、RLC（抵抗、インダクタ、コンデンサ）回路のインピーダンスの大きさと位相がどのように変化するのか理解します。

背景

インピーダンスとは、交流電流に対する抵抗値のことです。特定の周波数において、回路全体が電流に対して示す抵抗値だと表現することもできます。インピーダンスZは、抵抗RとリアクタンスXの組み合わせとして表わされ、Ωを単位とする値として測定されます。インピーダンスZは、次式のような複素数として表わせます。

数式 1

インピーダンスは、実軸Xと虚軸Yを使用する2D（2次元）の極座標にプロットすることができます。抵抗成分は実軸上の線、リアクタンスの成分は虚軸上の線として表されます。

抵抗のインピーダンスはDC抵抗値と同じであり、X軸上の線となります。コンデンサのインピーダンス（より厳密に言えばリアクタンス）XCは虚数であり、2Dの極座標プロットでは、Y軸上で負の方向の線として表されます。コンデンサのリアクタンスは、周波数に依存して次の式のように変化します。:

数式 2

ここで、角周波数ω = 2πfです。

インダクタのインピーダンス（より厳密に言えばリアクタンス）XLも虚数であり、2Dの極座標プロットでは、Y軸上で正の方向の線として表されます。インダクタのリアクタンスも周波数に依存して次式のように変化します。

数式 3

RLC直列回路のインピーダンスは、各部品のインピーダンスの和になります。

数式４ｂ

上の式は、以下のように書き換えることもできます。

数式４ａ

また、インピーダンスは、極座標プロット上で位相ベクトル（フェーザ）として表すことも可能です。

数式 5
図1 . インピーダンス測定の対象とするRLC直列回路
図1 . インピーダンス測定の対象とするRLC直列回路
図2 . インピーダンス・アナライザの実行画面。RLC直列回路の測定結果を表示しています。
図2 . インピーダンス・アナライザの実行画面。RLC直列回路の測定結果を表示しています。

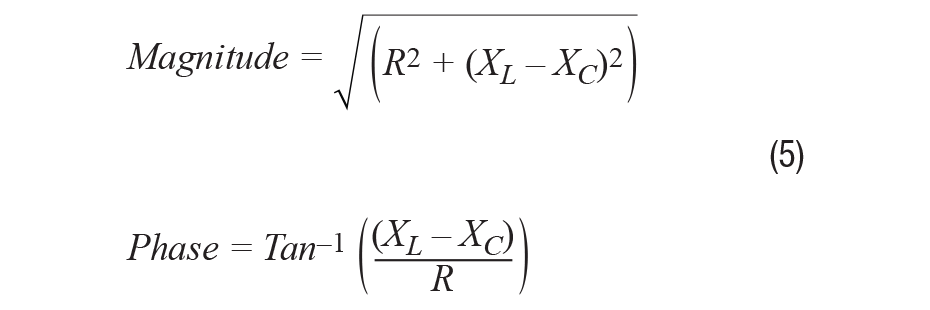
準備するもの

  • ADALM1000（アクティブ・ラーニング・モジュール）
  • 抵抗：1.0kΩ、470Ω
  • コンデンサ：1.0µF
  • Inductor (10 mH)

手順

  1. 各部品のインピーダンス測定

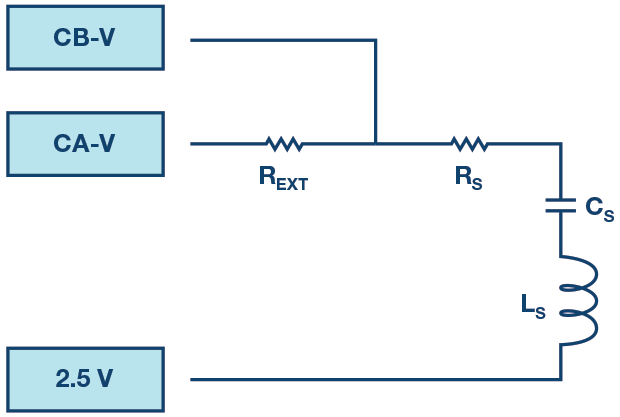
    1. 「CA-V」と「CB-V」の間に1kΩの抵抗REXTを接続し、「CB-V」と2.5Vの固定電源の間にRSとして470Ωの抵抗を接続します。
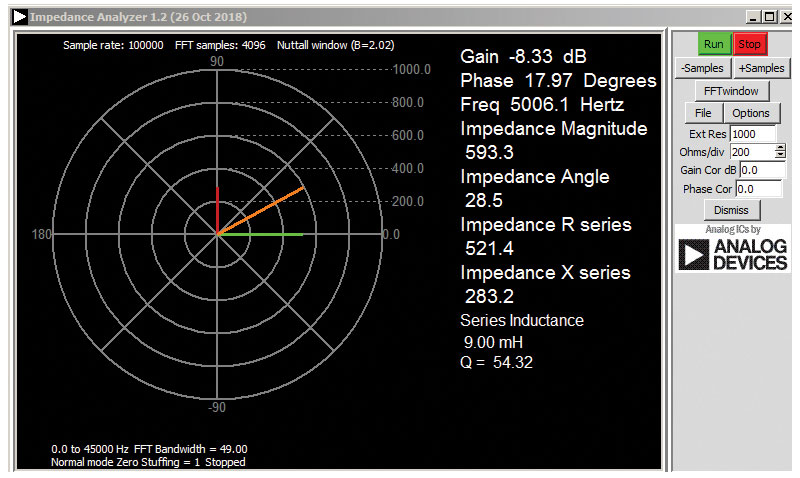
    2. ALICE-VVMを実行します。
    3. 表1に、この抵抗の振幅、位相、抵抗値、リアクタンスの測定値を記録します。なお、デフォルトの周波数は1000Hzに設定されていることに注意してください。プロットを見ると、フェーザが実軸上にあり、位相がゼロであることを確認します。また、リアクタンスはゼロであるため、振幅は抵抗値と同じになっているはずです。
    4. RSをCS（1.0µF）に置き換えて、振幅、位相、抵抗値、リアクタンスを測定します。得られた結果は表1に記録します。コンデンサのフェーザは虚軸上の負の側にあり、位相は270°または-90°になっているはずです。
    5. CSをLS（20mH）に置き換えます。振幅、位相、抵抗値、リアクタンスを測定し、得られた結果を表1に記録します。インダクタのフェーザは虚軸上の正の側にあり、位相は90°になっているはずです。
  2. RLC回路のインピーダンス測定、周波数が回路に及ぼす影響

    1. REXT（1kΩ）、RS（470Ω）、CS（1.0µF）、LS（20mH）を使って図1に示したRLC直列回路を構成します。
      図3 . ブレッドボード上に構成したRLC回路。この回路のインピーダンスを測定します。
      図3 . ブレッドボード上に構成したRLC回路。この回路のインピーダンスを測定します。
    2. デフォルトの周波数である1000Hzにおいて、RLC回路の振幅、位相、リアクタンス、抵抗値を測定します。得られた値を表1に記録します。
    3. 位相がゼロになるまで周波数を調整します。そして、その周波数の値を記録します。これは総リアクタンスがゼロになる特別な周波数であり、回路は純粋な抵抗性を示します。

      数式 6

      上の式において、以下の条件が成り立つとします。

      数式 7

      その場合、以下のような状態になるということです。

      数式 8

      つまり、RLC回路のインピーダンスが抵抗成分だけになるということです。この条件が成立する周波数を共振周波数と呼びます。共振周波数は、以下の式を使って数学的に求められます。

      数式 9
    4. fOより低い範囲で周波数を100Hzステップで変化させ、インピーダンス・アナライザを使って3つの測定値を取得します。それらの値を表1に記録します。続いて、fOより高い範囲で周波数を100Hzステップで変化させて、同じことを繰り返します。フェーザの振幅（橙色の線）が回転する様子を注意深く観察してください。

測定結果

表1. RLC回路に対する周波数の影響
周波数〔Hz〕 振幅〔Ω〕 位相〔°〕 抵抗〔Ω〕 リアクタンス
         
         
         
         
         

問題

  1. 式9を使ってRLC直列回路の共振周波数fOを算出し、それを測定値と比較してください。2つ値の差をパーセンテージで表すと、どのようになりますか。
  2. リアクタンス成分の値が抵抗成分の値と等しくなるときのRLC直列回路の振幅と位相を算出してください。

You can find the answers at the StudentZone blog.

注記

アクティブ・ラーニング・モジュールを使用する記事では、本稿と同様に、ADALM1000に対するコネクタの接続やハードウェアの設定を行う際、以下のような用語を使用することにします。まず、緑色の影が付いた長方形は、ADALM1000が備えるアナログI/Oのコネクタに対する接続を表します。アナログI /Oチャンネルのピンは「CA」または「CB」と呼びます。電圧を印加して電流を測定するための設定を行う場合、「CA-V」のように「-V」を付加します。また、電流を印加して電圧を測定するための設定を行う場合には、「CA-I」のように「-I」を付加します。1つのチャンネルをハイ・インピーダンス・モードに設定して電圧の測定のみを行う場合、「CA-H」のように「-H」を付加して表します。

同様に、表示する波形についても、電圧の波形は「CA-V」と「CB-V」、電流の波形は「CA-I」と「CB-I」のように、チャンネル名とV（ 電圧） 、I（ 電流）を組み合わせて表します。

著者

Doug Mercer

Doug Mercer

Doug Mercerは、1977年にレンセラー工科大学で電気電子工学の学士号を取得しました。同年にアナログ・デバイセズに入社して以来、直接または間接的に30種以上のデータ・コンバータ製品の開発に携わりました。また、13件の特許を保有しています。1995年にはアナログ・デバイセズのフェローに任命されました。2009年にフルタイム勤務からは退きましたが、名誉フェローとして仕事を続けており、Active Learning Programにもかかわっています。2016年に、レンセラー工科大学 電気／コンピュータ／システム・エンジニアリング学部のEngineer in Residenceに指名されました。

Antoniu Miclaus

Antoniu Miclaus

Antoniu Miclausは、アナログ・デバイセズのシステム・アプリケーション・エンジニアです。アカデミック・プログラムや、Circuits from the Lab®向けの組み込みソフトウェア、QAプロセス・マネジメントなどに携わっています。2017年2月から、ルーマニアのクルジュナポカで勤務しています。クルジュナポカ技術大学で電子工学と通信工学の学士号、バベシュボヨイ大学でソフトウェア・エンジニアリングの修士号を取得しています。